Індивідуальне завдання №1 2 страница
оскільки згідно із (2.13)
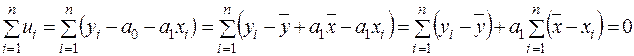 .
.
Відмітимо, що рівність (2.21) відповідає передумові 1 і вона виконується, взагалі кажучи, тільки у випадку 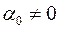 (пропонується самостійно переконатися в цьому).
(пропонується самостійно переконатися в цьому).
Отже, в оцінці 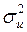 фігуруватиме тільки складова
фігуруватиме тільки складова 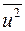 . Наступний крок — відкоригувати цю оцінку з тим, щоб вона стала незміщеною. Можна довести ([4, с.207]), що
. Наступний крок — відкоригувати цю оцінку з тим, щоб вона стала незміщеною. Можна довести ([4, с.207]), що 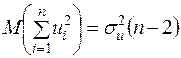 .
.
Тому
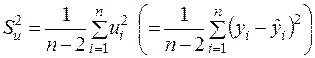 (2.22)
(2.22)
є незміщеною оцінкою невідомої 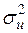 .
.
Звернемо увагу на знаменник у (2.22). Виникає питання, як його пояснити, враховуючи, що незміщеною оцінкою (виправленою дисперсією) невідомої генеральної дисперсії кількісної ознаки 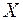 є
є
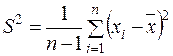 , (2.23)
, (2.23)
тобто знаменник у цьому випадку вже дорівнює 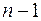 . Справа у тому, що для знаходження (2.23) вхідною інформацією є
. Справа у тому, що для знаходження (2.23) вхідною інформацією є 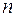 чисел
чисел 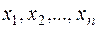 . Але серед чисел
. Але серед чисел 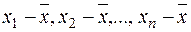 незалежними є тільки
незалежними є тільки 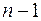 , оскільки
, оскільки 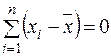 , тобто одне із чисел
, тобто одне із чисел 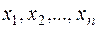 можна виразити з допомогою останньої рівності через решту
можна виразити з допомогою останньої рівності через решту 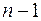 чисел.
чисел.
У випадку (2.22) вхідною інформацією є 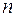 чисел
чисел 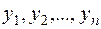 , які задовольняють двом рівностям (2.14). Тепер уже два числа можна виразити через решту, використавши ці рівності, тобто лінійно незалежними є вже
, які задовольняють двом рівностям (2.14). Тепер уже два числа можна виразити через решту, використавши ці рівності, тобто лінійно незалежними є вже 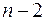 чисел.
чисел.
Число 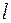 (для (2.22)
(для (2.22) 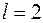 , а для (2.23)
, а для (2.23) 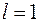 ) називається числом зв’язків, накладених на вибірку, при знаходженні дисперсії.
) називається числом зв’язків, накладених на вибірку, при знаходженні дисперсії.
Число 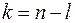 називається числом ступенів вільності.
називається числом ступенів вільності.
5. Згідно із (1.7) та (2.22) випадкова величина
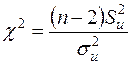 (2.24)
(2.24)
розподілена за законом 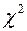 із числом ступенів вільності
із числом ступенів вільності 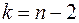 . Оскільки розподіл
. Оскільки розподіл 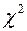 несиметричний [3, с.126], то це приводить до несиметричності і довірчого інтервалу для випадкової величини, розподіленої за цим законом.
несиметричний [3, с.126], то це приводить до несиметричності і довірчого інтервалу для випадкової величини, розподіленої за цим законом.
Для побудови довірчого інтервалу 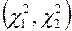 , в який з імовірністю
, в який з імовірністю 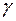 потрапить можливе значення
потрапить можливе значення 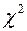 , виберемо його межі таким чином, щоб
, виберемо його межі таким чином, щоб
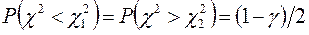 . (2.25)
. (2.25)
Для цього значення 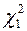 і
і 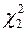 знайдемо за табл. 4 додатків, використовуючи рівняння
знайдемо за табл. 4 додатків, використовуючи рівняння
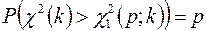 ,
, 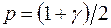 , (2.26)
, (2.26)
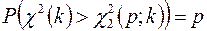 ,
, 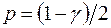 . (2.27)
. (2.27)
Із співвідношень (2.26), (2.27) з використанням протилежних подій і того, що для можливого значення 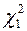
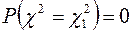 , випливає виконання рівностей (2.25).
, випливає виконання рівностей (2.25).
Отже, за побудовою подвійна нерівність
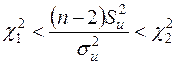 (2.28)
(2.28)
виконується з імовірністю 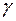 .
.
З першої нерівності (2.28) отримаємо рівносильну нерівність 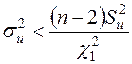 , а з другої:
, а з другої: 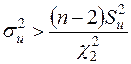 , об’єднання яких дає шуканий довірчий інтервал для оцінки
, об’єднання яких дає шуканий довірчий інтервал для оцінки 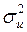 :
:
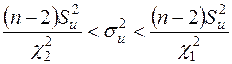 . (2.29)
. (2.29)
6. Вище були знайдені точкові МНК-оцінки невідомих параметрів регресії 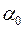 ,
, 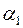 , а також їх числові характеристики. На перший погляд, наступний крок мав би полягати у побудові інтервальних оцінок для цих параметрів. Проте в полі зору необхідно тримати правомірність самої специфікації вихідної моделі (2.2), тобто теоретично можливі такі варіанти:
, а також їх числові характеристики. На перший погляд, наступний крок мав би полягати у побудові інтервальних оцінок для цих параметрів. Проте в полі зору необхідно тримати правомірність самої специфікації вихідної моделі (2.2), тобто теоретично можливі такі варіанти:
1) 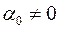 ,
, 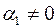 ; 2)
; 2) 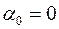 ,
, 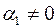 ; 3)
; 3) 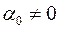 ,
, 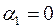 ; 4)
; 4) 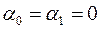 .
.
При цьому безпосередньо на підставі вибірки неможливо діагностувати кожний із цих варіантів, оскільки вибірка організовується випадковим чином. У той же час немає сенсу будувати довірчі інтервали для 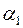 у випадках 3 та 4, а для
у випадках 3 та 4, а для 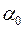 — у випадках 2 та 4.
— у випадках 2 та 4.
Відмітимо важливість діагностування рівності 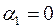 . У цьому випадку взагалі слід переглянути висунуту модель. Разом з тим, якщо
. У цьому випадку взагалі слід переглянути висунуту модель. Разом з тим, якщо 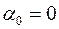 (при
(при 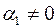 ), то це, як буде встановлено нижче, необхідно враховувати при розгляді питання про якість моделі.
), то це, як буде встановлено нижче, необхідно враховувати при розгляді питання про якість моделі.
Отже, актуальним є питання про з’ясування значущості коефіцієнтів регресії 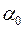 і
і 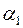 на підставі наявних статистичних даних.
на підставі наявних статистичних даних.
Висунемо статистичну нульову гіпотезу 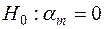 , де
, де 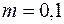 . Альтернативна гіпотеза
. Альтернативна гіпотеза 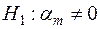 . Задамо також рівень значущості
. Задамо також рівень значущості 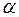 .
.
Згідно із (2.17) і (2.14) МНК-оцінки 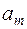 є незміщеними і лінійними відносно випадкових величин
є незміщеними і лінійними відносно випадкових величин 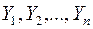 , які у відповідності із (2.8) розподілені нормально (
, які у відповідності із (2.8) розподілені нормально ( 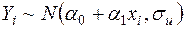 ,
, 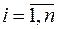 ). Тому і
). Тому і 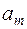 мають нормальний розподіл:
мають нормальний розподіл:
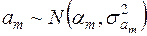 ,
, 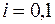 ,
,
де 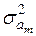 визначаються формулами (2.18), (2.19). Незміщеною оцінкою
визначаються формулами (2.18), (2.19). Незміщеною оцінкою 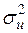 є
є 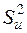 (формула (2.22)). Тому із врахуванням (2.18), (2.19) незміщені оцінки
(формула (2.22)). Тому із врахуванням (2.18), (2.19) незміщені оцінки 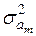 (вони невідомі, бо невідомим є
(вони невідомі, бо невідомим є 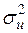 !) визначаються формулами
!) визначаються формулами
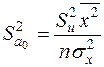 ,
, 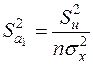 . (2.30)
. (2.30)
Розглянемо випадкову величину (1.13), де 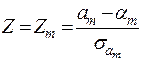 ,
, 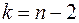 ,
, 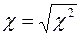 ,
, 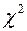 визначається за формулою (2.24), тобто
визначається за формулою (2.24), тобто
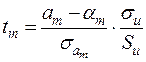 . (2.31)
. (2.31)
Вона має 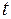 -розподіл із
-розподіл із 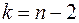 ступенями вільності і вже не залежить від
ступенями вільності і вже не залежить від 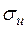 .
.
Враховуючи (2.18), (2.19) та (2.30), із (2.31) отримаємо такі 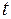 -розподіли:
-розподіли:
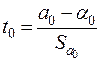 ,
, 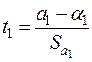 . (2.32)
. (2.32)
Зміст основної гіпотези 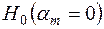 та альтернативної
та альтернативної 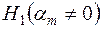 дозволяє сформулювати двосторонній критерій значущості оцінок
дозволяє сформулювати двосторонній критерій значущості оцінок 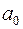 ,
, 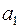 :
:
якщо виконується нерівність
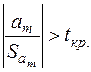 , (2.33)
, (2.33)
де 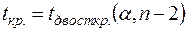 ,
, 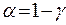 , — критична точка розподілу Ст’юден-та (табл. 3 додатків), тоді на рівні значущості
, — критична точка розподілу Ст’юден-та (табл. 3 додатків), тоді на рівні значущості 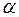 приймається гіпотеза
приймається гіпотеза 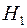 , тобто вважається, що
, тобто вважається, що 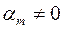 .
.
7. Нехай нерівність (2.33) виконується для 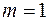 , що означає існування стохастичного зв’язку між змінними
, що означає існування стохастичного зв’язку між змінними 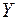 та
та 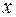 .
.
Побудуємо довірчий інтервал для функції регресії, тобто для умовного математичного сподівання 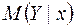 , який із заданою надійністю
, який із заданою надійністю 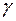 покриває невідоме значення
покриває невідоме значення 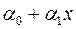 .
.
Знайдемо дисперсію групової середньої 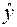 , яка є статистичною оцінкою
, яка є статистичною оцінкою 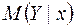 . Для цього рівняння регресії (2.11) запишемо у такому вигляді
. Для цього рівняння регресії (2.11) запишемо у такому вигляді
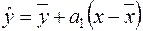 , (2.34)
, (2.34)
підставивши другу рівність (2.13) в (2.11). Перевагою рівняння (2.34) є некорельованість його доданків справа. Доведення рівності 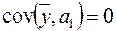 (за припущенням
(за припущенням 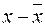 є детермінованою величиною) здійснюється з використанням (2.14), (2.4) і (2.16). Тому дисперсія лівої частини (2.34) дорівнює сумі дисперсій двох незалежних доданків правої:
є детермінованою величиною) здійснюється з використанням (2.14), (2.4) і (2.16). Тому дисперсія лівої частини (2.34) дорівнює сумі дисперсій двох незалежних доданків правої:
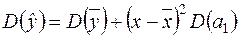 , (2.35)
, (2.35)
де 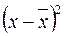 отримується внаслідок винесення детермінованого множника за знак дисперсії, піднесеного до квадрату.
отримується внаслідок винесення детермінованого множника за знак дисперсії, піднесеного до квадрату.
Згідно із (2.18) 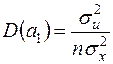 , а використання (2.8) дає
, а використання (2.8) дає
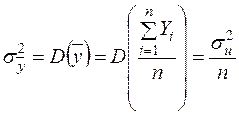 .
.
Отже, з (2.35)
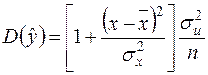 ,
,
а незміщена оцінка 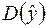 знаходиться за формулою:
знаходиться за формулою:
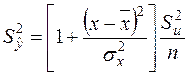 , (2.36)
, (2.36)
де 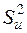 визначена формулою (2.22).
визначена формулою (2.22).
Розглянемо статистику (1.10)
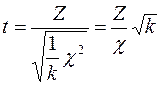 ,
,
поклавши 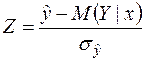 ,
, 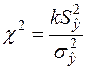 ,
, 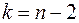 .
.
Використання передумов 1-4 та (1.7) дозволяє показати, що 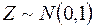 , а
, а 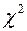 має розподіл
має розподіл 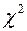 із
із 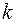 ступенями вільності, причому
ступенями вільності, причому 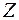 та
та 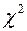 незалежні випадкові величини. Тому випадкова величина
незалежні випадкові величини. Тому випадкова величина
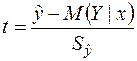
має 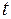 -розподіл Ст’юдента із
-розподіл Ст’юдента із 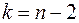 ступенями вільності. Оскільки густина
ступенями вільності. Оскільки густина 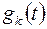 розподілу Ст’юдента парна, то
розподілу Ст’юдента парна, то
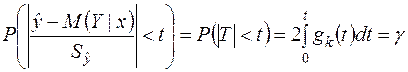 . (2.37)
. (2.37)
У табл. 2 додатків наведені значення 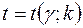 як кореня рівняння (2.37) в залежності від заданої довірчої імовірності
як кореня рівняння (2.37) в залежності від заданої довірчої імовірності 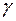 і від числа ступенів вільності
і від числа ступенів вільності 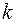 .
.
Таким чином, довірчий інтервал для невідомого умовного сподівання 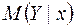 має такий вигляд:
має такий вигляд:
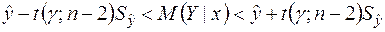 , (2.38)
, (2.38)
де 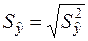 ,
, 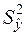 визначається формулою (2.36).
визначається формулою (2.36).
Якщо врахувати, що 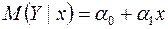 , а
, а 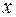 змінюється, то подвійна нерівність (2.38) дає довірчу зону для прямої регресії
змінюється, то подвійна нерівність (2.38) дає довірчу зону для прямої регресії 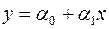 . Тому потрібно з’ясувати, яка поведінка «ширини» цієї зони при зміні
. Тому потрібно з’ясувати, яка поведінка «ширини» цієї зони при зміні 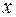 . Із формул (2.36) і (2.38) видно, що «ширина» зони мінімальна при
. Із формул (2.36) і (2.38) видно, що «ширина» зони мінімальна при 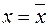 , а при віддаленні
, а при віддаленні 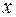 від
від 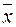 вона збільшується (мал. 2.1).
вона збільшується (мал. 2.1).
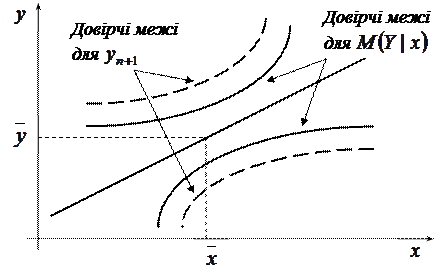
Малюнок 2.1.
Таким чином, прогноз значень залежної змінної 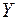 (в середньому) може призвести до значних похибок.
(в середньому) може призвести до значних похибок.
Побудова довірчої зони для функції регресії (або 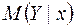 ) у випадку конкретної вибірки (іншими словами, довірчої зони для значень регресії в базисних точках) передбачає побудову точок з координатами
) у випадку конкретної вибірки (іншими словами, довірчої зони для значень регресії в базисних точках) передбачає побудову точок з координатами 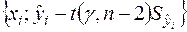 ,
, 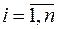 , з наступним з’єднанням сусідніх (по індексу
, з наступним з’єднанням сусідніх (по індексу 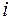 ) точок прямолінійними відрізками, а потім здійснення аналогічної процедури для послідовності точок
) точок прямолінійними відрізками, а потім здійснення аналогічної процедури для послідовності точок 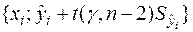 .
.
8. Нехай МНК-оцінки 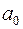 та
та 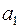 є значущими, тобто виконуються нерівності (2.33). Побудуємо довірчі інтервали для невідомих параметрів
є значущими, тобто виконуються нерівності (2.33). Побудуємо довірчі інтервали для невідомих параметрів 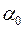 та
та 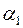 , використавши випадкові величини (2.32), які розподілені за законом Ст’юдента із
, використавши випадкові величини (2.32), які розподілені за законом Ст’юдента із 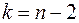 ступенями вільності.
ступенями вільності.
Позначимо 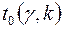 ,
, 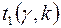 корені рівнянь
корені рівнянь
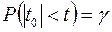 ,
, 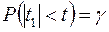
відповідно, які знаходяться за табл. 2 додатків. Тоді із надійністю 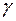 виконуються нерівності
виконуються нерівності
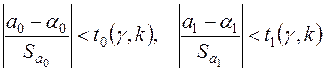 ,
,
звідки отримуються довірчі інтервали
 , (2.39)
, (2.39)
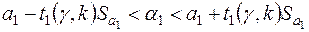 , (2.40)
, (2.40)
де 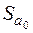 ,
, 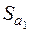 визначаються формулами (2.30).
визначаються формулами (2.30).
9. Основна мета дослідження моделі (2.2) — це статистично надійний точковий чи інтервальний прогноз значень залежної змінної 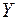 або її математичного сподівання. Для досягнення цієї мети необхідно з’ясувати якість моделі або значущість моделі, тобто встановити, чи відповідає модель експериментальним даним і чи достатньо включених в рівняння незалежних (пояснюючих) змінних (однієї або кількох) для описання залежної змінної. Перевірка значущості рівняння регресії проводиться на основі дисперсійного аналізу, який у даному випадку використовується як допоміжний засіб для вивчення якості регресійної моделі.
або її математичного сподівання. Для досягнення цієї мети необхідно з’ясувати якість моделі або значущість моделі, тобто встановити, чи відповідає модель експериментальним даним і чи достатньо включених в рівняння незалежних (пояснюючих) змінних (однієї або кількох) для описання залежної змінної. Перевірка значущості рівняння регресії проводиться на основі дисперсійного аналізу, який у даному випадку використовується як допоміжний засіб для вивчення якості регресійної моделі.
Розглянемо питання про декомпозицію дисперсій. Дисперсія спостережених значень залежної змінної має такий вигляд:
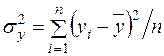 .
.
Відхилення 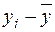 запишемо таким чином:
запишемо таким чином:
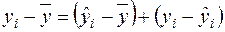 . (2.41)
. (2.41)
У статистиці різницю 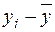 називають загальним відхиленням,
називають загальним відхиленням, 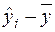 — відхиленням, яке можна пояснити моделлю,
— відхиленням, яке можна пояснити моделлю, 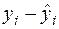 — непояснюваним відхиленням (яке не можна пояснити моделлю).
— непояснюваним відхиленням (яке не можна пояснити моделлю).
Піднесемо обидві частини (2.41) до квадрату та підсумуємо за індексом 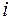 :
:
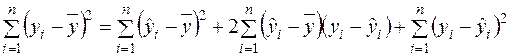 .
.
Якщо в моделі (2.2) 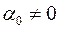 , тоді другий доданок в правій частині дорівнює нулю із врахуванням системи нормальних рівнянь (2.12):
, тоді другий доданок в правій частині дорівнює нулю із врахуванням системи нормальних рівнянь (2.12):
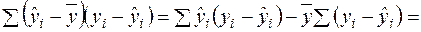
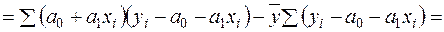
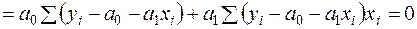 .
.
Тому остаточно отримаємо рівність
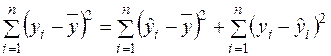 (2.42)
(2.42)
або
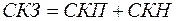 ,
,
де 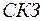 — загальна сума квадратів,
— загальна сума квадратів, 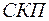 — пояснена сума квадратів,
— пояснена сума квадратів, 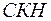 — непояснена сума квадратів.
— непояснена сума квадратів.
Поділивши (2.42) на 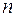 , отримаємо:
, отримаємо:
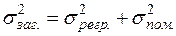 , (2.43)
, (2.43)
де 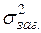 — загальна дисперсія,
— загальна дисперсія, 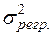 — дисперсія, що пояснює регресію,
— дисперсія, що пояснює регресію, 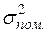 — дисперсія помилок.
— дисперсія помилок.
Для одержання незміщених оцінок дисперсій, які фігурують в рівності (2.43), потрібно знайти відповідні ступені вільності.
Для обчислення 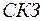 використовуються
використовуються 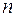 чисел
чисел 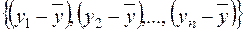 , серед яких лінійно незалежними є
, серед яких лінійно незалежними є 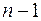 , оскільки
, оскільки 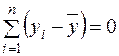 . Тому ступінь вільності
. Тому ступінь вільності 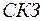 дорівнює
дорівнює 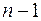 .
.
Із врахуванням (2.13) рівняння регресії можна записати у такому вигляді:
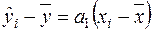 ,
,
звідки 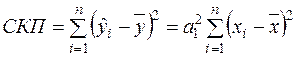 .
.
Отже, 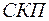 утворюється з використанням однієї одиниці незалежної інформації —
утворюється з використанням однієї одиниці незалежної інформації — 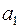 , тому ступінь вільності її дорівнює 1 або
, тому ступінь вільності її дорівнює 1 або 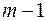 , де
, де 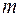 — число параметрів моделі (
— число параметрів моделі ( 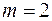 ).
).
Нарешті, 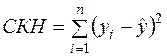 має (див. п.4)
має (див. п.4) 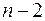 ступенів вільності.
ступенів вільності.
Означення. Число, яке отримується діленням суми квадратів на відповідний ступінь вільності, називається середнім квадратом.
Середні квадрати
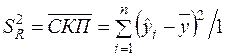 ,
, 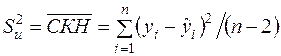 (2.44)
(2.44)
є незміщеними оцінками дисперсій залежної змінної, обумовлених відповідно регресією (пояснюючою змінною) і дією неврахованих факторів та помилок.
Повернемося до рівності (2.43). Якщо обидві її частини розділити на 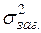 , то отримаємо
, то отримаємо
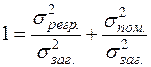 . (2.45)
. (2.45)
Означення. Перший доданок в правій частині (2.45) називається коефіцієнтом детермінації і позначається 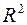 (або
(або 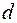 ):
):
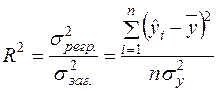 . (2.46)
. (2.46)
Із рівності (2.45) отримаємо рівносильну формулу для означення коефіцієнта детермінації:
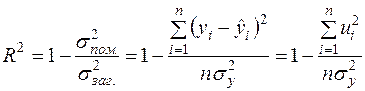 . (2.46*)
. (2.46*)
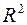 є однією із найбільш ефективних оцінок адекватності регресійної моделі, мірою її якості або характеристикою прогностичної сили моделі.
є однією із найбільш ефективних оцінок адекватності регресійної моделі, мірою її якості або характеристикою прогностичної сили моделі.
Величина 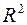 показує, яка частина (частка) варіації залежної змінної обумовлена варіацією пояснюючої змінної.
показує, яка частина (частка) варіації залежної змінної обумовлена варіацією пояснюючої змінної.
Оскільки доданки в рівності (2.45) невід’ємні, то з врахуванням (2.46) отримується подвійна нерівність 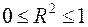 .
.
Чим ближче значення 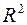 до одиниці, тим краще модель апроксимує емпіричні дані, тим ближче спостереження знаходяться по відношенню до прямої регресії. Якщо
до одиниці, тим краще модель апроксимує емпіричні дані, тим ближче спостереження знаходяться по відношенню до прямої регресії. Якщо 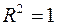 , то всі емпіричні точки
, то всі емпіричні точки 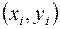 лежать на прямій регресії і між змінними
лежать на прямій регресії і між змінними 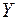 та
та 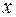 існує лінійна функціональна залежність. Якщо ж
існує лінійна функціональна залежність. Якщо ж 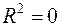 , то варіація залежної змінної повністю обумовлена дією неврахованих у моделі змінних і пряма регресії паралельна осі абсцис.
, то варіація залежної змінної повністю обумовлена дією неврахованих у моделі змінних і пряма регресії паралельна осі абсцис.
Дата добавления: 2016-06-13; просмотров: 643;
