Індивідуальне завдання №1 1 страница
Класична нормальна лінійна модель парної регресії.
Основні передумови нормальної класичної лінійної моделі парної регресії.
Знаходження оцінок параметрів.
Властивості МНК-оцінок.
Точкова оцінка дисперсії збурень. Число ступенів вільності.
Довірчий інтервал дисперсії збурень.
Перевірка значущості коефіцієнтів регресії.
Довірча зона функції регресії.
Довірчі інтервали коефіцієнтів регресії.
Критерії якості лінійної моделі. Коефіцієнт детермінації.
Прогнозування за класичною нормальною лінійною моделлю.
Задача.
1. Припустимо, що попереднім результатом специфікації моделі (1.3) є висновок про лінійну залежність між 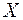 та
та 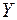 . Тоді модель (1.3) набере такого вигляду:
. Тоді модель (1.3) набере такого вигляду:
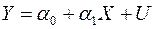 , (2.1)
, (2.1)
де 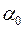 ,
,  — невідомі (теоретичні) детерміновані параметри,
— невідомі (теоретичні) детерміновані параметри, 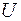 — невідома випадкова величина (збурення).
— невідома випадкова величина (збурення).
Приклади:
1) 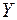 — річний обсяг заощаджень родини,
— річний обсяг заощаджень родини, 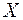 — річний дохід родини;
— річний дохід родини;
2) рівняння Кейнса: 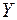 — індивідуальне споживання,
— індивідуальне споживання, 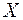 — наявний прибуток,
— наявний прибуток, 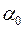 — величина автономного споживання,
— величина автономного споживання,  — гранична схильність до споживання (
— гранична схильність до споживання ( 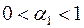 );
);
3) 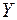 — річний товарообіг однієї філії торгівельного підприємства,
— річний товарообіг однієї філії торгівельного підприємства, 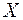 — торгівельна площа цієї філії;
— торгівельна площа цієї філії;
4) 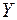 — валовий випуск продукції,
— валовий випуск продукції, 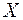 — вартість основних виробничих фондів підприємства.
— вартість основних виробничих фондів підприємства.
При моделюванні різних процесів розрізняють класичну і економетричну регресійні моделі.
У класичній лінійній моделі незалежна змінна вважається детермінованою величиною. В цьому параграфі будемо розглядати класичну лінійну модель
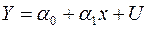 . (2.2)
. (2.2)
Зауваження. Передумова стосовно детермінованості незалежної змінної не виконується для багатьох прикладних регресійних моделей в економіці і соціології, в які часто включаються випадкові неконтрольовані величини (наприклад, ціни і кількість пропонованих товарів або товарів, що користуються попитом).
Нехай 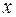 набирає значення
набирає значення 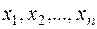 , де
, де 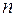 — обсяг вибірки. Ці статистичні дані можуть бути або просторовими, або часовими рядами, або ж перехресними рядами. Тоді із (2.2) отримується система
— обсяг вибірки. Ці статистичні дані можуть бути або просторовими, або часовими рядами, або ж перехресними рядами. Тоді із (2.2) отримується система 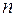 рівнянь
рівнянь
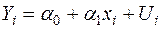 ,
, 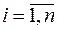 . (2.3)
. (2.3)
Повна специфікація моделі (2.2) передбачає виконання певних умов стосовно випадкової складової правої частини (2.3).
Передумова 1. Математичне сподівання збурень дорівнює нулю:
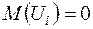 ,
, 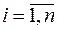 . (2.4)
. (2.4)
Ця передумова означає, що збурення в середньому не здійснюють на 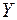 ніякого впливу. Справді, за властивостями математичного сподівання для
ніякого впливу. Справді, за властивостями математичного сподівання для 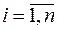 :
:
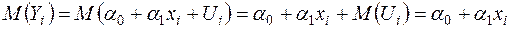 .
.
Передумова 2. Збурення мають однакову дисперсію:
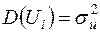 ,
, 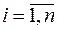 , (2.5)
, (2.5)
де 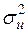 — невідоме число, яке підлягає оцінюванню.
— невідоме число, яке підлягає оцінюванню.
Якщо виконуються рівності (2.5), то говорять, що збурення гомоскедастичні, якщо ж ні — то збурення гетероскедастичні. Наведені терміни зумовлені тим, що функція 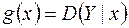 називається функцією скедастичності.
називається функцією скедастичності.
Передумова 3. Збурення 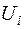 і
і 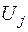 при
при 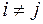 не корелюють між собою:
не корелюють між собою:
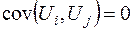
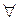
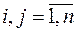 ,
, 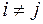 . (2.6)
. (2.6)
Враховуючи рівності (2.4) і формулу (1.18*), із (2.6) отримаємо рівності:
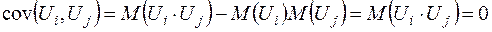 ,
,
тобто
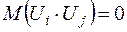 ,
, 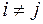 ,
, 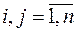 . (2.7)
. (2.7)
Передумова 4. Випадкові збурення 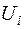 ,
, 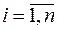 , розподілені за нормальним законом.
, розподілені за нормальним законом.
Згідно із передумовами 1, 2: 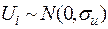 ,
, 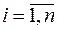 . Наслідком передумов 1-4 є нормальність розподілу випадкових величин
. Наслідком передумов 1-4 є нормальність розподілу випадкових величин 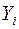 :
:
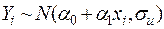 ,
, 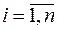 . (2.8)
. (2.8)
Зауваження. Передумови 1-4 стосовно моделі (2.3) разом визначають класичну нормальну лінійну модель регресії. Якщо ж передумова 4 не виконується, то має місце класична лінійна модель.
2. Перший крок на шляху дослідження моделі (2.2) полягає у параметризації цієї моделі, тобто, щоб за конкретною вибіркою 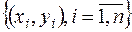 обсягом
обсягом 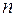 знайти такі значення оцінок невідомих параметрів
знайти такі значення оцінок невідомих параметрів 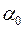 ,
,  , для яких побудована пряма регресії була б найкращою в певному сенсі серед усіх інших прямих.
, для яких побудована пряма регресії була б найкращою в певному сенсі серед усіх інших прямих.
Нехай 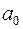 та
та 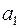 — оцінки невідомих параметрів
— оцінки невідомих параметрів 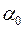 та
та  відповідно. Тоді оцінкою моделі (2.3) по вибірці є
відповідно. Тоді оцінкою моделі (2.3) по вибірці є 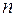 рівнянь
рівнянь
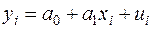 ,
, 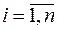 , (2.9)
, (2.9)
або
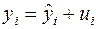 ,
, 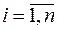 , (2.10)
, (2.10)
де  — групова середня, абоумовна середня, знайдена за рівнянням регресії
— групова середня, абоумовна середня, знайдена за рівнянням регресії
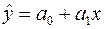 , (2.11)
, (2.11)
тобто 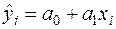 ,
,
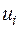 — вибіркова оцінка збурення
— вибіркова оцінка збурення 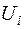 або залишок регресії, або ж відхилення.
або залишок регресії, або ж відхилення.
Згідно із (2.8)  можна назвати також розрахунковим або оціночним значенням
можна назвати також розрахунковим або оціночним значенням 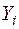 при
при 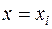 , оскільки
, оскільки 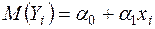 , а
, а 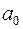 та
та 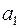 — оцінки
— оцінки 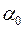 та
та  відповідно.
відповідно.
Мірою якості оцінок 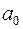 ,
, 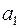 можуть бути визначені композиції відхилень
можуть бути визначені композиції відхилень 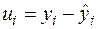 [7, с.28]. Найпоширенішим і теоретично обґрунтованим є метод, при якому мінімізується
[7, с.28]. Найпоширенішим і теоретично обґрунтованим є метод, при якому мінімізується 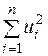 , і який має назву метод найменших квадратів (МНК). Перевагами його є оптимальні властивості оцінок (незміщеність, ефективність, спроможність), а також зручність з обчислювальної точки зору.
, і який має назву метод найменших квадратів (МНК). Перевагами його є оптимальні властивості оцінок (незміщеність, ефективність, спроможність), а також зручність з обчислювальної точки зору.
Використаємо МНК для знаходження 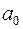 ,
, 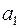 . Квадратична функція
. Квадратична функція
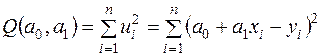
є неперервною, опуклою і обмеженою знизу ( 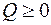 ), тому має мінімум. Необхідною умовою існування екстремуму неперервно диференційованої функції двох змінних є рівність нулю її частинних похідних:
), тому має мінімум. Необхідною умовою існування екстремуму неперервно диференційованої функції двох змінних є рівність нулю її частинних похідних:
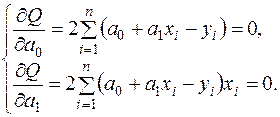
Цю систему рівнянь можна записати в такому вигляді:
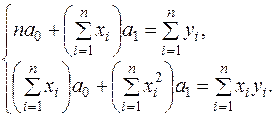
Поділимо кожне із рівнянь на 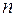 :
:
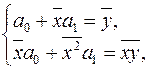 (2.12)
(2.12)
де 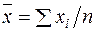 ,
, 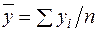 ,
, 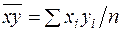 ,
, 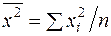 .
.
Використавши формулу Крамера, остаточно отримаємо єдиний розв’язок системи (2.12):
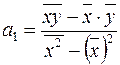 ,
, 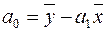 . (2.13)
. (2.13)
Отже, функція 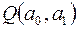 має єдину критичну точку. Виявляється [4, с.166], що в цій точці виконується і достатня умова існування мінімуму.
має єдину критичну точку. Виявляється [4, с.166], що в цій точці виконується і достатня умова існування мінімуму.
Оскільки оцінки (2.13) знайдені з допомогою МНК, то їх називають МНК-оцінками.
3. Для нефіксованої вибірки обсягом 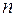 згідно із (2.3) результуюча ознака
згідно із (2.3) результуюча ознака 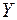 набирає значення
набирає значення 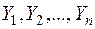 , які є випадковими величинами. Тоді за формулами (2.13)
, які є випадковими величинами. Тоді за формулами (2.13)
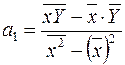 ,
, 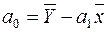 , (2.13*)
, (2.13*)
тобто ці оцінки є також випадковими величинами.
Необхідно з’ясувати якість цих статистичних оцінок.
Властивість 1. МНК-оцінки 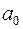 ,
, 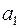 є лінійними комбінаціями спостережень
є лінійними комбінаціями спостережень 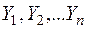 :
:
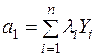 ,
, 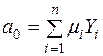 , (2.14)
, (2.14)
де
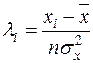 ,
, 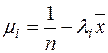 ,
, 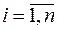 ,
, 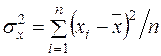 . (2.15)
. (2.15)
o Справді,
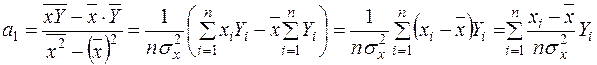 ,
,
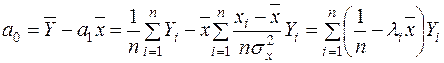 . ª
. ª
Зауваження. Вагові коефіцієнти 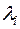 та
та 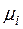 залишаються незмінними при переході від вибірки до вибірки. Вони задовольняють такі співвідношення:
залишаються незмінними при переході від вибірки до вибірки. Вони задовольняють такі співвідношення:
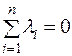 ,
, 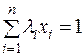 ,
, 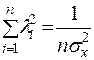 ,
, 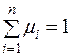 ,
, 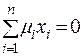 ,
, 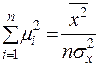 . (2.16)
. (2.16)
Пропонується самостійно перевірити правильність цих співвідношень.
Властивість 2. МНК-оцінки 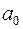 ,
, 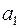 є незміщеними оцінками відповідних параметрів
є незміщеними оцінками відповідних параметрів 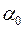 ,
,  .
.
o Використавши (2.8), (2.14), (2.16) і властивості математичного сподівання, отримаємо:
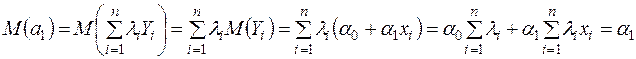 ,
,
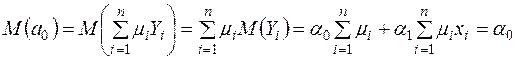 ,
,
тобто
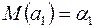 ,
, 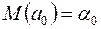 . ª (2.17)
. ª (2.17)
Властивість 3 (теорема Гаусса-Маркова). Із усіх лінійних незміщених оцінок параметрів 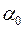 ,
,  тільки МНК-оцінки
тільки МНК-оцінки 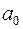 ,
, 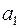 є ефективними і, отже, найкращими лінійними незміщеними оцінками.
є ефективними і, отже, найкращими лінійними незміщеними оцінками.
o Обчислимо спочатку 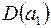 ,
, 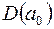 ,
, 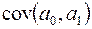 . Для цього встановимо некорельованість випадкових величин
. Для цього встановимо некорельованість випадкових величин 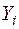 та
та 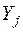 для
для 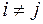 ,
, 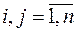 , використавши (2.3), (2.4) та (2.7) і детермінованість
, використавши (2.3), (2.4) та (2.7) і детермінованість 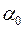 ,
,  та
та 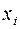 :
:
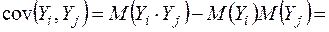
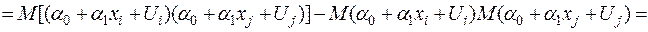
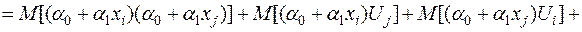
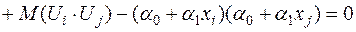 .
.
А тому із (2.14)-(2.16) та (2.8) отримаємо:
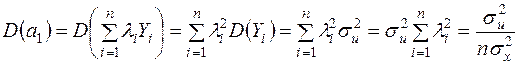 ; (2.18)
; (2.18)
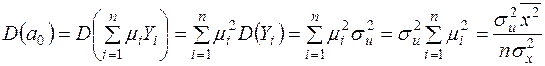 ; (2.19)
; (2.19)
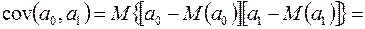
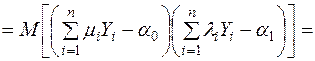
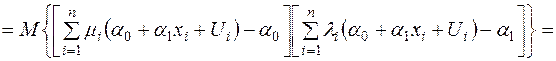
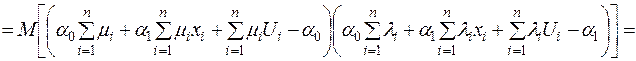
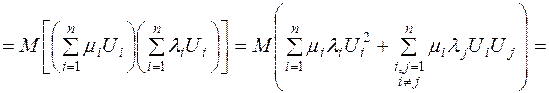
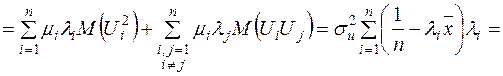
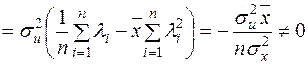 .
.
Отже, оцінки 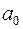 і
і 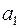 корелюють між собою, при цьому коваріаційна матриця цих оцінок має такий вигляд:
корелюють між собою, при цьому коваріаційна матриця цих оцінок має такий вигляд:

або більш компактно:
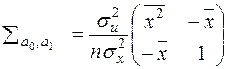 .
.
Зауваження. Символи 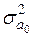 та
та 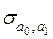 позначають
позначають 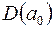 і
і 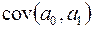 відповідно. Натомість символ
відповідно. Натомість символ 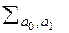 (велика літера «сигма» грецького алфавіту) позначає дисперсійно-коваріаційну матрицю (коротше: коваріаційну матрицю) двовимірної випадкової величини
(велика літера «сигма» грецького алфавіту) позначає дисперсійно-коваріаційну матрицю (коротше: коваріаційну матрицю) двовимірної випадкової величини 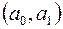 , втрачаючи значення символу суми.
, втрачаючи значення символу суми.
Розглянемо тепер довільні інші лінійні оцінки 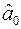 ,
, 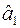 (відмінні від
(відмінні від 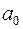 ,
, 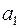 ) параметрів
) параметрів 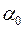 ,
,  такі, що
такі, що
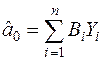 ,
, 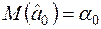 ,
, 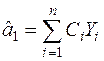 ,
, 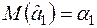 .
.
Згідно із формулюванням властивості 3, потрібно довести, що 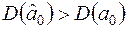 ,
, 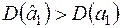 , тобто ефективність оцінок
, тобто ефективність оцінок 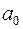 ,
, 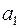 .
.
Доведемо, наприклад, другу нерівність. Нехай
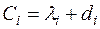 ,
, 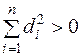 ,
,
де 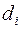 — зсув ваги
— зсув ваги 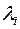 , визначеної (2.15), а друга нерівність зумовлена тим, що
, визначеної (2.15), а друга нерівність зумовлена тим, що 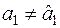 .
.
Із лінійності оцінки 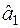 , рівнянь (2.3) та (2.4) отримуємо:
, рівнянь (2.3) та (2.4) отримуємо:
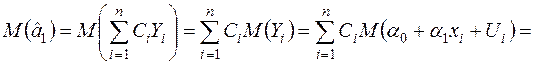
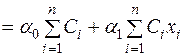 .
.
З другого боку, незміщеність 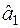 дає рівність
дає рівність 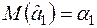 , тому повинні виконуватись рівності
, тому повинні виконуватись рівності
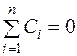 ,
, 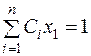 або
або 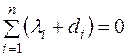 ,
, 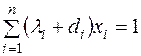 ,
,
звідки із врахуванням перших двох формул (2.16) отримуємо необхідні умови для зсувів 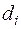 :
:
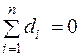 ,
, 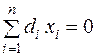 . (2.20)
. (2.20)
За аналогією з обчисленням 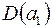 :
:
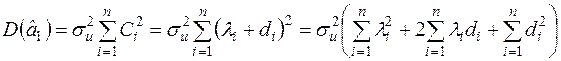 .
.
Але згідно із першою формулою (2.15) та (2.20):
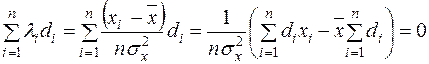 ,
,
а відповідно до (2.18):
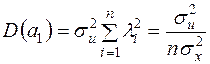 .
.
Тому остаточно:
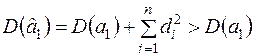 ,
,
що свідчить про ефективність оцінки 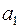 .
.
Аналогічно доводиться ефективність оцінки 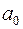 . ª
. ª
Властивість 4. МНК-оцінки є спроможними оцінками.
o Нагадаємо [4, с.51], що оцінка 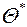 називається спроможною оцінкою параметра
називається спроможною оцінкою параметра 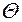 , якщо для як завгодно малого
, якщо для як завгодно малого 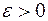 має місце граничний перехід
має місце граничний перехід
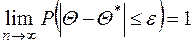 .
.
Згідно із нерівністю Чебишева: 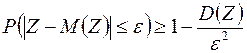 .
.
Для випадкової величини 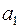 виконуються рівності
виконуються рівності 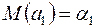 ,
, 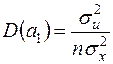 . Тому
. Тому 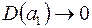 при
при 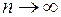 , тобто
, тобто 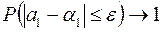 при
при 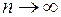 для як завгодно малого
для як завгодно малого 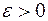 .
.
Аналогічно доводиться спроможність оцінки 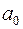 . ª
. ª
Висновки. При встановленні властивостей статистичних МНК-оцінок параметрів регресії в рамках класичної нормальної лінійної регресії були використані чотири умови стосовно випадкового збурення 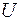 , які часто називаються умовами Гаусса-Маркова, а саме — передумови 1-3 і умова
, які часто називаються умовами Гаусса-Маркова, а саме — передумови 1-3 і умова 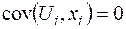
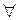
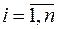 , яка виконується, оскільки за припущенням
, яка виконується, оскільки за припущенням 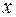 є детермінованою змінною.
є детермінованою змінною.
При невиконанні хоча б однієї з цих умов МНК-оцінки втрачають бажані властивості. Подолання складностей, які при цьому виникають, а також одержання більш надійних результатів — найважливіші задачі економетричного моделювання.
4. Вище були знайдені теоретичні числові характеристики МНК-оцінок. Для здійснення аналізу побудованої моделі (2.9), яка є оцінкою теоретичної моделі (2.3), потрібно знайти незміщені оцінки дисперсій (2.18), (2.19) для 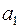 та
та 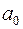 відповідно. Кожна з цих дисперсій містить невідомий співмножник
відповідно. Кожна з цих дисперсій містить невідомий співмножник 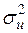 . Тому необхідно знайти незміщену точкову оцінку
. Тому необхідно знайти незміщену точкову оцінку 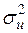 .
.
Вихідною інформацією для оцінювання 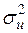 є значення
є значення 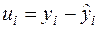 ,
, 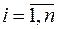 , тобто
, тобто 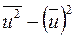 — можлива оцінка
— можлива оцінка 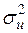 . Але
. Але
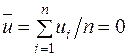 , (2.21)
, (2.21)
Дата добавления: 2016-06-13; просмотров: 731;
