Законы радиоактивного распада
Задача 2.1
Найти вероятность распада радиоактивного ядра за промежуток времени t, если известна его постоянная распада λ.
Решение
 Пусть в момент времени t = 0 ядро достоверно существует. Тогда к моменту времени t = t´ (рис. 2.1.1) имеется две возможности:
Пусть в момент времени t = 0 ядро достоверно существует. Тогда к моменту времени t = t´ (рис. 2.1.1) имеется две возможности:
1. Ядро не испытало радиоактивного распада и вероятность этого события q(t´);
2. Ядро распалось и вероятность этого события равна р(t´).
Очевидно, что
| q(t´) + р(t´) = 1, | (2.1.1) |
т.к. третьей возможности нет.
Рассмотрим, чему равна вероятность распада ядра за бесконечно малый промежуток времени dt´, не испытав при этом распада за время t´. Это событие сложное (см. рис. 2.1.1). Вероятность совместного появления обеих событий будет равна
| dр = q(t´)λdt´, | (2.1.2) |
где λdt´- вероятность распада за интервал времени dt´. Из (2.1.1) следует, что dp(t´) = - dq(t´). Произведя эту замену в (2.1.2), получаем дифференциальное уравнение для нахождения q(t´):
| dq= - q(t´)λdt´. | (2.1.3) |
Используя очевидное начальное условие q(t = 0) = 1 найдем, что вероятность ядру не распасться к заданному моменту времени
| q(t) = e-λt, | (2.1.4) |
а, в соответствии с (2.1.1), вероятность распада ядра за это же время составит
| p(t) = 1 - e-λt. | (2.1.5) |
Если в момент времени t = 0 имелось N0 радиоактивных ядер, то к моменту времени t наиболее вероятное (ожидаемое) число радиоактивных ядер, не испытавших радиоактивный распад, должно быть равным
| N(t) = N0q(t) = N0e-λt, |
что совпадает с (2.1). Реальное же число оставшихся ядер будет отличаться от N(t) в большую или меньшую сторону из-за случайного характера радиоактивного распада.
Задача 2.2
Показать, что среднее время жизни радиоактивных ядер τ = 1/λ, где λ – их постоянная распада.
Решение
По правилу нахождения среднего значения случайной величины
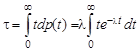 , ,
| (2.2.1) |
поскольку dp(t) – вероятность (вероятность р(t) нормирована на единицу!) того, что ядро, прожив время t, распадется между t и t + dt, а вероятность p(t) получена в предыдущей задаче (см. (2.1.4)). Выполняя в (2.2.1) интегрирование по частям, получим
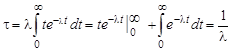 . .
|
Задача 2.3
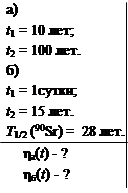 Какая доля первоначального количества ядер 90Sr: а) останется через 10 и 100 лет; б) распадется за одни сутки; за 15 лет?
Какая доля первоначального количества ядер 90Sr: а) останется через 10 и 100 лет; б) распадется за одни сутки; за 15 лет?
Решение
Будем предполагать, что первоначальное количество ядер настолько велико, что доли распавшихся ηа и доли оставшихся ηб ядер совпадают с вероятностями q(t) (2.1.4) и p(t) (2.1.5) соответственно, полученными в задаче 2.1. Необходимую величину постоянной распада λ = ln2/Т1/2 определим через период полураспада, величину которого найдем в таблице табл. 1 Приложений.
а)
ηа(t) = e-λt = 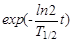 .
.
ηа(t1) = 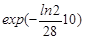 = 0,78.
= 0,78.
ηа(t2) = 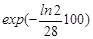 = 0,084.
= 0,084.
б)
ηб(t) = 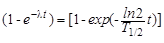 .
.
ηб(t1) = 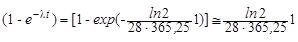 = 6,8·10-5
= 6,8·10-5
ηб(t1) = 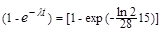 =0,31
=0,31
Задача 2.4
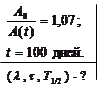 Вычислить постоянную распада, среднее время жизни и период полураспада радиоактивного нуклида, активность A(t) которого уменьшается в 1,07 раза за 100 дней.
Вычислить постоянную распада, среднее время жизни и период полураспада радиоактивного нуклида, активность A(t) которого уменьшается в 1,07 раза за 100 дней.
Решение
Активность по определению – среднее число распадающихся ядер в единицу времени (см. формулу (2.2)).
Число ядер, которые должны испытать распад за время t,
| Nd(t) = N0 – N(t) = N0(1 - e-λt). | (2.4.1) |
Дифференцируя (2.4.1) по времени, получим формулу (2.2):
| А(t) = λ N0 e-λt = А0 e-λt, | (2.4.2) |
где А0 = λN0 – активность в начальный момент времени. Таким образом,
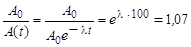 .
.
Решая последнее уравнение относительно λ, получим
 .
.
Найти τ и Т1/2 рекомендуется самостоятельно, используя приведенные выше формулы.
Задача 2.5
Определить возраст древних деревянных предметов, у которых удельная активность 14С составляет 3/5 удельной активности этого же нуклида в только что срубленных деревьях.
Решение
Радиоактивный углерод 14С, период полураспада которого Т1/2 = 5730 лет, непрерывно образуется в верхних слоях атмосферы Земли из азота 14N под действием космического излучения. Благодаря ветрам и океанским течениям равновесная концентрация 14С в различных местах земного шара одинакова и равна примерно 15 распадам в минуту на каждый грамм углерода в составе живых организмов. Пока организм жив в результате процессов обмена концентрация 14С в нем остается постоянной из-за круговорота веществ в природе. После смерти организма усвоение 14С прекращается и его количество начинает убывать по обычному закону (2.1) радиоактивного распада, что позволяет определить дату смерти или, как говорят археологи, возраст.
Согласно (2.2) и условию задачи
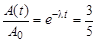 ,
,
откуда
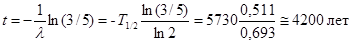
Задача 2.6
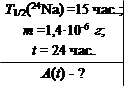 Свежеприготовленный препарат содержит 1,4 мкг радиоактивного нуклида 24Nа. Какую активность он буде иметь через сутки?
Свежеприготовленный препарат содержит 1,4 мкг радиоактивного нуклида 24Nа. Какую активность он буде иметь через сутки?
Решение
Согласно (2.2)

Задача 2.7
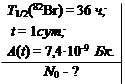 Определить число радиоактивных ядер в свежеприготовленном препарате 82Br, если известно, через сутки его активность стала равной 7,4·10-9 Бк (0,4 Ки).
Определить число радиоактивных ядер в свежеприготовленном препарате 82Br, если известно, через сутки его активность стала равной 7,4·10-9 Бк (0,4 Ки).
Решение
Из формулы (2. 2) следует, что

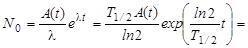
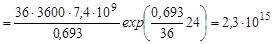
Задача 2.8
Вычислить удельную активность чистого 239Pu.
Решение
Удельная активность нуклида – активность единицы массы этого нуклида:
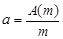 . .
| (2.8.1) |
Для нуклида (без учета вторичных компонент, возникающих после распада)
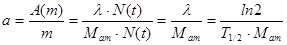 , ,
| (2.8.2) |
т.е. удельная активность нуклида не зависит от времени. Учитывая, что T1/2(239Pu) = 24000 лет, получим
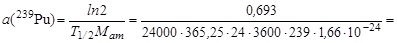
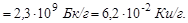
Задача 2.9
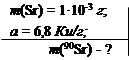 Сколько миллиграмм β-активного 90Sr следует добавить к 1 мг неактивного стронция, чтобы удельная активность препарата стала равной 6,8 Ки/г?
Сколько миллиграмм β-активного 90Sr следует добавить к 1 мг неактивного стронция, чтобы удельная активность препарата стала равной 6,8 Ки/г?
Решение
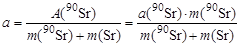 . .
| (2.9.1) |
Из этого уравнения
 .
.
Удельную активность нуклида 90Sr, период полураспада которого Т1/2 = 28 лет, вычислим по формуле (2.8.2):
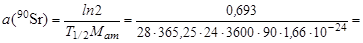
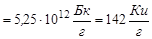 .
.
Используем полученную удельную активность нуклида 90Sr для получения ответа:
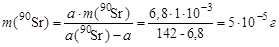 .
.
Задача 2.10
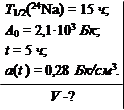 В кровь человека ввели небольшое количество раствора, содержащего 24Nа активностью А0 = 2,1·103 Бк. Активность одного см-3 крови, взятой через t = 5 ч после этого, оказалась равной а = 0,28 Бк/см3. Найти объем крови человека.
В кровь человека ввели небольшое количество раствора, содержащего 24Nа активностью А0 = 2,1·103 Бк. Активность одного см-3 крови, взятой через t = 5 ч после этого, оказалась равной а = 0,28 Бк/см3. Найти объем крови человека.
Решение
Будем предполагать, что за 5 часов концентрация атомов 24Nа в крови человека стала одинаковой. Тогда
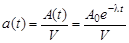 .
.
Из этого уравнения находим
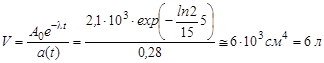 .
.
Задача 2.11
При радиоактивном распаде ядер нуклида А1 образуется радионуклид А2. Их постоянные распада равны λ1 и λ2. Полагая, что в начальный момент препарат содержал только ядра нуклида А1 в количестве N01, определить:
а) количество ядер нуклида А2 через промежуток времени t;
б) промежуток времени, через который количество ядер нуклида А2 достигнет максимума;
в) в каком случае может возникнуть состояние переходного равновесия, когда относительное количество обоих нуклидов будет оставаться постоянным. Чему равно это отношение?
Решение
а) Распад первого нуклида описывается обычным уравнением (2.1) для радиоактивного распада:
| N1(t) = N10 exp(-λ1t), | (2.11.1) |
где N10 - начальное количество ядер нуклида А1.
Распад второго нуклида описывается дифференциальным уравнением, которое устанавливает баланс среднего числа ядер нуклида А2 за время dt:
| dN2 = λ1N1dt – λ2N2dt. | (2.11.2) |
Первый член в правой части (2.11.2) дает среднее число ядер нуклида А2, которые возникают за время dt, второй - среднее число ядер нуклида А2, которые распадаются за время dt. С учетом (2.11.1) уравнение (2.11.2) приобретает вид:
| dN2/d t = λ1N10exp(-λ1t)– λ2N2. | (2.11.3) |
Уравнение (2.11.3) будем решать методом вариации постоянной.
Решение однородного уравнения, получаемого из (2.11.3), есть
| N2 (t) = С(t) exp(-λ2t), | (2.11.4) |
в котором С(t) – некоторая функция, которую нужно найти. Подставив в (2.11.3) функцию (2.11.4) и ее производную, получим дифференциальное уравнение для нахождения функции С(t):
dС/d t = λ1N10exp[(λ2 - λ) t],
решение которого есть
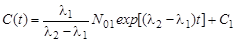 . .
| (2.11.5) |
Константа С1 определяется из начальных условий.
Подставив (2.11.5) в (2.11.4), получим
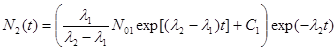 . .
| (2.11.5) |
Если при t = 0, N20 = 0, то окончательно имеем
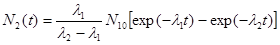 . .
| (2.11.6) |
б) Дифференцируя (2.11.6) по времени и приравняв к нулю производную, получим уравнение для нахождения tm – времени накопления максимального числа ядер нуклида А2:
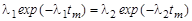 ,
,
из которого
 . .
| (2.11.7) |
в) Учитывая (2.11.1), получим из (2.11.6) следующее отношение
 .
.
Если λ2 >> λ1 [(T1/2)2 << (T1/2)2] и t >> 1/ λ2 ≈ (T1/2)2, то
 . .
| (2.11.8) |
Таким образом, получена формула (2.4).
Задача 2.12
Нуклид 226Ra, являясь продуктом распада 238U, содержится в последнем в количестве одного атома на каждые 2,80·106 атомов 238U. Найти период полураспада 238U, если известно, что он значительно больше периода полураспада 226Ra, который равен 1620 годам.
Решение
Для решения используем формулу (2.11.8) из предыдущей задачи, так как условия, при которых она справедлива, соблюдены:
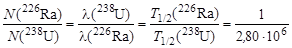 ,
,
откуда
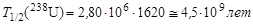 .
.
Задача 2.13
При β-распаде 112Pd возникает β-активный нуклид 112Ag. Их периоды полураспада равны соответственно 21 и 3,2 ч. Найти отношение максимальной активности нуклида 112Ag к первоначальной активности препарата, если в начальный момент препарат содержал только нуклид 112Pd.
Решение
Будем обозначать индексом «1» величины, относящиеся к 112Pd, а индексом «2» величины, относящиеся к 112Ag. Тогда

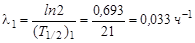 ;
; 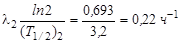 .
.
Искомое отношение
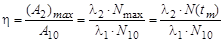 , ,
| (2.13.1) |
где N(tm) – максимальное число атомов нуклида 112Ag, которое накапливается за время tm (2.11.7). Используя (2.11.6), получим
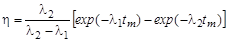 . .
| (2.13.2) |
Вычислим, используя (2.11.7),

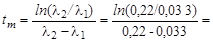
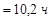 ,
,
а затем по формуле (2.13.2) вычислим

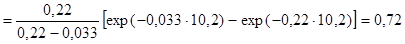 .
.
Задача 2.14
Радионуклид испытывает превращение по цепочке:
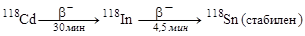
(под стрелками указаны соответствующие периоды полураспада). Считая, что в начальный момент t = 0 препарат содержал только 118Cd, найти:
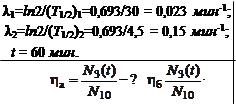 а) какая часть ядер превратиться в стабильные ядра через 60 мин;
а) какая часть ядер превратиться в стабильные ядра через 60 мин;
б) во сколько раз уменьшится активность препарата через 60 мин.
Решение
а) Пусть N10 – первоначальное количество ядер, а N3(t) - количество образовавшихся ядер 118Sn за время t.
В свою очередь, количество образовавшихся ядер 118Sn за время t равно числу распавшихся ядер 118In за этот же промежуток времени:
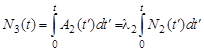 ,
,
где N2(t) и λ2 – зависимость числа ядер 118In от времени и их постоянная распада. Используя формулу (2.11.6), получим
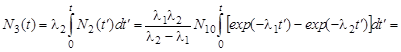

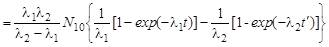 .
.
Таким образом,
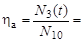
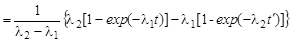 .
.
Величину ηа вычислить самостоятельно (ηа = 0,7).
б) Активность препарата через время t составит
A(t) = A1(t) + A2(t) = λ1·N1(t) + λ2·N2(t).
Тогда
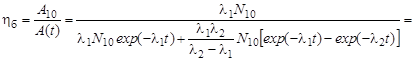
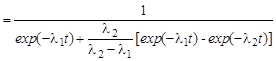 .
.
Величину ηб вычислить самостоятельно (ηб = 1,85).
Задача 2.15
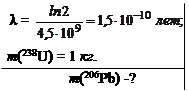 Определить массу свинца, который образуется из 1,0 кг 238U за период, равный возрасту горных пород (2,5·109 лет).
Определить массу свинца, который образуется из 1,0 кг 238U за период, равный возрасту горных пород (2,5·109 лет).
Решение
206Pb является конечным и стабильным элементом в радиоактивном семействе (ряду) урана, родоначальником которого является 238U. Поскольку суммарный период полураспада всех последующих звеньев семейства много меньше, чем период полураспада 238U, то с хорошей точностью можно считать, что период полураспада, приводящий к образованию 206Pb, равен в точности периоду полураспада 238U.
Искомая масса 206Pb будет равна
| m(206Pb) = Мат(206Pb)·N(206Pb) = Мат(206Pb)· Np(238U), | (2.15.1) |
где Np(238U) – количество распавшихся ядер 238U за время t, которые, в конечном итоге, превратились в равное количество ядер 206Pb. Если первоначальное количество ядер 238U равнялось
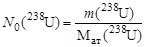 ,
,
то количество распавшихся ядер 238U за время t составит
 .
.
Подставив последнее выражение в (2.15.1), получим
m(206Pb) = 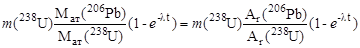 =
=
 = 0,27 кг.
= 0,27 кг.
Задача 2.16
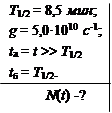 Радионуклид 27Mg образуется с постоянной скоростью g = 5,0·1010 ядер в секунду. Определить количество ядер 27Mg, которое накопится в препарате через промежуток времени: а) значительно превышающий его период полураспада; б) равный периоду полураспада.
Радионуклид 27Mg образуется с постоянной скоростью g = 5,0·1010 ядер в секунду. Определить количество ядер 27Mg, которое накопится в препарате через промежуток времени: а) значительно превышающий его период полураспада; б) равный периоду полураспада.
Решение
Рассмотрим изменение dN ядер 27Mg в течение малого промежутка времени dt:
| dN = gdt – λNdt, | (2.16.1) |
где gdt - количество рождаемых ядер, а λNdt - количество распадающихся ядер за время dt.Интегрируя это уравнение с начальным условием N(t = 0) = 0, получим формулу (2.3):
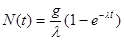 . .
|
а) Предельный переход в (2.3) при t → ∞ дает
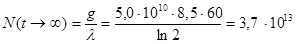 .
.
Полученный результат определяет максимально возможное количество ядер 27Mg, которое может образоваться при заданных условиях.
б) Если t = T1/2 , то выражение в скобках в (2.3) равно 1/2 и с учетом результата п. а), получим
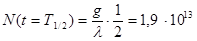 .
.
Задача 2.17
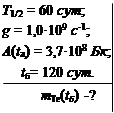 Радионуклид 124Sb образуется с постоянной скоростью g = 1,0·109 ядер в секунду. С периодом полураспада Т1/2 = 60 сут он превращается в стабильный нуклид 124Те. Найти:
Радионуклид 124Sb образуется с постоянной скоростью g = 1,0·109 ядер в секунду. С периодом полураспада Т1/2 = 60 сут он превращается в стабильный нуклид 124Те. Найти:
а) через сколько времени после начала образования активность 124Sb станет А = 3,7·108 Бк.
б) какая масса нуклида 124Те накопится в препарате за четыре месяца после начала его образования.
Решение
а) Умножая правую и левую части формулы (2.3) на постоянную распада λ нуклида 124Sb, получим уравнение
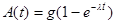 , ,
| (2.17.1) |
из которого
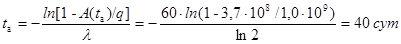 .
.
б) Так как распад каждого атома нуклида 124Sb сопровождается образованием атома стабильного нуклида 124Те, то его масса за время t после начала образования нуклида 124Sb будет равна:
mTe(t) = Мат(124Те)·N(t),
где N(t) – количество ядер нуклида 124Sb, распавшихся за время t. В свою очередь
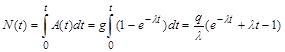 ,
,
если для вычисления A(t) использовать (2.17.1).
Окончательно получим
mTe(tб) = Мат(124Те)· 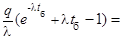
= 124·1,66·10-24  [exp
[exp 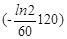 +
+ 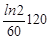 -1]
-1] 
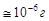 .
.
Задача 2.18
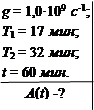 Радионуклид 138Xe, который образуется с постоянной скоростью g= 1,0·109 ядер в секунду, испытывает превращение по схеме
Радионуклид 138Xe, который образуется с постоянной скоростью g= 1,0·109 ядер в секунду, испытывает превращение по схеме
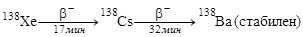
(под стрелками указаны периоды полураспада). Вычислить суммарную активность препарата через 60 мин после начала накопления.
Решение
Искомая активность
| А(t) = А1(t) + А2(t) = А1(t) + λN2(t). | (2.18.1) |
Зависимость А1(t) активности нуклида 138Xe выражается формулой (2.17.1). Для нахождения зависимости N2(t) накопления ядер нуклида 138Сs необходимо решить уравнение
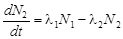 ,
,
где N1(t) и N2(t) выражают накопление ядер 138Xe и 138Сs, а N1(t) вычисляется по формуле (2.3). Тогда
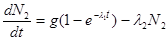
Решение этого уравнения, которое получается методом вариации постоянной (см. задачу 2.11), при N2(t=0) = 0 имеет вид:
 .
.
Подставив полученное решение и (2.17.1) в (2.18.1), получим окончательно
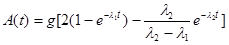 .
.
Вычисление величины А проделать самостоятельно (А = 1,4·1010 Бк).
α- и β-распады, γ-излучение ядер
Задача 2.19
 Покоящиеся ядро 213Ро испустило α-частицу с кинетической энергией Тα = 8,34 МэВ. При этом дочернее ядро оказалось непосредственно в основном состоянии. Найти полную энергию Qα, освобождаемую в этом процессе. Какую долю этой энергии составляет кинетическая энергия дочернего ядра? Какова скорость отдачи дочернего ядра.
Покоящиеся ядро 213Ро испустило α-частицу с кинетической энергией Тα = 8,34 МэВ. При этом дочернее ядро оказалось непосредственно в основном состоянии. Найти полную энергию Qα, освобождаемую в этом процессе. Какую долю этой энергии составляет кинетическая энергия дочернего ядра? Какова скорость отдачи дочернего ядра.
Решение
1). Запишем схему α-распада ядра 213Ро:
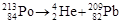 .
.
Так как освобождаемая энергия Еα переходит в кинетическую энергию продуктов распада, то при распаде покоящегося ядра 213Ро:
| Qα = Тα + Тя. | (2.19.1) |
Закон сохранения импульса:
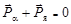 ,
,
или
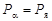 , ,
| (2.19.2) |
поскольку исходное ядро покоится. Т.к. Тα << Мα а, следовательно, и Тя << Мя, то можно использовать классическую связь между кинетической энергией и импульсом:
 .
.
В этом случае с помощью (2.19.2) получаем, что
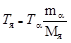 . .
| (2.19.3) |
Подставив (2.19.3) в (2.19.1) и решая полученное уравнение относительно Еα, получим
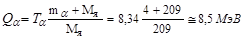 . .
| (2.19.4) |
2). Доля кинетической энергии Тя ядра 209Pb от полной энергии Qα, высвобождаемой при α-распаде ядра 213Ро, составит

3). Скорость ядра отдачи
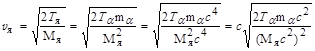 =
=
 = 3,8·105 м/с.
= 3,8·105 м/с.
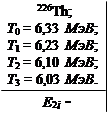 Задача 2.20
Задача 2.20
Распад 226Th ядер происходит из основного состояния и сопровождается испусканием α-частиц с кинетическими энергиями 6,33; 6,23; 6,10 и 6,03 МэВ. Рассчитать и построить схему уровней дочернего ядра.
Решение
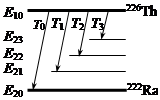 Построим энергетическую диаграмму α-переходов ядра 226Th. Жирными линиями обозначены основные уровни энергии материнского и дочернего ядра. Суммарная кинетическая энергия ядра отдачи 222Ra и α-частицы при рождении дочернего ядра в одном из возможных энергетических состояний равна, согласно (2.19.4),
Построим энергетическую диаграмму α-переходов ядра 226Th. Жирными линиями обозначены основные уровни энергии материнского и дочернего ядра. Суммарная кинетическая энергия ядра отдачи 222Ra и α-частицы при рождении дочернего ядра в одном из возможных энергетических состояний равна, согласно (2.19.4),
 . .
| (2.20.1) |
Тогда, если энергию E20 основного уровня дочернего принять за ноль, энергии уровней будут иметь следующие значения:
 .
.
Задача 2.21
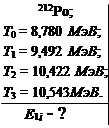 При распаде ядер 212Ро испускаются четыре группы α-частиц: основная с кинетической энергией 8,780 МэВ и длиннопробежные с кинетическими энергиями 9,492; 10,422 и 10,543 МэВ. Рассчитать и построить схему уровней ядра 212Ро, если известно, что дочерние ядра во всех случаях возникают непосредственно в основном состоянии.
При распаде ядер 212Ро испускаются четыре группы α-частиц: основная с кинетической энергией 8,780 МэВ и длиннопробежные с кинетическими энергиями 9,492; 10,422 и 10,543 МэВ. Рассчитать и построить схему уровней ядра 212Ро, если известно, что дочерние ядра во всех случаях возникают непосредственно в основном состоянии.
Решение
Ядра 212Ро, имеющие период полураспада относительно α-распада около 2·10-7 с, рождаются в результате β-распада ядер 212At, причем преимущественно в одном из возбужденных состояний. У ядер с существенно большими периодами полураспада по отношению к α-распаду, сначала имеет место переход в основное состояние с испусканием γ-квантов, после чего α-распад. Однако из-за очень малого времени жизни по отношению к α-распаду небольшая, но заметная часть возбужденных ядер 212Ро будет испытывать α-распад из возбужденных состояний. При этом к энергии α-распада 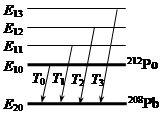 добавляется энергия возбуждения материнского ядра и возникающие таким образом α-частицы имеют бóльшую энергию, чем испущенные из основного состояния. Возникающая ситуация иллюстрируется с помощью диаграммы возможных энергетических переходов при α-распаде ядер 212Ро. Тогда, согласно формулам (2.19.1) и (2.20.1), возможные уровни энергий ядра 212Ро будут иметь следующие значения:
добавляется энергия возбуждения материнского ядра и возникающие таким образом α-частицы имеют бóльшую энергию, чем испущенные из основного состояния. Возникающая ситуация иллюстрируется с помощью диаграммы возможных энергетических переходов при α-распаде ядер 212Ро. Тогда, согласно формулам (2.19.1) и (2.20.1), возможные уровни энергий ядра 212Ро будут иметь следующие значения:
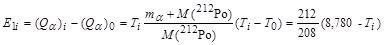 .
.
Задача 2.22
Оценить высоту кулоновского барьера для α-частиц, испускаемых ядрами 222Rn (закруглением вершины барьера пренебречь). Какова у этих ядер ширина барьера (туннельное расстояние) для α-частиц, вылетающих с кинетической энергией 5,5 МэВ.
Решение
Если пренебречь линейными размерами α-частицы и считать ее точечным объектом, то кулоновский барьер будет иметь остроконечную форму. Из формулы (2.15)
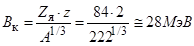 .
.
Очевидно, что полученная оценка несколько завышена.
Если предположить, что кинетическая энергия α-частицы по обе стороны потенциального барьера Тк = Тα = 5,5 МэВ, то ширина барьера (туннельное расстояния) – область, классически недоступная α-частице, представлена на схеме отрезком RяR1.
Для нахождения радиуса ядра 222Rn воспользуемся формулой (1.1):
Rя = 1,4·10-13A1/3 = 1,4·10-132221/3 = 8,5·10-13 см.
 Положение точки R1 на оси r найдем из условия равенства потенциальной энергии α-частицы в электрическом поле ядра 222Rn в точке R1 и ее кинетической энергии Тк:
Положение точки R1 на оси r найдем из условия равенства потенциальной энергии α-частицы в электрическом поле ядра 222Rn в точке R1 и ее кинетической энергии Тк:
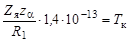 ,
,
если использовать формулу (2.14). Из последнего уравнения

Ширина барьера составит
R1 – Rя = (42,8 – 8,5)·10-13 = 3,4·10-12 см.
Задача 2.23
Определить отношение высоты центробежного барьера к высоте кулоновского барьера для α-частиц, испускаемых ядрами 209Ро, с орбитальным моментом l = 2. Закруглением вершины кулоновского барьера пренебречь.
Решение.
α-Частица может покидать ядро не только двигаясь точно по лини, проходящей через центр инерции системы дочернее ядро – α-частица, т.е. с l = 0, но и покидать ядро, имея орбитальный момент l > 0. В этом случае, кинетическая энергия α-частицы, необходимая для преодоления кулоновского барьера, уменьшается на величину центробежной энергии на границе ядра:
Тк = Тα – Bц.
Таким образом, возникает центробежный барьер, который необходимо преодолеть α-частице как при входе в ядро, так и покидая его. В классической механике центробежная энергия двух тел массой M и m, вращающихся вокруг центра инерции c линейными скоростями V и v соответственно, равна
 ,
,
 т.к. вращение обоих тел относительно центра инерции (точка «о») происходит с одинаковой угловой скоростью и поэтому V/v = r/R = m/M (см. схему). Продолжая преобразования, получим
т.к. вращение обоих тел относительно центра инерции (точка «о») происходит с одинаковой угловой скоростью и поэтому V/v = r/R = m/M (см. схему). Продолжая преобразования, получим

 .
.
Учитывая, что механический (орбитальный) момент  α-частицы может принимать только дискретные значения,
α-частицы может принимать только дискретные значения,
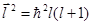 ,
,
величины которых определяются орбитальным квантовым числом l = 0,1,2,…, получим выражение для центробежного потенциала:

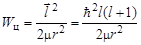 ,
,
где 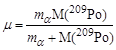 - приведенная масса α-частицы и ядра 209Ро. Значение Wц при r = Rя называется высотой центробежного барьера
- приведенная масса α-частицы и ядра 209Ро. Значение Wц при r = Rя называется высотой центробежного барьера
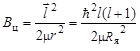 . .
| (2.23.1) |
Последовательное квантовомеханическое рассмотрение приводит к такому же выражению для центробежного барьера.
Используя формулу (2.15) для высоты кулоновского барьера, получим окончательно
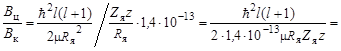
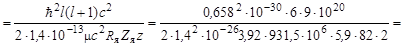
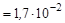
Задача 2.24
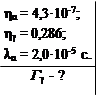 Найти ширину первого возбужденного уровня ядер 214Ро по отношению к испусканию γ-квантов, если известно, что при распаде с этого уровня на каждую α-частицу основной группы испускается в среднем 4,3·10-7 длиннопробежных α-частиц и 0,286 γ-квантов. Постоянная распада по отношению к испусканию длиннопробежных α-частиц равна 2,0·105 с.
Найти ширину первого возбужденного уровня ядер 214Ро по отношению к испусканию γ-квантов, если известно, что при распаде с этого уровня на каждую α-частицу основной группы испускается в среднем 4,3·10-7 длиннопробежных α-частиц и 0,286 γ-квантов. Постоянная распада по отношению к испусканию длиннопробежных α-частиц равна 2,0·105 с.
Решение
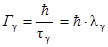
| (2.24.1) |
Число длиннопробежных α-частиц на одну основную
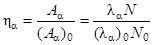 . .
| (2.24.2) |
То же для γ-квантов:
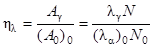 . .
| (2.24.3) |
В (2.24.2) и (2.24.3): (Аα)0и Аα– активности α-распада из основного и возбужденного состояний; Аγ – активность по отношению к испусканию γ-квантов из возбужденного состояния; N0 и N - количество ядер 214Ро в основном и возбужденном состояниях; (λα)0, λα и λγ – соответствующие постоянные распада.
Отношение (2.24.3) к (2.24.2) дает
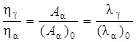 , ,
| (2.24.4) |
откуда
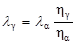 . .
| (2.24.5) |
Подставив (2.24.5) в (2.24.1), получим

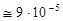 эВ. эВ.
| (2.24.6) |
Задача 2.25
Вычислить суммарную кинетическую энергию частиц, возникающих при β-распаде покоящегося нейтрона.
Решение
Распад свободного (изолированного от действия ядерных сил) нейтрона происходит по схеме:
n → p + e-+ 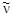 .
.
Энергия Qβ, освобождаемая при β-распаде нейтрона, выделяется в виде кинетической энергии образовавшихся частиц:
Qβ = Т = mn – mp – me - mν = mn – mp – me,
т.к. по современным представлениям mν < 18 эВ и ей можно пренебречь. Тогда
Т = mn – mp – me = 938,28 – 936,99 – 0,511 = 0,78 МэВ.
Задача 2.26
Как определяются энергии, освобождаемые при β--распаде, β+-распаде и К-захвате, если известны массы материнского и дочернего нуклидов и масса электрона.
Решение
а) Запишем выражение для нахождения энергии, освобождаемой при β--распаде:
Qβ- = M(A,Z) – M(A,Z+1) - me.
Прибавим к правой части и вычтем Z·me:
Qβ- = M(A,Z) – M(A,Z + 1) - me + Z·me - Z·me.
Так как масса атома
Maт(A,Z) = M(A,Z) + Z·me - ΔWe(A,Z),
где ΔWe(A,Z) – энергия связи всех атомных электронов, то
Qβ- = Maт(A,Z) – Maт(A,Z+1) + ΔWe(A,Z) - ΔWe(A,Z + 1).
Но величина |ΔWe(A,Z) - ΔWe(A,Z + 1)| по порядку величины равна энергии связи валентного электрона в атоме. Поэтому, с хорошей точностью
| Qβ- = Maт(A,Z) – Maт(A,Z + 1). | (2.26.1) |
б) Запишем выражение для нахождения энергии, освобождаемой при β+-распаде:
Qβ+ = M(A,Z) – M(A,Z - 1) - me.
Прибавив к правой части и вычитая Z·me, получим, выполняя преобразования аналогичные п. а),
| Qβ+ = Mат(A,Z) – Mат(A,Z - 1) - 2me. | (2.26.2) |
в) Запишем выражение для нахождения энергии, освобождаемой при К-захвате:
QК = M(A,Z) + me – M(A,Z-1).
Прибавим к правой части и вычтем (Z - 1)·me. Выполнив преобразования, аналогичные п. а), получим
| QK = Mат(A,Z) – Mат(A,Z - 1). | (2.26.3) |
Задача 2.27
Зная массу дочернего нуклида и энергию β-распада Qβ, найти массу нуклида:
а) 6Не, испытывающего β--распад, Qβ = 3,50 МэВ;
б) 22Na, испытывающего β+-распад, Qβ = 1,83 МэВ.
Решение
а) Запишем схему распада 6Не:
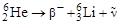 .
.
Используя формулу (2.26.1), получим
Maт(A,Z) = Maт(A,Z+1) + Qβ =
= 6 + 0,015126 + 3,50/931,5 = 6,0189 а.е.м.
б) Запишем схему распада 22Na:
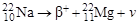 .
.
Используя формулу (2.26.2), получим
Maт(A,Z) = Maт(A,Z-1) + 2me + Qβ - =
= 22 - 0,005565 + (2·0,511 + 3,50)/931,5 = 21,99944 а.е.м.
Задача 2.28
Установить, возможны ли следующие процессы:
а) β--распад ядер 51V (-0,05602);
б) β+-распад ядер 39Са (-0,02929);
в) К-захват для ядер 63Zn (-0,06679).
В скобках указаны избытки масс нуклидов в а.е.м.
Решение
Перечисленные процессы возможны, если энергия распада Qβ > 0. Для нахождения Qβ воспользуемся результатами решения задачи 2.26.
а). По формуле (2.26.1)
| Qβ- = Maт(51V) – Ma(51Cr) = 51 + Δ(51V) – 51 - Δ(51Cr) = -0,05602 + 0,055214 < 0; нет. |
б). По формуле (2.26.2)
| Qβ+ = Mат(39Са) – Mат(39К) - 2me = 39 + Δ(39Са) – 39 - Δ(39К) – - 2me = -0,02929 + 0,036286 –2·5,486·10-4 = 5,89·10-3 > 0; да. |
в). По формуле (2.26.3)
| QK = Mат(63Zn) – Mат(63Cu) = 61 + (63Zn) – 61 - Δ(63Cu) = (-0,06679 + 0,070406) > 0; да. |
Задача 2.29
Ядро 32Р испытало β-распад, в результате которого дочернее ядро оказалось непосредственно в основном состоянии. Определить максимальную кинетическую энергию β-частиц и соответствующую кинетическую энергию дочернего ядра.
Решение
Процесс β-распада 32Р выглядит следующим образом:
32Р →β- + 32Si + 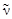 , Qβ = 1,71 МэВ (см. табл. 1 Приложений).
, Qβ = 1,71 МэВ (см. табл. 1 Приложений).
Высвобождаемая энергия в этом процессе представляется в следующим виде:
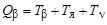 .
.
Вылету β-частиц с максимальной кинетической энергией соответствует нулевая энергии антинейтрино и для этого случая
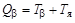 ; ;
| (2.29.1) |
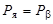 , ,
| (2.29.2) |
если материнское ядро покоится. Здесь 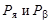 - величины импульсов дочернего ядра и β-частицы. Так как кинетическая энергия β-частиц сравнима с энергией массы покоя электрона (me = 0,511 МэВ), то кинетическая энергия β-частиц
- величины импульсов дочернего ядра и β-частицы. Так как кинетическая энергия β-частиц сравнима с энергией массы покоя электрона (me = 0,511 МэВ), то кинетическая энергия β-частиц
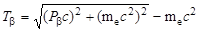 . .
| (2.29.3) |
Возведя в квадрат (2.29.2) получим
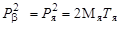 . .
| (2.29.4) |
Подставив (2.29.4) в (2.29.3), а затем полученное выражение в (2.29.1), получим уравнение для нахождения Тя:
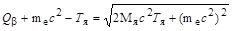 . .
| (2.29.5) |
Уравнение (2.29.5) приводится к квадратному уравнению, решение которого может быть получено обычным способом. Однако выражение решения очень громоздкое. Воспользуемся тем обстоятельством, что Тя << Q + mec2, и величиной Тя в левой части уравнения (2.29.5) можно пренебречь. Тогда
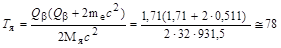 эВ. эВ.
|
Подставив полученное значение Тя в левую часть уравнения (2.29.5) из правой части этого уравнения можно найти более точное значение Тя. Предлагаем читателю убедиться, что оно будет мало отличаться от полученного выше. Точное значение Тя = 76,5 эВ.
Задача 2.30
Вычислить энергию γ-квантов, сопровождающих β-распад ядер 28Al (см. рис. 2.30.1).
Решение
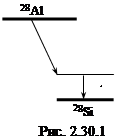 Согласно диаграмме распада дочернее ядро 28Si всегда рождается в возбужденном состоянии. Энергия возбуждения дочернего ядра будет равна
Согласно диаграмме распада дочернее ядро 28Si всегда рождается в возбужденном состоянии. Энергия возбуждения дочернего ядра будет равна
Евозб = [Δ(28Al) – Δ(28Si)]·931,5 – (Tβ)max =
= [0,023073 – 0,018092]·931,5 – 2,86 =
= 1,78 МэВ,
где (Tβ)max = 2,86 МэВ (см. табл. 1 Приложений) – максимальная энергия β-спектра.
С хорошей точностью можно считать, что энергия γ-квантов
Еγ = Евозб = 1,78 МэВ.
Задача 2.31
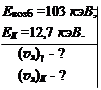 Изомерное ядро 81Sem с энергией возбуждения 103 кэВ переходит в основное состояние, испуская или γ-квант, или конверсионный электрон с К‑оболочки (энергия связи К-электрона 12,7 кэВ). Найти скорость ядра отдачи в обоих случаях.
Изомерное ядро 81Sem с энергией возбуждения 103 кэВ переходит в основное состояние, испуская или γ-квант, или конверсионный электрон с К‑оболочки (энергия связи К-электрона 12,7 кэВ). Найти скорость ядра отдачи в обоих случаях.
Решение
Скорость ядра отдачи 81Se в обоих случаях можно найти, если известен его импульс
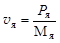 . .
| (2.31.1) |
Закон сохранения энергии и импульса при радиоактивном преобразовании ядра 81Sem в 81Se выражается следующей системой уравнений:
| Евозб = Еγ + Тя; | (2.31.2) |
| Рγ = Ря, => Еγ = Ря·c. | (2.31.3) |
Учитывая, что Тя = 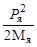 , из этой системы получим
, из этой системы получим
Евозб = Ря·(с 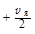 ). ).
| (2.31.4) |
Пренебрегая в (2.31.4) скоростью ядра отдачи по сравнению со скоростью света, имеем
 . .
|
Подставив полученное выражение для Ря в (2.31.1) находим
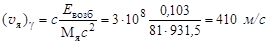 .
.
Закон сохранения энергии и импульса для явления внутренней конверсии записывается в виде
| Te = Евозб – ЕК - Тя; | (2.31.5) |
| Ре = Ря. | (2.31.6) |
Связь между кинетической энергией конверсионного электрона и его импульсом следующая:
Te = 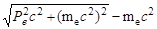 , ,
|
или, если учесть (2.30.6) то
Te = 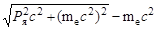 . .
|
Подставляя это выражение в (2.31.5) и выполнив несложные преобразования получим:
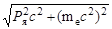 = Евозб – ЕК - Тя + mec2. = Евозб – ЕК - Тя + mec2.
| (2.31.7) |
Величиной Тя в (2.30.7) можно пренебречь. Тогда
(vя)К = 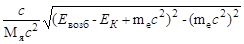 =
= =
= 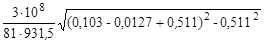 = 1,26·103 м/с. = 1,26·103 м/с.
|
Задача 2.32
 Свободное ядро с энергией возбуждения Евозб = 129 кэВ переходит в основное состояние, испустив γ-квант. Найти изменение энергии γ-кванта относительно энергии возбуждения вследствие отдачи ядра.
Свободное ядро с энергией возбуждения Евозб = 129 кэВ переходит в основное состояние, испустив γ-квант. Найти изменение энергии γ-кванта относительно энергии возбуждения вследствие отдачи ядра.
Решение
По закону сохранения энергии и импульса
| Евозб = Еγ + Тя; | (2.32.1) |
| Рγ = Ря, => Еγ = Ря·c. | (2.32.2) |
Из этих уравнений
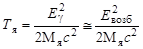 . .
| (2.32.3) |
Подставляя (2.32.3) в (2.32.1), получим
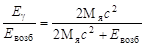 .
.
Поэтому, относительное изменение энергии γ-кванта
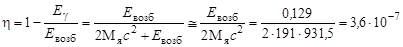 .
.
Задача 2.33
С какой скоростью должны сближаться источник и поглотитель, состоящие из свободных ядер 191Ir, чтобы можно было наблюдать максимальное поглощение γ-квантов с энергией 129 кэВ.
Решение
Максимальное (резонансное) поглощение γ-квантов может наблюдаться только тогда, когда γ-квант передает ядру энергию, равную энергии возбуждения Евозб. Но γ-квант уносит не всю энергию Евозб возбуждения ядра, так как часть этой энергии Тя передается на отдачу ядра, испустившего γ-квант:
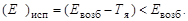
Для возбуждения ядра до энергии Евозб нужно поглотить g-квант с энергией
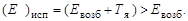
так как согласно закону сохранения импульса часть энергия g-кванта превращается в кинетическую энергию движения ядра. В результате энергии испущенного и поглощенного g-квантов не совпадают на величину 2Тя и для наблюдения максимального (резонансного) поглощения необходимо чтобы излучающие и поглощающие ядра имели кинетическую энергию относительного движения, равную 2Тя.
Согласно решению предыдущей задачи (см. формулу (2.32.3))
2Тя = 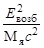 ,
,
а относительная скорость сближения источника и поглотителя равна
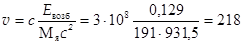 м/с.
м/с.
Дата добавления: 2016-06-13; просмотров: 15290;
