Уровни ядер. Сечения и выходы ядерных реакций
Задача 3.17
Найти энергию возбуждения покоящегося ядра массой Мя, которую оно получит при захвате γ-кванта с энергией Еγ.
Решение.
Из закона сохранения импульса следует, что неподвижное ядро после поглощения γ-кванта начнет движение с кинетической энергией (см. (2.32.3))
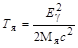 ,
,
а энергия возбуждения составит
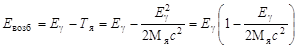 .
.
Задача 3.18
 Определить Евозб - энергию возбуждения ядра 4Не, возникшего в результате захвата протона с кинетической энергией 2,0 МэВ покоящимся ядром 3Н.
Определить Евозб - энергию возбуждения ядра 4Не, возникшего в результате захвата протона с кинетической энергией 2,0 МэВ покоящимся ядром 3Н.
Решение
Согласно формуле (3.4)


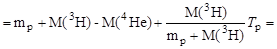
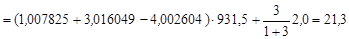 МэВ.
МэВ.
Задача 3.19
Какой минимальной кинетической энергией (Тn)min должен обладать нейтрон, чтобы в результате упругого рассеяния на ядре 9Ве сообщить последнему энергию возбуждения Евозб= 2,40 МэВ.
Решение
Запишем закон сохранения энергии для неупругого рассеяния:
| Тn = Т2 + Евозб, | (3.19.1) |
где Т2 –суммарная кинетическая энергия частиц после рассеяния;
и закон сохранения импульса:
 , ,
| (3.19.2) |
где 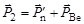 - суммарный импульс частиц после рассеяния.
- суммарный импульс частиц после рассеяния.
 Из (3.19.1) следует, что минимальная величина кинетической энергии (Тn)min налетающего нейтрона, необходимая для возбуждения ядра мишени до заданной величины Евозб, определяется минимальным значением кинетической энергии Т2, которая, в свою очередь, определяется минимально возможными величинами импульсов Рn и РВе. На рис. 3.19.1 графически изображен закон сохранения импульса, из которого следует, что минимальные величины импульсов Рn и РВе соответствуют движению частиц после рассеяния вдоль первоначального направления движения нейтрона. Для этого случая после возведения в квадрат уравнения (3.19.2), получим
Из (3.19.1) следует, что минимальная величина кинетической энергии (Тn)min налетающего нейтрона, необходимая для возбуждения ядра мишени до заданной величины Евозб, определяется минимальным значением кинетической энергии Т2, которая, в свою очередь, определяется минимально возможными величинами импульсов Рn и РВе. На рис. 3.19.1 графически изображен закон сохранения импульса, из которого следует, что минимальные величины импульсов Рn и РВе соответствуют движению частиц после рассеяния вдоль первоначального направления движения нейтрона. Для этого случая после возведения в квадрат уравнения (3.19.2), получим
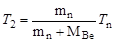 . .
| (3.19.3) |
Подставив выражение (3.19.3) в (3.19.1) имеем окончательно
(Тn)min= 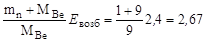 МэВ.
МэВ.
Задача 3.20
Найти кинетические энергии нейтронов, при которых сечения взаимодействия с ядрами 16О максимальны, если нижние уровни составного ядра 17О соответствуют энергиям возбуждения 0,87; 3,00; 3,80; 4,54; 5,07 и 5,36 МэВ.
Решение
 В предлагаемой задаче речь идет о резонансном характере зависимости сечения (рис. 3.20.1) ядерной реакции радиационного захвата (n,γ) от кинетической энергии нейтронов, захватываемых ядром 16О с образованием возбужденного составного ядра 17О. При захвате нейтрона ядром 16О в энергию возбуждения составного ядра 17О может быть передана, согласно (3.4), энергия
В предлагаемой задаче речь идет о резонансном характере зависимости сечения (рис. 3.20.1) ядерной реакции радиационного захвата (n,γ) от кинетической энергии нейтронов, захватываемых ядром 16О с образованием возбужденного составного ядра 17О. При захвате нейтрона ядром 16О в энергию возбуждения составного ядра 17О может быть передана, согласно (3.4), энергия
 . .
| (3.20.1) |
Если эта энергия равна энергии Евозб одного из уровней возбуждения составного ядра, то реакция протекает наиболее вероятно и ее сечение резко возрастает. Поэтому
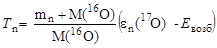 . .
| (3.20.2) |
Вычислим энергию связи нейтрона относительно составного ядра 17О:
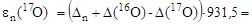
 931,5 = 4,14 МэВ. 931,5 = 4,14 МэВ.
| (3.20.3) |
Из сравнения (3.20.3) и (3.20.1) следует, что энергия возбуждения составного ядра должна быть не меньше 4,14 МэВ. Следовательно, первые три нижних уровня энергии возбуждения ядра 17О: - 0,87; 3,00 и 3,80 МэВ не могут быть связаны с захватом нейтрона ядром 16О, а являются вращательными уровнями (ядро 17О имеет сплюснутую форму, т.к. его квадрупольный момент Q < 0) и заселяются другим образом, например, при захвате γ-кванта. Вычисления кинетической энергии Тn нейтронов по формуле (3.20.2) для энергий возбуждения 4,54; 5,07 и 5,36 МэВ и 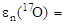 4,14 МэВ дают следующие результаты: 0,34; 0,99 и 1,30 МэВ.
4,14 МэВ дают следующие результаты: 0,34; 0,99 и 1,30 МэВ.
Задача 3.21
 Определить среднее время жизни ядер, возникающих при захвате нейтронов ядрами 6Li, если известно среднее время жизни данных ядер по отношению к испусканию нейтронов и α-частиц: τn = 1,1·10‑20 с и τα = 2,2·10‑20 с (других возможностей нет).
Определить среднее время жизни ядер, возникающих при захвате нейтронов ядрами 6Li, если известно среднее время жизни данных ядер по отношению к испусканию нейтронов и α-частиц: τn = 1,1·10‑20 с и τα = 2,2·10‑20 с (других возможностей нет).
Решение
Образующееся возбужденное ядро 7Li* может распадаться по двум каналам с удельными вероятностями (постоянными распада) λn и λα. Полная удельная вероятность распада ядра 7Li* составит
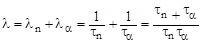 .
.
Учитывая, что λ =1/τ, получим
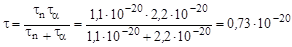 с.
с.
Задача 3.22
 Найти плотность потока нейтронов на расстоянии 10 см от небольшого Ро-Ве–источника, содержащего 0,63·1010 Бк (0,17 Ки) 210Ро, если выход реакции 9Ве(α, n)12С равен 0,8·10-4.
Найти плотность потока нейтронов на расстоянии 10 см от небольшого Ро-Ве–источника, содержащего 0,63·1010 Бк (0,17 Ки) 210Ро, если выход реакции 9Ве(α, n)12С равен 0,8·10-4.
Решение
По определению плотность потока частиц есть отношение числа частиц 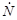 , поступающих внутрь объема сферы в единицу времени, отнесенное к площади S диаметрального сечения этой сферы:
, поступающих внутрь объема сферы в единицу времени, отнесенное к площади S диаметрального сечения этой сферы:
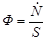 . .
| (3.22.1) |
Примем, что на расстоянии R = 10 см размерами источника можно пренебречь и считать его точечным излучателем. Пусть источник  испускает изотропно
испускает изотропно 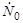 нейтронов в одну секунду. Тогда (см. рис. 3.22.1) в сферу бесконечно малого объема, находящуюся на расстоянии R от точечного источника О, будет поступать
нейтронов в одну секунду. Тогда (см. рис. 3.22.1) в сферу бесконечно малого объема, находящуюся на расстоянии R от точечного источника О, будет поступать

нейтронов в секунду. Так как по определению элемент телесного угла
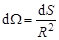 ,
,
то
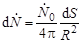 ,
,
откуда, согласно (3.22.1), плотность потока
 . .
| (3.22.1) |
Число нейтронов, испускаемых источником в секунду,
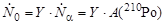 ,
,
так как при α-распаде одного ядра 210Ро возникает одна α-частица. Подставляя полученное выражение для 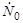 в (3.22.1), найдем плотность потока нейтронов на расстоянии 10 см от источника
в (3.22.1), найдем плотность потока нейтронов на расстоянии 10 см от источника
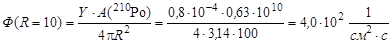 .
.
Задача 3.23
 Выход реакции (γ,n) при облучении медной пластинки толщиной d = 1,0 мм γ-квантами энергией 17 МэВ составляет Υ = 4,2·10-4. Найти сечение данной реакции.
Выход реакции (γ,n) при облучении медной пластинки толщиной d = 1,0 мм γ-квантами энергией 17 МэВ составляет Υ = 4,2·10-4. Найти сечение данной реакции.
Решение
Число реакций, происходящих в единицу времени на единичной площади мишени толщиной dx составляет
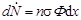 ,
,
где n - концентрация атомов меди, Ф –плотность потока γ-квантов в рассматриваемой точке мишени. Интегрируя это выражение, получим число реакций, происходящих в единицу времени на единичной площади мишени толщиной d:
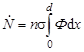 . .
| (3.23.1) |
Имеются два фактора, в результате которых плотность параллельного потока γ-квантов уменьшается по мере их движения в мишени. Это, с одной стороны, взаимодействие γ-квантоа с атомами (образование электронно-позитронных пар и комптоновское рассеяние), а, с другой стороны, уменьшение плотности потока γ-квантов за счет захвата их ядрами меди (реакция (γ,n)). Первый фактор имеет определящее значение, но средняя длина пробега γ-кванта с энергией 17 МэВ в меди до первого взаимодействия с атомом около 5 см (предлагается оценить самостоятельно), т.е. существенно превышает толщину мишени. Мишень, толщина которой много меньше средней длины пробега частиц, называется тонкой мишенью. Поэтому в (3.23.1) плотность потока γ-квантов можно положить постоянной по толщине мишени и тогда
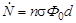 , ,
| (3.23.2) |
где Ф0 – плотность потока γ-квантов, падающих на пластинку. Тогда
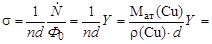
 см2 = 0,05 барн.
см2 = 0,05 барн.
Используя полученное сечение рекомендуется самостоятельно оценить среднюю длину пробега γ-кванта до первого взамодкйствия с ядром меди.
Задача 3.24
 Тонкую пластинку из 113Cd облучают тепловыми нейтронами, плотность потока которых 1,0·1012 с-1·см-2. Найти сечение реакции (n,γ), если известно, что через шесть суток облучения содержание ядер нуклида 113Cd уменьшилось на 1%.
Тонкую пластинку из 113Cd облучают тепловыми нейтронами, плотность потока которых 1,0·1012 с-1·см-2. Найти сечение реакции (n,γ), если известно, что через шесть суток облучения содержание ядер нуклида 113Cd уменьшилось на 1%.
Решение
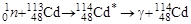 .
.
Число реакций, происходящих в единичном объеме вещества в единицу времени по определению равно
ν = nσФ.
Изменение концентрации ядер мишени за промежуток времени dt будет равно
dn = - νdt =-nσФdt.
Решение этого уравнения с начальным условием n(t=0) = n0 выражается формулой
n(t) = n0exp(-σФt),
используя которую, получаем, что
 1 - exp(-σФt).
1 - exp(-σФt).
Из последнего уравнения
 см2 = 2·104 барн.
см2 = 2·104 барн.
Задача 3.25
 При облучении дейтонами с кинетической энергией 1 МэВ тонкой мишени из тяжелого льда выход и сечение реакции 2Н(d,n)3Не равны соответственно 0,8·10-5 и 0,020 мб. Определить сечение данной реакции для кинетической энергии дейтонов 2 МэВ, если выход в этом случае составляет 4,0·10-5.
При облучении дейтонами с кинетической энергией 1 МэВ тонкой мишени из тяжелого льда выход и сечение реакции 2Н(d,n)3Не равны соответственно 0,8·10-5 и 0,020 мб. Определить сечение данной реакции для кинетической энергии дейтонов 2 МэВ, если выход в этом случае составляет 4,0·10-5.
Решение
Для тонкой мишени из формулы (3.23.3) получим выражения для выхода реакции 2Н(d,n)3Не:
 .
.
Тогда
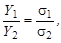
откуда
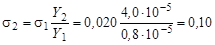 б.
б.
Задача 3.26
При облучении толстой☼ алюминиевой мишени пучком α-частиц с энергией 7,0 МэВ в результате реакции (α,n) испускается поток нейтронов 1,60·109 с-1. Найти выход и среднее сечение данной реакции, если ток α-частиц равен 50 мкА.
Решение
Число нейтронов, образующихся в слое мишени толщиной dx в единицу времени, будет равно
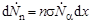 ,
,
где: n - концентрация ядер мишени; 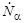 - количество α-частиц. падающих на мишень в единицу времени; σ – сечение данной реакции.
- количество α-частиц. падающих на мишень в единицу времени; σ – сечение данной реакции.
При движении в мишени α-частицы испытывают ионизационное торможение, взаимодействуя с электронными оболочками атомов, но их общее количество фактически не уменьшается, так как потерями α-частиц из-за взаимодействия с ядрами мишени можно пренебречь (выход реакции Υ << 1). Поэтому уменьшается только их кинетическая энергия по мере движения в мишени и, следовательно, изменяется сечение реакции, т.е. σ = σ(х). На всем пути α-частицы произведут число нейтронов
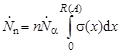 , ,
| (3.26.1) |
где R(A) – пробег α-частиц с начальной кинетической энергией 7 МэВ в веществе мишени с массовым числом А.
Выход реакции равен по определению
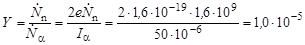 ,
,
так как ток α-частиц Iα= 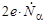 .
.
Таким образом, (3.26.1) можно записать в виде
 . .
| (3.26.2) |
Используя теорему интегрального исчисления о среднем значении подынтегральной функции, из выражения (3.26.2) получаем
 . .
| (3.26.3) |
Для определения средней длины R(А) пробега α-частиц c кинетической энергией Т используем эмпирические формулы для нахождения пробега α-частиц:
а) в воздухе
Rвозд =0,31T3/2 =0,31·73/2 = 5,7 см;
б) а затем в веществе с массовым числом А
Rm(A) = R(A)·ρ= 0,56·A1/3·Rвозд = 0,56·271/3·5,7 = 9,6 мг/см2,
где ρ – плотность вещества мишени. Величина Rm носит название массового пробега.
Подставив полученные величины в формулу (3.26.3), получим

Дата добавления: 2016-06-13; просмотров: 3963;
