Деление и синтез ядер

Задача 5.1

Определить:

а) энергию, выделяющуюся при делении ядер («сгорании») m = 1 кг ²³⁵U; какая масса нефти М_неф с теплотворной способностью q_неф = 42 кДж/г выделяет при сгорании такую энергию?

б) среднюю электрическую мощность атомной электростанции, если расход нуклида ²³⁵U за время t = 1 год составляет М =192 кг при к.п.д. η = 30%;

в) массу нуклида ²³⁵U, подвергшуюся делению при взрыве атомной бомбы с тротиловым эквивалентом Е_тр = 30 кт, если теплой эквивалент тротила q_тр = 4,1 кДж/г.

Решение

а) Примем, что при делении одного ядра нуклида ²³⁵U выделяется энергия Q = 200 МэВ. Тогда деление массы m = 1 кг ²³⁵U приведет к выделению энергии

,

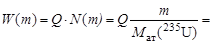
(5.1.1)

где N(m) – количество атомов в одном килограмме ²³⁵U. Масса нефти, которая потребуется для получения такого количества энергии, составит

.

б) Средняя за год мощность атомной электростанции составит

.

в) Масса нуклида ²³⁵U, испытавшего деление, составит

.

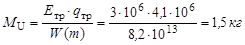Задача 5.2

Ядро ²³⁵U захватило тепловой нейтрон. В результате деления образовавшегося составного ядра возникло три нейтрона и два радиоактивных осколка, которые превратились в стабильные ядра ⁸⁹Y и ¹⁴⁴Nb . Найти энергию, освободившуюся в этом процессе, если известны:

а) избытки масс нейтрона и ядер ²³⁵U, ⁸⁹Y (-0, 09415а.е.м.) и ¹⁴⁴Nb (-0,09010 а.е.м.);

б) энергии связи на один нуклон в ядрах ²³⁵U (7,59 МэВ), ⁸⁹Y (8,71 МэВ), ¹⁴⁴Nb (8,32 МэВ) и энергия связи нейтрона в ядре ²³⁶U (6,40 МэВ).

Решение

а)В терминах избытка масс выделенная энергия

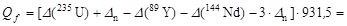
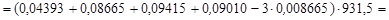
= 196,4 МэВ.

б) В терминах энергии связи выделяемая энергия равна увеличению энергии связи системы, т.е. разности энергии связи между конечной и исходной системой. При этом необходимо учесть, что на составном этапе образуется составное ядро ²³⁶U, которое возбуждено и энергия возбуждения Е_возб выделяется при делении составного ядра. Тогда

,

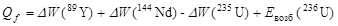где энергия возбуждения составного ядра ²³⁶U

.

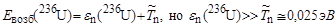Следовательно

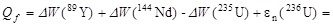
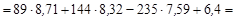196 МэВ.

Задача 5.3

Ядро, возникающее при захвате нейтрона ядром ²³⁸U, испытывает деление, если кинетическая энергия нейтрона превышает 1,4 МэВ. Найти энергию активации делящегося ядра.

Решение

При захвате ядром ²³⁸U нейтрона возникает возбужденное составное ядро ²³⁹U. Деление составного ядра ²³⁹U может произойти только тогда, когда энергия его возбуждения Е_возб превышает энергию активации Е_акт, т.е.

.

Из этого соотношения

.

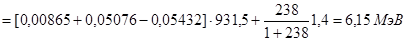Задача 5.4

Определить наиболее вероятную и среднюю кинетическую энергию вторичных нейтронов деления ядер ²³⁵U при захвате нейтронов. Энергетический спектр вторичных нейтронов деления имеет вид: , где А – нормировочная константа; T_n - кинетическая энергия вторичных нейтронов деления, МэВ.

Решение

Наиболее вероятная кинетическая энергия (T_n)_вер вторичных нейтронов деления соответствует энергии, при которой наблюдается максимум энергетического распределения вторичных нейтронов деления. Дифференцируя заданное распределение по энергии, и приравнивая его нулю при T_n = (T_n)_вер, получим уравнение для нахождения (T_n)_вер:

.

Из последнего уравнения

.

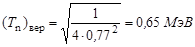Среднее по энергетическому спектру значение кинетической энергии 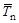вторичных нейтронов деления находим обычным образом по правилу нахождения среднего значения случайной величины:

.

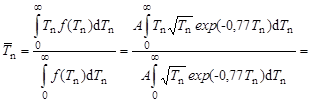
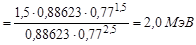Вычисление интегралов рекомендуется выполнить самостоятельно. Значения определенных интегралов выражаются посредством соответствующих гамма-функций.

Задача 5.5

Вычислить среднее сечение деления 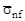на ядро урана природного изотопного состава для тепловых нейтронов.

Решение

Тепловыми нейтронами делятся только ядра нуклида ²³⁵U, атомное содержание которого в природном уране составляет 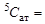0,714%. Очевидно, что должны быть равны соответствующие макроскопические сечения (почему?)

,

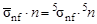где 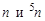- концентрации ядер природного урана и нуклида ²³⁵U; 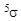- сечение деления ядер ²³⁵U тепловыми нейтронами. Тогда

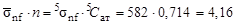барн.

Значение сечения деления 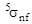взяты из таблиц Приложения.

Задача 5.6

Вычислить долю тепловых нейтронов, захват которых ядрами ²³³U, ²³⁵U и ²³⁹Pu, сопровождается делением.

Решение

Захват теплового нейтрона ядрами, перечисленными в условии задачи, еще не означает, что ядро обязательно разделится. Образовавшееся возбужденное составное ядро может перейти в основное состояние, испустив γ-квант. Поэтому радиационный захват является процессом, который конкурирует с делением составного ядра. Доля тепловых нейтронов, вызывающих деление, равна

,

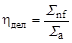(5.6.1)

где 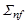и 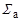- макроскопические сечения деления и захвата нейтронов соответственно. Для среды, состоящей из одного нуклида, из 5.6.1 получим

.

В итоге, используя данные по сечениям из таблиц Приложения, получим:

для ²³³U

;

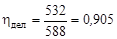для ²³⁵U

;

для ²³⁹Pu

.

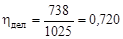Задача 5.7

Найти средние числа вторичных нейтронов деления на один поглощенный тепловой нейтрон ядрами ²³³U, ²³⁵U и ²³⁹Pu.

Решение

,

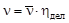(5.7.1)

где 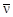- среднее число вторичных нейтронов при делении соответствующего ядра, приведенные в таблицах Приложения.

В итоге из формулы (5.7.1) и результатов задачи 5.6.1 получим:

для ²³³U

;

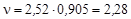для ²³⁵U

;

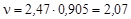для ²³⁹Pu

.

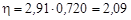Задача 5.8

Сравнить среднее число мгновенных нейтронов деления на один поглощенный тепловой нейтрон в естественном и обогащенном (1,5% ²³⁵U) уране.

Решение

Для решения следует воспользоваться формулами (5.6.1) и (5.7.1). Макроскопическое сечение поглощения нейтрона 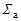, входящее в формулу (5.6.1), теперь определяется как

,

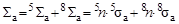поскольку тепловые нейтроны поглощаются не только ядрами ²³⁵U, но и ядрами ²³⁸U, в результате чего доля тепловых нейтронов, вызывающих деление, уменьшается. Подставив это выражение в формулу (5.6.1), получим

,

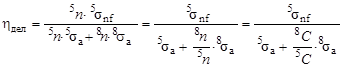где 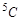и 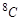- атомные содержания ²³⁵U и ²³⁸U в делящемся материале. Используя формулу (5.7.1) для выражение 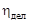, получаем рабочую формулу для нахождения :

.

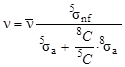Для урана естественного изотопного состава

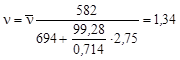
Для урана, обогащенного до 1,5% нуклидом ²³⁵U

.

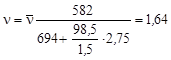Из полученного результата следует, что цепной процесс деления тепловыми нейтронами можно осуществить на уране природного изотопного состава, если в процессе замедления вторичных нейтронов терять, в среднем, не более 0,3 количества вторичных нейтрона нов на один поглощенный нейтрон.

Задача 5.9

Реактор на тепловых нейтронах, в котором делящимся нуклидом является ²³⁵U, работает на постоянном уровне мощности. Найти долю нейтронов 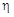, захватываемых без деления ядрами урана и примесей, если доля нейтронов f, покидающих активную зону, составляет 10%.

Решение

Обозначим как N₁ число нейтронов предыдущего цикла обращения (поколения), а через N₂ – число нейтронов последующего цикла обращения. По условию задачи N₁ = N₂. Но

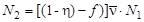
или

,

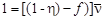т.к. N₁ = N₂. Выражение в квадратных скобках есть доля тепловых нейтронов, вызывающих деление. Тогда

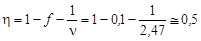
Задача 5.10

Какой слой чистого ²³⁵U при нормальном падении тепловых нейтронов дает в среднем один вторичный нейтрон деления на каждый падающий первичный.

Решение

Пусть на пластинку падает - тепловых нейтронов в секунду. После прохождения слоя урана толщиной 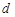количество тепловых нейтронов, которые не испытали захвата ядрами ²³⁵U, составит

,

где 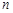– концентрация ядер ²³⁵U, а 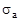- сечение захвата тепловых нейтронов ядрами ²³⁵U. Число тепловых нейтронов в секунду, которые испытали захват, будет равно

.

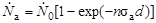Если эту величину умножить на среднее число вторичных нейтронов деления , возникающих при захвате одного теплового нейтрона (см. формулу (5.6.2) в задаче 5.6 и формулу (5.7.1) в задаче 5.7), то получим число 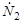быстрых нейтронов, возникающих в секунду в результате деления ядер ²³⁵U:

.

Так как по условию задачи 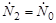, то уравнение для нахождения толщины слоя d:

,

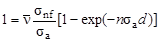из которого

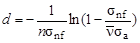= 0,2 мм.

Численные расчеты выполнить самостоятельно.

Задача 5.11

Оценить энергетические ресурсы одного литра воды в отношении реакций синтеза на дейтерии и определить количество бензина с теплотворной способностью q = 42 кДж/г, которое выделяет при сгорании такое количество энергии. Считать, что атомное содержание дейтерия составляет 0,015% по отношению к атомам протия.

Решение

Будем учитывать следующие две реакции под действием дейтонов

и считать, что обеспечены условия, при которых весь образующийся тритий участвует в реакции.

Полагая равной вероятность обоих каналов реакции (d-d), получим, что в реакции (d-t) может участвовать одна пятая часть первоначального количества ядер дейтерия. Тогда энергия возможного синтеза ядер дейтерия в одном литре воды составит

,

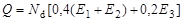(5.11.1)

где 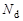- количество ядер дейтерия, содержащихся в одном литре воды; Е₁ и Е₂ – энергия, выделяемая в верхнем и нижнем каналах реакции d-d; Е₃ – энергия реакции d-t.

Полагая плотность воды равной 1 кг/л, найдем

.

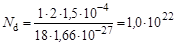Энергии соответствующих реакций равны:

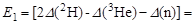
МэВ.

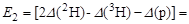
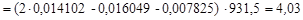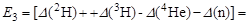
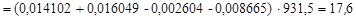МэВ.

МэВ.

Подставив полученные данные в (5.11.1) определим

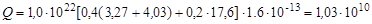Дж.

Тогда масса бензина, дающая такое же количество энергии при сгорании, составит

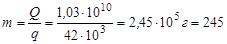кг.

Задача 5.12

По современным представлениям источником энергии звезд являются реакции слияния (синтеза) легких ядер. На Солнце протекает т.н. водородный цикл, в результате которого из четырех протонов образуется ядро ⁴Не, два позитрона и два нейтрино:

,

.

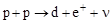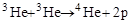Первые две реакции входят в полный цикл дважды.

Вычислить энергию, выделяющуюся в этом цикле.

Решение

Сложив отдельно левые и правые части уравнений реакций, получим

.

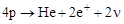Освобождаемая при этом энергия

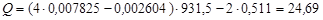МэВ.

В результате последующей аннигиляции двух позитронов с двумя электронами выделяется еще 4·0511 = 2,044 МэВ и полный выход энергии составит 26,73 МэВ, из которых 0,514 МэВ (~ 2%) безвозвратно уносят два нейтрино из дважды повторяемой первой реакции цикла.

[1] Зеркальными называются ядра изобар, у которых число протонов одного из ядер равно числу нейтронов у другого.

☼ Толстой называют мишень, толщина которой больше пробега в ней бомбардирующих частиц.