Законы сохранения в ядерных реакциях
Задача 3.1
 α-Частица с кинетической энергией Тα = 1,0 МэВ упруго рассеялась на покоящемся ядре 6Li. Определить кинетическую энергию ядра отдачи, отлетевшего под углом φ = 30º к первоначальному направлению движения α-частицы.
α-Частица с кинетической энергией Тα = 1,0 МэВ упруго рассеялась на покоящемся ядре 6Li. Определить кинетическую энергию ядра отдачи, отлетевшего под углом φ = 30º к первоначальному направлению движения α-частицы.
Решение
Запишем законы сохранения энергии и импульса для упругого рассеяния:
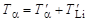 ; ;
| (3.1.1) |
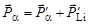 . .
| (3.1.2) |
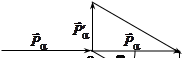 Изобразим графически закон сохранения импульса для процесса упругого рассеяния α-частицы на покоившимся ядре 6Li, которое произошло в точке «о». Верхние правые индексы « ' » обозначают величины после рассеяния.
Изобразим графически закон сохранения импульса для процесса упругого рассеяния α-частицы на покоившимся ядре 6Li, которое произошло в точке «о». Верхние правые индексы « ' » обозначают величины после рассеяния.
По теореме косинусов
 . .
| (3.1.3) |
Так как энергия покоя α-частиц mαс2 >> Тα, то можно использовать классическую связь между импульсом и кинетической энергий. Тогда (3.1.3) приобретает вид:
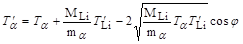 . .
| (3.1.4) |
Выразим 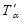 из (3.1.1), подставим в уравнение (3.1.4) и, освободившись от иррациональности, получим
из (3.1.1), подставим в уравнение (3.1.4) и, освободившись от иррациональности, получим
 . .
| (3.1.5) |
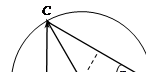 Эта же задача может быть решена с помощью векторной диаграммы импульсов для упругого рассеяния, построение которой приведено на рис. 3.2. Построение векторной диаграммы импульсов для поставленной задачи изображено на рисунке слева. Энергия ядра 6Li после соударения выражается через его импульс следующим образом
Эта же задача может быть решена с помощью векторной диаграммы импульсов для упругого рассеяния, построение которой приведено на рис. 3.2. Построение векторной диаграммы импульсов для поставленной задачи изображено на рисунке слева. Энергия ядра 6Li после соударения выражается через его импульс следующим образом
 . .
| (3.1.6) |
Но длина отрезка CB соответствует величине импульса 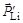 . Для нахождения отрезка CB используем равнобедренный треугольник COВ:
. Для нахождения отрезка CB используем равнобедренный треугольник COВ:
СВ = 2ОВ·cosφ.
Тогда
 .
.
Подставляя последнее выражение в (3.1.6), получим окончательно
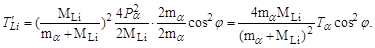
|
Полученное выражение для энергии 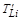 полностью совпадает с выражением (3.1.5), но получено гораздо проще, что, в конечном итоге, оправдывает применение векторной диаграммы импульсов.
полностью совпадает с выражением (3.1.5), но получено гораздо проще, что, в конечном итоге, оправдывает применение векторной диаграммы импульсов.
Задача 3.2
 Нерелятивистский дейтон упруго рассеялся на покоящемся ядре под углом 30º. Под таким же углом к направлению движения налетающего дейтона отлетело и ядро отдачи. Какому нуклиду принадлежит это ядро?
Нерелятивистский дейтон упруго рассеялся на покоящемся ядре под углом 30º. Под таким же углом к направлению движения налетающего дейтона отлетело и ядро отдачи. Какому нуклиду принадлежит это ядро?
Решение
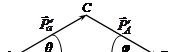 Рассмотрение кинематики упругого рассеяния позволяет определить только массовое число ядра.
Рассмотрение кинематики упругого рассеяния позволяет определить только массовое число ядра.
Изобразим графически закон сохранения импульса. Из равнобедренного треугольника АВС находим, что
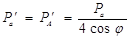 .
.
Подставляя полученные значения импульсов в закон сохранения энергии (3.1.1), получим
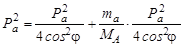 ,
,
откуда
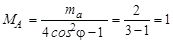 а.е.м.
а.е.м.
Рассеяние ядра дейтерия произошло на протоне (ядре протия).
Задача 3.3
Построить векторные диаграммы импульсов для упругого рассеяния нерелятивистской α-частицы на покоящемся ядре:
а) 6Li, 4Не, 2Н, если угол рассеяния в α-частицы в СЦИ равен 60º. В каком случае связь между кинетической энергией рассеянной α-частицы и углом ее рассеяния неоднозначна? Найти для этих трех случаев значения максимально возможного угла рассеяния α-частицы.
Решение
Для анализа упругого рассеяния α-частицы построим векторные диаграммы импульсов для всех трех случаев.
а) рассеяние α-частицы на ядре 6Li.
 Отрезок АВ, изображающий импульс налетающей α-частицы, делим на 5 равных частей, т.к. mα : M(6Li) = 2 : 3. От точки А отсчитываем две части и ставим точку О. Из точки О радиусом ОВ проводим дугу ВD. Под углом
Отрезок АВ, изображающий импульс налетающей α-частицы, делим на 5 равных частей, т.к. mα : M(6Li) = 2 : 3. От точки А отсчитываем две части и ставим точку О. Из точки О радиусом ОВ проводим дугу ВD. Под углом  = 60º из точки О проводим луч до пересечения с дугой ВD. Точку пересечения обозначаем буквой С и соединяем ее с точками А и В. Полученный отрезок АС и угол
= 60º из точки О проводим луч до пересечения с дугой ВD. Точку пересечения обозначаем буквой С и соединяем ее с точками А и В. Полученный отрезок АС и угол  изображают величину импульса α-частицы и направление ее движения после рассеяния в ЛСК, а отрезок СВ – и угол φ величину импульс ядра и направление движения ядра 6Li после соударения также в ЛСК. Для различных параметров удара точка С может располагаться на дуге ВD в любом месте от точки B и до точки D. При этом величина импульса α-частицы после рассеяния (длина отрезка АС) однозначно связана с углом
изображают величину импульса α-частицы и направление ее движения после рассеяния в ЛСК, а отрезок СВ – и угол φ величину импульс ядра и направление движения ядра 6Li после соударения также в ЛСК. Для различных параметров удара точка С может располагаться на дуге ВD в любом месте от точки B и до точки D. При этом величина импульса α-частицы после рассеяния (длина отрезка АС) однозначно связана с углом  или углом
или углом 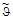 . Следовательно и кинетическая энергия T = P2/2m в этом случае является однозначной функцией угла рассеяния а обеих системах координат. Максимальные углы рассеяния
. Следовательно и кинетическая энергия T = P2/2m в этом случае является однозначной функцией угла рассеяния а обеих системах координат. Максимальные углы рассеяния 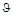 и
и 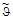 в этом случае определяются положением точки С при ее совпадении с точкой D и равны π.
в этом случае определяются положением точки С при ее совпадении с точкой D и равны π.
б) Рассеяние α-частицы на ядре 4Не.
 Так как массы сталкивающихся частиц равны, то отрезок АВ делим на две равные части и проводим дугу ВD с центром в точке О. Далее построения не отличаются от построений в предыдущем пункте задачи. В этом случае связь кинетической энергии рассеянной α-частицы с углами рассеяния оказывается также однозначной в обеих системах координат. Предельное значение угла
Так как массы сталкивающихся частиц равны, то отрезок АВ делим на две равные части и проводим дугу ВD с центром в точке О. Далее построения не отличаются от построений в предыдущем пункте задачи. В этом случае связь кинетической энергии рассеянной α-частицы с углами рассеяния оказывается также однозначной в обеих системах координат. Предельное значение угла 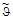 также стремиться к π. Однако, как нетрудно заметить, предельное значение угла
также стремиться к π. Однако, как нетрудно заметить, предельное значение угла 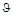 стремиться к π/2. Из этого следует важный вывод о том, что угол рассеяния двух тел с одинаковой массой не может превышать π/2.
стремиться к π/2. Из этого следует важный вывод о том, что угол рассеяния двух тел с одинаковой массой не может превышать π/2.
в) рассеяние α-частицы на ядре 2Н.
Отрезок АВ, изображающий импульс налетающей α-частицы, делим на 3 равных части, т.к. mα : M(2Н) = 2 : 1. От точки А отсчитываем две части и ставим точку О. Далее построения не отличаются от построений в предыдущих пунктах а) и б). Из диаграммы следует, что одному значению угла 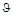 рассеяния в ЛСК соответствуют две возможные величины импульса рассеянной α-частицы (отрезки AD и АС), а, следовательно, и два возможных значения кинетической энергии рассеянной α-частицы. Максимальное значение угла
рассеяния в ЛСК соответствуют две возможные величины импульса рассеянной α-частицы (отрезки AD и АС), а, следовательно, и два возможных значения кинетической энергии рассеянной α-частицы. Максимальное значение угла 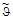 рассеяния α-частицы в СЦИ будет равно π. В ЛСК максимальное значение угла
рассеяния α-частицы в СЦИ будет равно π. В ЛСК максимальное значение угла 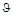 определяется положением касательной
определяется положением касательной 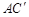 . Из прямоугольного треугольника
. Из прямоугольного треугольника  сразу следует, что
сразу следует, что

и, следовательно,
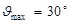 .
.
Задача 3.4
Какую долю η кинетической энергии теряет нерелятивистская α-частица при упругом рассеянии под углом 60º в СЦИ на покоящимся ядре 12С.
Решение
 Построим векторную диаграмму импульсов. Отрезок АВ, изображающий импульс налетающей α-частицы, делим на 4 равных части, т.к. mα : M(12С) = 1 : 3. От точки А отсчитываем одну часть и ставим точку О. Далее построения не отличаются от построений в предыдущей задачи.
Построим векторную диаграмму импульсов. Отрезок АВ, изображающий импульс налетающей α-частицы, делим на 4 равных части, т.к. mα : M(12С) = 1 : 3. От точки А отсчитываем одну часть и ставим точку О. Далее построения не отличаются от построений в предыдущей задачи.
Искомая доля будет равна
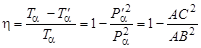 .
.
Из треугольника АОС, используя теорему косинусов, находим
АС2 = 1 + 9 – 2·1·3·cos(π - 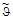 ) = 1 + 9 + 3 = 13.
) = 1 + 9 + 3 = 13.
Тогда
 .
.
Рекомендуется получить формулу для вычисления η.
Задача 3.5
 Найти энергию реакции 7Li(p, α)4He, если известно, что удельная энергия связи в ядрах 7Li и 4He равна соответственно 5,50 и 7,06 МэВ.
Найти энергию реакции 7Li(p, α)4He, если известно, что удельная энергия связи в ядрах 7Li и 4He равна соответственно 5,50 и 7,06 МэВ.
Решение
Согласно (3.2)
Q = M(7Li) + mp- 2М(4Не).
Используя формулу для полной энергии связи ядра:
ΔW(A,Z)= Zmp + (A –Z)mn – M(A,Z),
получим, что
Q = 3mp + 4mn - ΔW(7Li) + mp – 2(2mp + 2mn – ΔW(4He)) =
= 2·ΔW(4He) - ΔW(7Li) = 2·4· 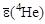 - 7·
- 7· 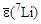 =
=
= 8·7,06 – 7·5,60 = 17,3 МэВ.
Задача 3.6
Получить формулу (3.6).
Решение
Из формулы (3.3) получаем выражение для вычисления энергии реакции:
| Q = T2 –T1 =M1 – M2, | (3.6.1) |
где Т1= Tа + TА и М1 = Mа + МА, Т2 = mb + МB и М2 = mb + МB, – суммарные кинетические энергии и суммарные энергии покоя частиц до и после реакции, которое имеет место в любой инерциальной системе отсчета. Определим порог реакции как минимальное значение кинетической энергии (Та)пор налетающей частицы а (частица А покоится!) в ЛСК, при которой кинетические энергии образовавшихся частиц b и В равна нулю в СЦИ. Для решения задачи удобно воспользоваться релятивистским инвариантом
Е2 – Р2с2 = inv,
который сохраняется для любой изолированной системы в любой инерциальной системе отсчета. Здесь Е = М +Т и Р – полная энергия и импульс произвольной системы тел, взаимодействующих только между собой. Инвариант системы до реакции при пороговой энергии (Та)пор в ЛСК:
inv = [M1+ (Та)пор]2 - 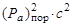 , ,
| (3.6.2) |
но
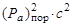 + Mа2 =
+ Mа2 = 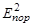 = [Mа + (Та)пор]2,
= [Mа + (Та)пор]2,
откуда
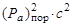 =
= 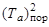 + 2Mа·(Та)пор.
+ 2Mа·(Та)пор.
Подставляя полученное выражение в (3.2) и выполняя необходимые преобразования, получим:
| inv = M12 + 2 Mа2·(Та)пор. | (3.6.3) |
Инвариант для частиц с энергией покоя М2, образовавшихся в результате эндоэнергетической реакции, в СЦИ будет равет:
| inv = M22 , | (3.6.4) |
так как их кинетическая энергия в СЦИ при пороговой кинетической энергии (Та)пор равна нулю.
Приравнивая инварианты (3.6.3) и (3.6.4), получим
(Та)пор= (M22 - M1)2/ 2MАс2=
= (M2 - M12) (M1+ M2) / 2MА=
= (M2 - M1) (M1+ M2 + M1 - M1)/ 2MА =
= (M2 – M1) [2M1+ (M2 - M1)]/2MА =
= 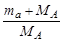 |Q| + |Q| +  , ,
| (3.6.5) |
так как согласно (3.6.1) (M2 – M1) = |Q|. Второе слагаемое в (3.6.5) при |Q| < 100 МэВ ничтожно мало по сравнению с первым, и поэтому
(Та)пор≈ 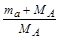 |Q|. |Q|.
| (3.6.6) |
Однако оно становиться значимым при расчете пороговой энергии ядерных реакций, приводящих к рождению барионов и гиперонов.
Решим эту же задачу, используя законы классической (не релятивистской) механики. Законы сохранения энергии и импульса при пороговом значении кинетической энергии налетающей в ЛСК частицы а:
| (Та)пор = |Q|+ Т2; | (3.6.7) |
| Ра = Р2. | (3.6.8) |
Т2 и Р2 определяют движение центра инерции образовавшихся частиц, так как их взаимная кинетическая энергия равна нулю при Та = (Та)пор. Используем классическую связь между импульсом и кинетической энергией
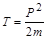 , ,
| (3.6.9) |
так как полагаем, что зависимостью массы системы от скорости можно пренебречь и поэтому скорости движения частиц много меньше скорости света. Действительно, даже если кинетическая энергия (Та)пор налетающей частицы а полностью переходит во внутреннюю энергию и изменяет массу системы, то
ΔМ = М2 – М1 ≤ (Та)пор,
так как (Та)пор << М1, при энергиях налетающих частиц менее 100 МэВ. Поэтому, при кинематических расчетах в нерялитивистском случае можно считать, что
| М2 = М1. | (3.6.10) |
Тогда, из (3.6.1), (3.6.8) и (3.6.9) получаем
(Та)пор = |Q| + 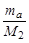 (Та)пор = (Та)пор = 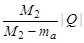 , ,
| (3.6.11) |
или, учитывая (3.6.10),
(Та)пор =  . .
| (3.6.12) |
Полученная формула (3.6.12) является приближенной и ее отличие от точной формулы (3.6.5) вызвано пренебрежением релятивистским изменением массы.
Задача 3.7
Вычислить пороговую кинетическую энергию налетающей частицы в реакции p + 3H → 3He + n, если налетающей частицей является: а) протон; б) ядро трития (тритон).
Решение
По формуле (3.3) рассчитаем энергию реакции
Q = mp + M(3H) - mn – M(3He) = [Δmp + Δ(3H) - Δmn – Δ(3He)]·931,5 =
= [0,007825 + 0,016049 – 0,016030 – 0,0086665]·931,5 = -0,7648 МэВ.
Значения избытков масс атомов взяты из таблицы табл. 1 Приложений. Как видно, реакция эндоэнергетическая.
Пороговая кинетическая энергия согласно формуле (3.6) будет равна:
а) 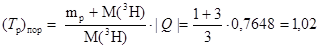 МэВ;
МэВ;
б) 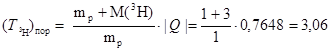 МэВ.
МэВ.
Задача 3.8
Определить кинетическую энергию ядер 7Ве, возникающих в реакции p + 7Li → 7Be + n - 1,65 МэВ при пороговом значении кинетической энергии протона.
Решение
Кинетическая энергия возникающего ядра 7Ве равна
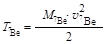 , ,
| (3.8.1) |
где v - скорость движения ядра 7Ве в ЛСК.
Так как скорость относительного движения образовавшихся частиц 7Be и n при пороговой энергии протона равна нулю, то в ЛСК обе образовавшиеся частицы движутся с одинаковой скоростью v2 и
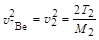 , ,
| (3.8.2) |
где М2 - суммарная масса образовавшихся частиц, а v2 и Т2 –скорость и кинетическая энергия движения центра инерции образовавшихся частиц.
Для нахождения Т2 используем закон сохранения энергии (3.6.7), закон сохранения импульса (3.6.8), формулу (3.6.9) и получаем, что
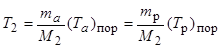 ,
,
или, используя (3.6) (см. задачу 3.6)),
 . .
| (3.8.3) |
Подставив (3.8.3) в (3.8.2), а затем полученное выражение в (3.8.1), получим окончательно
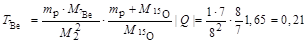 МэВ. МэВ.
|
Задача 3.9
Вычислить энергию реакции 14N(α, p)17O, если энергия налетающих α-частиц Тα = 4 МэВ, а протон, вылетевший под углом 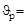 30º к направлению движения α-частицы, имеет энергию Тр = 2,08 МэВ.
30º к направлению движения α-частицы, имеет энергию Тр = 2,08 МэВ.
Решение
 Согласно (3.3) энергия реакции
Согласно (3.3) энергия реакции
Q = T2 – T1 = Tр + 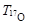 – Tα. – Tα.
| (3.9.1) |
Изобразим графически закон сохранения импульса в виде векторного треугольника (рис. 3.9.1). По теореме косинусов
 . .
| (3.9.2) |
Учитывая, что Р2 = 2mT, из (3.9.2) получим
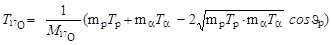 . .
| (3.9.3) |
Подставив это выражение в (3.9.1), имеем
Q = Tр + 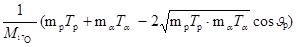 – Tα =
= 2,08 + – Tα =
= 2,08 +  ‑ 4 = -1,2 МэВ. ‑ 4 = -1,2 МэВ.
|
Задача 3.10
Получить в СЦИ формулу (3.5) для импульса 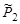 частиц, возникающих в результате ядерной реакции (3.1), если энергия реакции Q, а энергия налетающей частицы а в ЛСК равна Та.
частиц, возникающих в результате ядерной реакции (3.1), если энергия реакции Q, а энергия налетающей частицы а в ЛСК равна Та.
Решение
В случае образования двух новых частиц b и В их импульсы 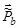 и
и 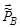 в СЦИ должны быть равны по величине и противоположно направлены:
в СЦИ должны быть равны по величине и противоположно направлены:
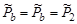 .
.
Из определения энергии реакции (3.3)

| (3.10.1) |
В свою очередь
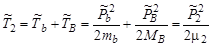 ,
,
где 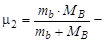 приведенная масса частиц, образовавшихся в результате ядерной реакции.
приведенная масса частиц, образовавшихся в результате ядерной реакции.
Подставив полученное выражение для кинетической энергии 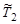 в (3.10.1), получим
в (3.10.1), получим
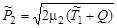 . .
| (3.10.2) |
Выразим суммарную кинетическую энергию 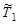 в СЦИ длячастиц, участвующих в ядерной реакции, через кинетическую энергию Та налетающей частицы. Очевидно, что
в СЦИ длячастиц, участвующих в ядерной реакции, через кинетическую энергию Та налетающей частицы. Очевидно, что
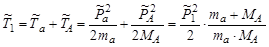 . .
| (3.10.3) |
Но, как следует из рисунка 3.2
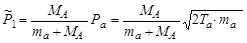 . .
| (3.10.4) |
Подставив (3.10.4) в (3.10.3), получим
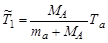 . .
| (3.10.5) |
Используя (3.10.5), формулу (3.10.2) можно записать в более удобном для построения векторных диаграмм виде:
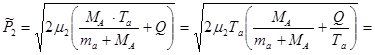 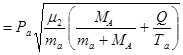 . .
| (3.10.6) |
Задача 3.11
 Определить кинетическую энергию ядер кислорода, вылетающих под углом 30º к направлению бомбардирующих протонов в реакции 14N(p,n)14О, Q = -5,9 МэВ. Кинетическая энергия протонов 10 МэВ. Решение получить с помощью построенной в масштабе векторной диаграммы импульсов для ядерной реакции.
Определить кинетическую энергию ядер кислорода, вылетающих под углом 30º к направлению бомбардирующих протонов в реакции 14N(p,n)14О, Q = -5,9 МэВ. Кинетическая энергия протонов 10 МэВ. Решение получить с помощью построенной в масштабе векторной диаграммы импульсов для ядерной реакции.
Решение
Так как кинетическая энергия вылетающих частиц в СЦИ не зависит от угла вылета, то делаем заключение, что следует определить кинетическую энергию ТО( 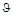 ) в ЛСК. Предварительно напомним, что в нерелятивистском случае, который здесь реализуется (почему?), кинетическая энергия ядер 14О выражается через их импульс обычным образом:
) в ЛСК. Предварительно напомним, что в нерелятивистском случае, который здесь реализуется (почему?), кинетическая энергия ядер 14О выражается через их импульс обычным образом:
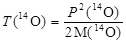 . .
| (3.11.1) |
Для нахождения Р(14О) построим векторную диаграмму импульсов. Для этого определим величину вектора налетающей частицы:
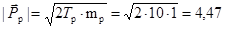 у.е.,
у.е.,
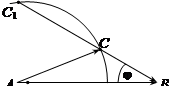
 так как энергию и массу выражаем во внесистемных единицах. Выбираем в качестве масштаба 1 у.е. в 1 см и на рис. 3.11.1 строим направленный отрезок АВ длиной 4,47 см, отображающий вектор импульса налетающего протона. Затем делим этот отрезок точкой «О» на два отрезка АО и ОВ таким образом, чтобы АО : ОВ = mn : M(14O). По формуле (3.5), используя формулу (3.10.5), вычисляем величину импульса образовавшихся частиц в СЦИ.
так как энергию и массу выражаем во внесистемных единицах. Выбираем в качестве масштаба 1 у.е. в 1 см и на рис. 3.11.1 строим направленный отрезок АВ длиной 4,47 см, отображающий вектор импульса налетающего протона. Затем делим этот отрезок точкой «О» на два отрезка АО и ОВ таким образом, чтобы АО : ОВ = mn : M(14O). По формуле (3.5), используя формулу (3.10.5), вычисляем величину импульса образовавшихся частиц в СЦИ.
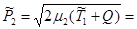
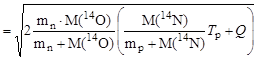 = =
 2,53 у.е. 2,53 у.е.
|
Радиусом R = 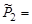 2,53 см проводим дугу с центром в точке «О». Из точки «В» под углом φ = 30º по отношению к отрезку АВ проводим луч до пересечения с дугой в точках «С» и «С1». Направленные отрезки С1В и СВ отображают в ЛСК две возможные величины импульса вылетающих под углом φ = 30º ядер 14О. Соответственно отрезки АС1 и АС отображают в ЛСК две возможные величины импульса образующихся нейтронов. Измерив длину отрезков С1В и СВ получаем, что Р1(14О) = 5,0 у.е., а Р(14О) = 2,2 у.е. Этим величинам импульсов отвечают, согласно формуле (3.11.1), два значения кинетической энергии ядер 14О в ЛСК:
2,53 см проводим дугу с центром в точке «О». Из точки «В» под углом φ = 30º по отношению к отрезку АВ проводим луч до пересечения с дугой в точках «С» и «С1». Направленные отрезки С1В и СВ отображают в ЛСК две возможные величины импульса вылетающих под углом φ = 30º ядер 14О. Соответственно отрезки АС1 и АС отображают в ЛСК две возможные величины импульса образующихся нейтронов. Измерив длину отрезков С1В и СВ получаем, что Р1(14О) = 5,0 у.е., а Р(14О) = 2,2 у.е. Этим величинам импульсов отвечают, согласно формуле (3.11.1), два значения кинетической энергии ядер 14О в ЛСК:
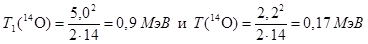 .
.
Полезно получить величины Р1(14О) и Р1(14О) аналитически. Для этого на рис. 3.11.1 соединим точки «О» и «С» и решим треугольник ОВС. Сторона ОС = 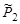 = 2,53 у.е., сторона ОВ =
= 2,53 у.е., сторона ОВ =  = (14/15)Ра = 4,17 у.е. Используя теорему косинусов, получим
= (14/15)Ра = 4,17 у.е. Используя теорему косинусов, получим
ОС2 = СВ2 + ОВ2 – 2СВ·ОВ·соsφ,
или квадратное уравнение для нахождения Р(14О):
2,532 = Р2(14О) + 4,172 - 2Р(14О)· 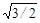 .
.
Это уравнение имеет два корня, которые дают две искомых величины векторов
Р1(14О) = 3,61 + 1,43 = 5,04 у.е.
и
Р2(14О) = 3,61 - 1,43 = 2,18 у.е.,
которые являются, разумеется, более точными, чем значения, полученные выше графическим способом.
Задача 3.12
 Найти максимальную кинетическую энергию α-частиц, возникающих в результате реакции 16O(d, α)14N, Q = +3,1 МэВ при энергии бомбардирующих дейтонов 2,0 МэВ.
Найти максимальную кинетическую энергию α-частиц, возникающих в результате реакции 16O(d, α)14N, Q = +3,1 МэВ при энергии бомбардирующих дейтонов 2,0 МэВ.
Решение
 Для решения задачи воспользуемся векторной диаграммой импульсов (рис. 3.12.1). Кинетическая энергия образующейся α-частицы пропорциональна квадрату ее импульса. В ЛСК длина отрезка АС соответствует импульсу образующейся α-частицы, вылетающей под углом
Для решения задачи воспользуемся векторной диаграммой импульсов (рис. 3.12.1). Кинетическая энергия образующейся α-частицы пропорциональна квадрату ее импульса. В ЛСК длина отрезка АС соответствует импульсу образующейся α-частицы, вылетающей под углом 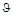 . Поэтому максимальная длина отрезка АС будет соответствует углу
. Поэтому максимальная длина отрезка АС будет соответствует углу 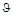 = 0º, т.е. случаю, когда точка «С» совмещается с точкой «С´». Таким образом,
= 0º, т.е. случаю, когда точка «С» совмещается с точкой «С´». Таким образом,

= 2,17Pd .
В последнем выражении при записи 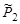 использована формула (3.10.6).
использована формула (3.10.6).
Максимальная энергия α-частицы составит
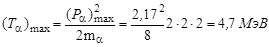
Задача 3.13
Определить ширину энергетического спектра нейтронов, возникающих в реакции 11B(α, n)14N, Q = 0,30 МэВ, если кинетическая энергия бомбардирующих α-частиц равна 5,0 МэВ.
Решение
 Построим векторную диаграмму импульсов (рис. 3.13.1) для реакции 11B(α, n)14N. Импульс образующихся нейтронов (отрезок АС), а, следовательно, и их кинетическая энергия, зависят от угла
Построим векторную диаграмму импульсов (рис. 3.13.1) для реакции 11B(α, n)14N. Импульс образующихся нейтронов (отрезок АС), а, следовательно, и их кинетическая энергия, зависят от угла 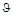 вылета нейтронов. Эти свойства как экзоэнергетических, так и эндоэнергетических реакций с образованием нейтронов используют для получения монохроматических нейтронов, энергию которых можно изменять в диапазоне от (Tn)max до (Tn)max, изменяя угол отбора пучка образующихся нейтронов. Максимальному значению кинетической энергии вылетающих нейтронов соответствует совмещение точки «С» с точкой «С´», а минимальному – совмещение с точкой «С´´». Поэтому
вылета нейтронов. Эти свойства как экзоэнергетических, так и эндоэнергетических реакций с образованием нейтронов используют для получения монохроматических нейтронов, энергию которых можно изменять в диапазоне от (Tn)max до (Tn)max, изменяя угол отбора пучка образующихся нейтронов. Максимальному значению кинетической энергии вылетающих нейтронов соответствует совмещение точки «С» с точкой «С´», а минимальному – совмещение с точкой «С´´». Поэтому

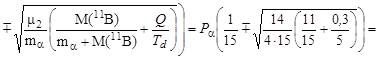
= {0,36·Pα, 0,50·Pα}.
Учитывая, что
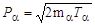 ,
,
получим окончательно:
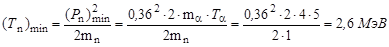 ;
;
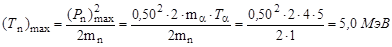
 Задача 3.14
Задача 3.14
Найти максимально возможные углы вылета (в ЛСК) продуктов реакции 9Be(p,n)9B, Q = -1,84 МэВ, если Тр = 4,00 МэВ.

Решение
Проще и нагляднее получить решение, используя векторную диаграмму импульсов (рис. 3.14.1). Так как точка «С» перемещается по дуге окружности от точки «С´» до точки «С´´», то максимальное значение угла вылета нейтрона 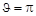 . Однако максимальная величина угла
. Однако максимальная величина угла 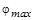 вылета ядра 9В определяется положением касательной СВ к окружности. Из прямоугольного треугольника ОСВ
вылета ядра 9В определяется положением касательной СВ к окружности. Из прямоугольного треугольника ОСВ
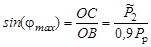 .
.
Численное значение угла φmax предлагается получить самостоятельно.
Задача 3.15
Найти пороговую энергию γ-квантов, при которой становится возможной эндоэнергетическая реакция фоторасщепления покоящегося ядра массой М1, если энергия реакции равна Q.
Решение
Запишем закон сохранения энергии и импульса для данной реакции при пороговом значении энергии (Еγ)пор налетающего γ-кванта:
(Еγ)пор + М1с2 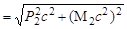 ; ;
| (3.15.1) |
| Р1 = Р2, | (3.15.2) |
где Р1 и Р2 – суммарные величины импульсов до и после взаимодействия в ЛСК, а М2 – суммарная масса покоя образовавшихся частиц. Так как Р1 = (Еγ)пор/с (ядро М1 покоится!), то из (3.15.1) и (3.15.2) получаем
(Еγ)пор + М1с2 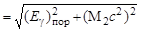 . .
| (3.15.3) |
Возведя левую и правую части (3.15.3) в квадрат, после несложных преобразований получим
(Еγ)пор = 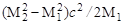 . .
| (3.15.4) |
По определению
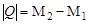 .
.
Поэтому (3.15.4) приводится к виду
(Еγ)пор = 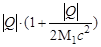 . .
| (3.15.5) |
Так как  , то вторым слагаемым в скобках выражения (3.15.5) часто пренебрегают.
, то вторым слагаемым в скобках выражения (3.15.5) часто пренебрегают.
Задача 3.16.
Найти возможное значение спина основного состояния ядра 17О, возникающего в реакции срыва при взаимодействии дейтронов с ядрами 16О, если известно, что орбитальный момент захватываемых нейронов ln = 2. Сравнить результат со значением спина по оболочечной модели ядра.
Решение
Предполагается, что в реакции срыва электрическое поле ядра ориентирует дейтон таким образом, что в момент наибольшего сближения ядра и дейтона, ближним к ядру оказывается нейтрон, который и захватывается ядром, а протон продолжает движение. Ядро 16О является дважды магическим ядром, у которого заполнены как протонные, так и нейтронные 1s и 1р оболочки. Поэтому спин ядра 16О равен нулю. Захват нейтрона с образованием основного состояния ядра 17О может произойти, согласно оболочечной модели, только на нижний уровень 1d5/2, спин которого равен 5/2.
Согласно правилу сложения квантово-механических векторов, возможные значения спина ядра 17О могут принимать следующие значения:
I(17O) = I(16O) + ln + sn = 0 + 2 ±1/2 = 5/2 и 3/2.
Второе значение спина отвечает возбужденному уровню 1d3/2 ядра 17О, переход с которого в основное состояние должен сопровождаться испусканием магнитного дипольного γ-кванта M1 (рис.1.1).
Дата добавления: 2016-06-13; просмотров: 2959;
