Взаимодействие нейтронов с ядрами
Формула Брейта-Вигнера для изолированного уровня – сечение образования составного ядра при захвате нейтрона с l = 0:
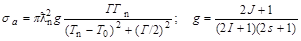 . .
| (4.1) |
Нейтронов с энергией меньше 10 кэВ, а именно в этом энергетическом диапазоне расположены, в основном, резонансы, имеют де-бройлевскую длину волны  > 4,5·10-12 см (см. формулу 4.5), которая существенно превышает размер даже самых тяжелых ядер. Поэтому такие нейтроны могут взаимодействовать с ядрами только с орбитальным моментом l = 0 и в этом случае им не нужно преодолевать центробежный барьер.
> 4,5·10-12 см (см. формулу 4.5), которая существенно превышает размер даже самых тяжелых ядер. Поэтому такие нейтроны могут взаимодействовать с ядрами только с орбитальным моментом l = 0 и в этом случае им не нужно преодолевать центробежный барьер.
 В формуле (4.1):
В формуле (4.1): 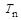 - кинетическая энергия налетающего нейтрона; Т0 – кинетическая энергия нейтрона, соответствующая образованию рассматриваемого уровня составного ядра; g - статистический фактор; I - спин ядра мишени; J - спин рассматриваемого уровня составного ядра; s = 1/2 – спин нейтрона; Г и Гn – полная и нейтронная ширина уровня (см. задачу 4.6).
- кинетическая энергия налетающего нейтрона; Т0 – кинетическая энергия нейтрона, соответствующая образованию рассматриваемого уровня составного ядра; g - статистический фактор; I - спин ядра мишени; J - спин рассматриваемого уровня составного ядра; s = 1/2 – спин нейтрона; Г и Гn – полная и нейтронная ширина уровня (см. задачу 4.6).
Нейтронная ширина уровня
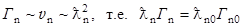 , ,
| (4.2) |
где 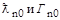 - длина волны нейтрона и нейтронная ширина уровня при Тn = Т0.
- длина волны нейтрона и нейтронная ширина уровня при Тn = Т0.
Основные параметры резонансов представлены на рис. 4.1. Г1 и Г2 – ширины резонансной кривой на половине высоты соответствующего максимума. Остальные обозначения очевидны.
Уровень называется изолированным (уединенным), если
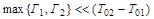 . .
| (4.4) |
Де-бройлевская длина волны нейтрона
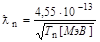 , см. , см.
| (4.5) |
Центробежный барьер для нейтрона
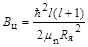 , ,
| (4.6) |
где 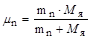 - приведенная масса ядра и нейтрона.
- приведенная масса ядра и нейтрона.
Задача 4.1
Получить с помощью квазиклассических рассуждений выражение для прицельного параметра b бомбардирующего нейтрона. Вычислить первые три возможных значения b для нейтронов с кинетической энергией Tn = 1,00 МэВ.
Решение
 Величина момента импульса
Величина момента импульса 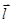 частицы (орбитального момента) относительно произвольной точки «О»
частицы (орбитального момента) относительно произвольной точки «О»
 ,
,
где b – прицельный параметр; Р – величина импульса. В квантовой механике величина 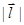 может принимать значения:
может принимать значения:
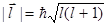 ,
,
где l = 0, 1, 2, . . . – квантовое число момента. Из двух последних соотношений получаем возможные значения
 . .
| (4.1.1) |
Вычислим по формуле (4.5) длину волны де-Бройля для нейтрона с кинетической энергией Tn = 1,00 МэВ:
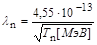 = 4,55·10-13 см. = 4,55·10-13 см.
| (4.1.2) |
Соответственно первые три значения прицельного параметра равны: 0; 6,4 и 11,2 Фм.
Задача 4.2
Найти максимальное значение bmax прицельного параметра при взаимодействии нейтрона с кинетической энергией Tn = 5,00 МэВ с ядрами Ag.
Решение
Будем считать, что ядро имеет сферическую форму, а максимальное значение bmax прицельного параметра нейтрона не должно превышать величины  , которая определяет зону действия ядерных сил между нейтроном и ядром. Тогда, используя 4.1.1, имеем
, которая определяет зону действия ядерных сил между нейтроном и ядром. Тогда, используя 4.1.1, имеем
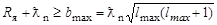 . .
| 4.2.1 |
Из выражения 4.2.1 для известных величин 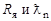 определяется lmax, а затем по формуле 4.1.1 находим bmax.
определяется lmax, а затем по формуле 4.1.1 находим bmax.
Вычисления для радиуса ядра по формуле (1.1) дают Rя = 6,7·10-13 см, а для длины волны нейтрона с энергией Tn = 5,00 МэВ по формуле (4.5) получаем 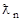 = 2,0·10-13 см. Таким образом, lmax = 3 и, согласно формуле (4.1.1), bmax = 7·10-13 см.
= 2,0·10-13 см. Таким образом, lmax = 3 и, согласно формуле (4.1.1), bmax = 7·10-13 см.
Задача 4.3
Показать, что для нейтронов с длиной волны 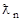 геометрическое сечение взаимодействия с ядром
геометрическое сечение взаимодействия с ядром  , где R – радиус ядра. Оценить эту величину для нейтронов с энергией Tn = 10 МэВ, налетающих на ядро Au.
, где R – радиус ядра. Оценить эту величину для нейтронов с энергией Tn = 10 МэВ, налетающих на ядро Au.
Решение
Для того чтобы нейтрон попал в зону действия ядерных сил, его прицельный параметр не должен превышать величины  . Поэтому проводя из центра ядра окружность радиуса R =
. Поэтому проводя из центра ядра окружность радиуса R =  , получим оценку геометрического сечения взаимодействия нейтрона с ядром
, получим оценку геометрического сечения взаимодействия нейтрона с ядром  . Для золота и нейтрона с кинетической энергией Tn = 10 МэВ (используя формулы (1.1) и (4.5), получим
. Для золота и нейтрона с кинетической энергией Tn = 10 МэВ (используя формулы (1.1) и (4.5), получим
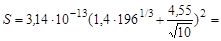 2,9·10-24 см2 = 2,9 барн.
2,9·10-24 см2 = 2,9 барн.
Задача 4.4
Оценить максимальную величину центробежного барьера для нейтронов с кинетической энергией Tn = 7,0 МэВ при взаимодействии с ядрами Sn.
Решение
Для решения задачи воспользуемся формулой (4.6)
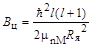 . .
| 4.4.1 |
Приведенная масса системы нейтрон – ядро Sn составляет
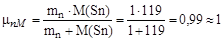 а.е.м. а.е.м.
| 4.4.2 |
Радиус ядра (см. формулу (1,1))
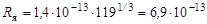 см.
см.
Длину волны нейтрона определим по формуле (4.5)
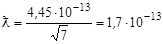 см.
см.
Максимальную величину орбитального момента нейтрона оценим, используя формулу 4.2.1:
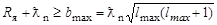 ,
,
подставив в которую значения  , получим lmax = 3.
, получим lmax = 3.
Искомая высота центробежного барьера
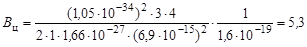 МэВ.
МэВ.
Задача 4.5
Найти вероятность того, что в результате взаимодействия медленных нейтронов (l = 0) с ядрами, спин которых I = 1, составное ядро образуется в основном состоянии со спином J = 3/2. Считать, что спины нейтронов и ядер до взаимодействия имеют всевозможные взаимные ориентации.
Решение
Связанное состояние, которым является составное ядро, имеет вектор спина 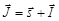 , где
, где 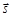 – вектор спина нейтрона. Сложение векторов
– вектор спина нейтрона. Сложение векторов  есть сложение их проекций на выбранное направление в пространстве как алгебраических чисел. Каждый из векторов
есть сложение их проекций на выбранное направление в пространстве как алгебраических чисел. Каждый из векторов  имеет по (2s + 1) или (2I +1) проекций соответственно. Для получения всех возможных проекций вектора
имеет по (2s + 1) или (2I +1) проекций соответственно. Для получения всех возможных проекций вектора  , каждая из возможных проекций вектора
, каждая из возможных проекций вектора 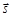 складывается с одной из проекций вектора
складывается с одной из проекций вектора  . Всего таких суммарных проекций оказывается (2s + 1)(2I +1), каждая из которых реализуется с равной вероятностью. Таким образом, возможны (2s + 1)(2I +1) различных способов образования составного ядра. Число же возможных и равновероятных проекций вектора
. Всего таких суммарных проекций оказывается (2s + 1)(2I +1), каждая из которых реализуется с равной вероятностью. Таким образом, возможны (2s + 1)(2I +1) различных способов образования составного ядра. Число же возможных и равновероятных проекций вектора 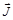 составляет (2J +1), а относительная вероятность образования составного ядра со спином J составит (ср. с формулой (4.1))
составляет (2J +1), а относительная вероятность образования составного ядра со спином J составит (ср. с формулой (4.1))
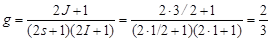 .
.
Задача 4.6
Исходя из формулы Брейта-Вигнера для сечения σа образования составного ядра, получить выражение для сечений процессов упругого рассеяния σnn и радиационного захвата σnγ нейтрона.
Решение
Вероятность распада (постоянная распада) составного ядра в единицу времени с одного из рассматриваемых изолированных (уединенных) уровней
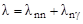 , ,
| 4.6.1 |
где 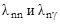 - вероятности распада составного ядра по каналам (n,n) и (n,γ) соответственно, если других каналов распада составного ядра нет. Учитывая связь между постоянной распада λ и средним временем τ жизни ядра, из 4.6.1 получим
- вероятности распада составного ядра по каналам (n,n) и (n,γ) соответственно, если других каналов распада составного ядра нет. Учитывая связь между постоянной распада λ и средним временем τ жизни ядра, из 4.6.1 получим
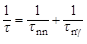 . .
| 4.6.2 |
Из соотношения неопределенностей 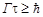 и 4.6.2, предполагая, что измерения производятся с наилучшей точностью, получим
и 4.6.2, предполагая, что измерения производятся с наилучшей точностью, получим
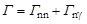 , ,
| (4.6.3) |
т.е. полная ширина есть сумма парциальных ширин. Таким образом, относительные вероятности распада составного ядра по каналам (n,n) и (n,γ) будут равны соответственно
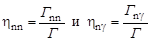 , ,
| (4.6.4) |
а соответствующие сечения
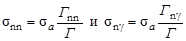 , ,
| (4.6.5) |
Задача 4.7
Выразить с помощью формулы Брейта-Вигнера сечение радиационного захвата нейтрона σnγ от его кинетической энергии Tn, если известно сечение σ0 данного процесса при Tn = Т0 и значения Т0 и Г.
Решение
Из формул (4.1) и (4.6.5) получаем формулу Брейта-Вигнера для сечения радиационного захвата
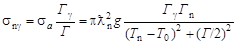 . .
| (4.7.1) |
Тогда
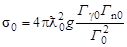 . .
| (4.7.2) |
Разделив (4.7.1) на (4.7.2), получим
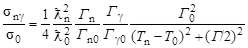 . .
| (4.7.3) |
Так как формула (4.1) Брейта-Вигнера записана для l = 0 (Tn < 10 кэВ), то можно положить Гγ ≈ const, так как энергия возбуждения составного ядра
ΔW(C) = 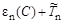 ,
,
а энергия связи нейтрона 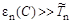 . Кроме того, испускание γ-кванта в этой области энергий налетающих нейтронов является преобладающим процессом распада составного ядра, так выброс нейтрона сильно затруднен из-за очень малого превышения энергии возбуждения составного ядра над энергией связи нейтрона. Поэтому Гγ >>Гn и полная ширина уровня Г = Гγ + Гn ≈ Гγ ≈ const. С учетом этого и формулы (4.2) из (4.7.3) получим
. Кроме того, испускание γ-кванта в этой области энергий налетающих нейтронов является преобладающим процессом распада составного ядра, так выброс нейтрона сильно затруднен из-за очень малого превышения энергии возбуждения составного ядра над энергией связи нейтрона. Поэтому Гγ >>Гn и полная ширина уровня Г = Гγ + Гn ≈ Гγ ≈ const. С учетом этого и формулы (4.2) из (4.7.3) получим
 ,
,
так как
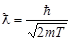 .
.
Задача 4.8
Выяснить с помощью формулы Брейта-Вигнера условия, при которых сечение радиационного захвата нейтронов подчиняется закону 1/v (см. пунктир на рис. 4.1)
Решение
Исследуем формулу (4.7.1) Брейта-Вигнера для сечения радиационного захвата, сделав следующие три предположения:
1. Тn << Т0;
2. Гγ ≈ const;
3. Гγ >>Гn и полная ширина уровня Г = Гγ + Гn ≈ Гγ ≈ const.
Возможность применения последних двух предположений обсуждены в предыдущей задаче.
Тогда
 ,
,
т.е.
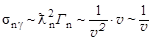 .
.
Задача 4.9
Найти с помощью формулы (4.7.1) Брейта-Вигнера для сечения радиационного захвата нейтрона отношение σmin/σ0, где σmin – минимальное сечение процесса (n,γ) в области Tn < T0 (см. рис. 4.1); σ0 – сечение этого процесса при Tn = T0, если Г << Т0.
Решение
Считая Гγ ≈ const и Г ≈ const, из формулы (4.7.1) для сечения процесса радиационного захвата нейтрона получим
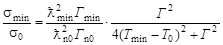 . .
| (4.9.1) |
Для нахождения Tmin продифферинцируем формулу (4.7.1) по Tn и результат приравняем нулю. После несложных преобразований получим квадратное уравнение
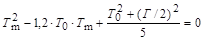 .
.
Из этого уравнения
 ,
,
так как Г << Т0. Подставив полученное значение Tmin в (4.9.1), получим
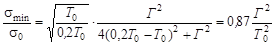 .
.
Задача 4.10
Какова должна быть толщина d кадмиевой пластинки, чтобы параллельный пучок тепловых нейтронов при похождении через нее уменьшился в 100 раз?
Решение
 Пусть плотность потока параллельного пучка нейтронов, падающих на пластинку, есть Ф0. По мере прохождения пластинки, плотность потока нейтронов будет уменьшаться вследствие захвата их ядрами кадмия. Выделим в пластинке на глубине х слой толщиной dx. Изменение плотности потока при прохождении слоя dx равно
Пусть плотность потока параллельного пучка нейтронов, падающих на пластинку, есть Ф0. По мере прохождения пластинки, плотность потока нейтронов будет уменьшаться вследствие захвата их ядрами кадмия. Выделим в пластинке на глубине х слой толщиной dx. Изменение плотности потока при прохождении слоя dx равно

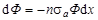 ,
,
где n – концентрация ядер поглотителя нейтронов; σа – сечение поглощения тепловых нейтронов.
Решение этого уравнения с граничным условием Ф(х = 0) = Ф0 имеет вид
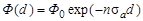 , ,
| (4.10.1) |
где d – толщина пластинки. Из (4.10.1) получим
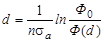 . .
| (4.10.2) |
Тепловые нейтроны эффективно захватываются только ядрами 113Cd, атомное содержание которого в природном кадмии составляет 12,26%. Сечение захвата тепловых нейтронов σа(113Cd) = 2·104 б. Для вычисления d найдем концентрацию ядер 113Cd:
 .
.
Окончательно,
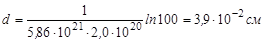 .
.
Задача 4.11
 В центре сферического слоя графита, внутренний и внешний радиусы которого R1 = 1,0 см и R2 = 10,0 см находится точечный источник нейтронов с кинетической энергией Тn = 2 МэВ. Интенсивность источника I0 =2,0·104 с-1. Сечение взаимодействия нейтронов данной энергии с ядрами углерода σ = 1,6 б. Определить плотность потока нейтронов Фn(R2) на внешней поверхности графита, проходящих данный слой без столкновений.
В центре сферического слоя графита, внутренний и внешний радиусы которого R1 = 1,0 см и R2 = 10,0 см находится точечный источник нейтронов с кинетической энергией Тn = 2 МэВ. Интенсивность источника I0 =2,0·104 с-1. Сечение взаимодействия нейтронов данной энергии с ядрами углерода σ = 1,6 б. Определить плотность потока нейтронов Фn(R2) на внешней поверхности графита, проходящих данный слой без столкновений.
Решение
 Приступая к решению этой задачи, рекомендуется хорошо разобрать решение задачи 3.22. Построим элемент телесного угол dΩ с вершиной в точке нахождения источника (рис. 4.11.1). По определению, плотность потока нейтронов в точке R2 будет равна
Приступая к решению этой задачи, рекомендуется хорошо разобрать решение задачи 3.22. Построим элемент телесного угол dΩ с вершиной в точке нахождения источника (рис. 4.11.1). По определению, плотность потока нейтронов в точке R2 будет равна
 . .
| (4.11.1) |
где 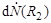 – количество нейтронов, падающих со стороны графита на площадку dS в секунду, не испытавших рассеяния. Количество нейтронов, испущенных источником в телесный угол dΩ в одну секунду и падающих на внутреннюю поверхность слоя в точке R1, составит
– количество нейтронов, падающих со стороны графита на площадку dS в секунду, не испытавших рассеяния. Количество нейтронов, испущенных источником в телесный угол dΩ в одну секунду и падающих на внутреннюю поверхность слоя в точке R1, составит
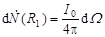 .
.
Так как часть нейтронов испытает рассеяние на ядрах углерода, то в соответствие с формулой (4.10.1), число нейтронов, не испытавших рассеяния и проходящих в секунду через площадку dS в точке R2 составит
 ,
,
где n – концентрация ядер углерода.
Подставив полученное выражение в (4.11.1) и воспользовавшись определением (3.22.2) для элемента телесного угла, получим
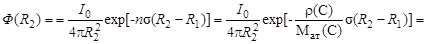
 .
.
Задача 4.12
Узкий пучок нейтронов с кинетической энергией 10 эВ проходит через счетчик длиной l = 15 см вдоль его оси. Счетчик наполнен газообразным BF3 при нормальных условиях (бор природного изотопного состава). Определить эффективность регистрации нейтронов с данной энергией, если известно, что сечение реакции (n,α) подчиняется закону 1/v.
Решение
Эффективность ε регистрации частиц – одна из основных характеристик любого счетчика частиц, которая есть вероятность зарегистрировать ровно N частиц из N0 вошедших в рабочий объем счетчика за время измерения. Для экспериментальной оценки величины ε используют соотношение
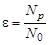 , ,
| (4.12.1) |
где Np – число зарегистрированных частиц, а N0– число частиц, попавших в рабочий объем детектора за время регистрации.
Непосредственная регистрация нейтронов данной энергии невозможна из-за крайне низкой кинетической энергии. Для регистрации используют экзоэнергетические реакции под действием нейтронов с образованием заряженных частиц, которые регистрируются обычными ионизационными методами. Одна из таких реакций
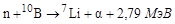 , ,
| (4.12.2) |
протекает только на нуклиде 10В. Сечение этой реакции в тепловой области (Тn = 0,025 эВ) σ = 3813 б.
В соответствие с формулой (4.10.1) плотность потока нейтронов на выходе из детектора составит
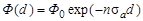 ,
,
а поглощенная в счетчике длиной d плотность потока
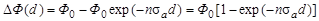 , ,
| (4.12.3) |
где Ф0 – плотность потока нейтронов, входящих в счетчик через торцевую поверхность.
Если каждая α-частица, возникающая в реакции (4.12.2) оказывается зарегистрированной, то, согласно (4.12.1) и (4.12.3)
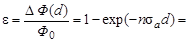
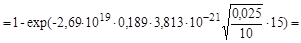 1,44·10-2,
1,44·10-2,
так как при нормальных условиях в 1 см3 идеального газа содержится L = 2,69·1019 молекул (число Лошмидта).
Задача 4.13
 Небольшой образец ванадия 51V массой m = 0,5 г активируется до насыщения в поле тепловых нейтронов. Непосредственно после облучения в течение t = 5,0 мин было зарегистрировано
Небольшой образец ванадия 51V массой m = 0,5 г активируется до насыщения в поле тепловых нейтронов. Непосредственно после облучения в течение t = 5,0 мин было зарегистрировано 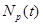 = 8,0·109 импульсов при эффективности регистрации ε = 1,0·10-2. Определить концентрацию nn нейтронов, падающих на образец.
= 8,0·109 импульсов при эффективности регистрации ε = 1,0·10-2. Определить концентрацию nn нейтронов, падающих на образец.
Решение
В результате захвата тепловых нейтронов ядрами 51V образуется радиоактивный 52V (сечение активации σакт= 4,5 б), который испускает β--частицы и с периодом полураспада Т1/2 = 3,26 мин превращается в стабильный нуклид 52Cr.
Плотность потока нейтронов Фn может быть выражена через концентрацию нейтронов nn и их среднюю скорость 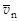 следующим образом:
следующим образом:
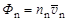 . .
| (4.13.1) |
Число импульсов, зарегистрированных за время t,
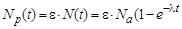 ),
),
где N(t) – число ядер, испытавших за время t β--распад, а Na– число радиоактивных ядер при насыщении. Если воспользоваться формулой (2.3), то
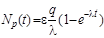 . .
| (4.13.2) |
Здесь q - скорость образования радиоактивных ядер 52V, распад которых регистрируется.
По определению, число реакций в бесконечно малом объеме вещества мишени в единицу времени составляет
 ,
,
где n – концентрация ядер мишени; σакт- сечение активации; Фn – плотность потока нейтронов. Тогда скорость образования радиоактивных ядер в бесконечно малом объеме вещества мишени составит
 .
.
Чтобы найти скорость q образования радиоактивных ядер во всем образце следует полученное выражение проинтегрировать по объему
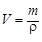 ,
,
который занимает вещество данной массы m и плотностью ρ:

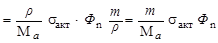 , ,
| (4.13.3) |
если считать, что плотность потока нейтронов и сечение активации в пределах объема образца не изменяются (образец «тонкий»).
Покажем, что такое допущение имеет место. Длина пробега нейтронов до первого взаимодействия
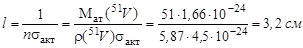 ,
,
что на много превышает характерные линейные размеры образца:
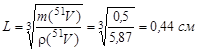 .
.
Окончательно из (4.13.1), (4.13.2) и (4.13.3) получим
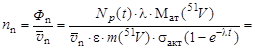

= 7,4·104 см-3.
Задача 4.14
Какую долю η первоначальной кинетической энергии Т0 теряет нейтрон при: а) упругом лобовом столкновении с первоначально покоившимися ядрами 2Н, 12С и 235U; б) упругом рассеянии под углом  на первоначально покоившемся дейтоне, если угол
на первоначально покоившемся дейтоне, если угол  = 30, 90 и 150º?
= 30, 90 и 150º?
Решение
Доля энергии, теряемая нейтроном,
 , ,
| (4.14.1) |
где 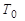 и Р0 - кинетическая энергия и импульс налетающего нейтрона;
и Р0 - кинетическая энергия и импульс налетающего нейтрона; 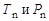 - кинетическая энергия и импульс нейтрона после рассеяния.
- кинетическая энергия и импульс нейтрона после рассеяния.
Решение задачи получим в ЛСК. Запишем закон сохранения энергии и импульса:
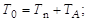
| (4.14.2) |
 , ,
| (4.14.3) |

|
 - импульс налетающего нейтрона;
- импульс налетающего нейтрона; 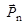 - импульс нейтрона после рассеяния;
- импульс нейтрона после рассеяния;  - кинетическая энергия и импульс ядра отдачи с массовым числом А. Из векторного треугольника (рис. 4.14.1), графически изображающего закон сохранения импульса (4.14.3), имеем
- кинетическая энергия и импульс ядра отдачи с массовым числом А. Из векторного треугольника (рис. 4.14.1), графически изображающего закон сохранения импульса (4.14.3), имеем
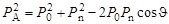 . .
| (4.14.4) |
Из (4.14.2), учитывая, что Т = P2/2m, получим
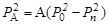 . .
| (4.14.5) |
Подставив (4.14.5) в (4.14.4), после несложных преобразований, получим квадратное уравнение
 .
.
Решение этого уравнения:
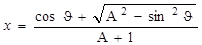 .
.
Окончательно
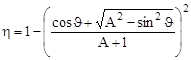 . .
| (4.14.6) |
а) При лобовом столкновении с телом большей массы нейтрон отлетает назад и выражение (4.14.6) приобретает вид
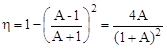 . .
| (4.14.7) |
Для А = 2 (2Н), 12 (12С) и 238 (238U) получим соответственно
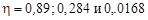 .
.
б) При столкновении нейтрона с ядром 2H (А = 2) выражение (4.14.6) приобретает вид:
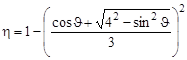 . .
| (4.14.8) |
Для углов  = 30, 90 и 150º получим соответственно
= 30, 90 и 150º получим соответственно
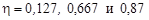 .
.
Задача 4.15
Нейтроны с кинетической энергией Т0 упруго рассеиваются на ядрах с массовым числом А. Определить: а) энергию Т нейтронов рассеянных под углом 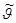 в СЦИ; б) долю нейтронов, кинетическая энергия которых в результате однократного рассеяния лежит в интервале (Т, Т + dТ), если рассеяние в СЦИ изотропно.
в СЦИ; б) долю нейтронов, кинетическая энергия которых в результате однократного рассеяния лежит в интервале (Т, Т + dТ), если рассеяние в СЦИ изотропно.
Решение
а) Запишем закон сохранения энергии:
Т0 = Т + ТА,
где ТА – кинетическая энергия ядра отдачи с массовым числом А.
Тогда
| Т = Т0 - ТА. | (4.15.1) |
 Для нахождения ТА воспользуемся векторной диаграммой импульсов(рис. 4.15.1). По теореме косинусов
Для нахождения ТА воспользуемся векторной диаграммой импульсов(рис. 4.15.1). По теореме косинусов
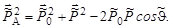
Но при упругом рассеянии величина импульса частиц в СЦИ не изменяется и по правилам построения импульсной диаграммы для упругого рассеяния
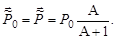
Тогда
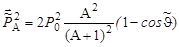
 и
и
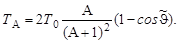
Подставив полученное выражение для ТА в (4.15.1), получим окончательно:
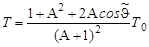 . .
| (4.15.2) |
б)Если рассеяние нейтронов в СЦИ изотропно, то число нейтронов 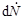 , рассеянных в единичный телесный угол
, рассеянных в единичный телесный угол 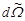 в единицу времени, составит
в единицу времени, составит
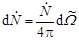 ,
,
где 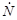 - полное число нейтронов, испытавших рассеяние по всем возможным направлениям. Доля нейтронов
- полное число нейтронов, испытавших рассеяние по всем возможным направлениям. Доля нейтронов 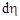 , рассеянных в единицу времени в элемент телесного угла
, рассеянных в единицу времени в элемент телесного угла 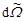 ,
,
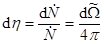 .
.
В сферической системе координат с центром в точке рассеяния
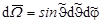
и
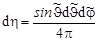 .
.
Так как рассеяние нейтронов в СЦИ по условия задачи сферически симметрично, то угол 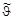 не зависит от полярного угла
не зависит от полярного угла 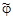 и
и
 . .
| (4.15.3) |
Связь между кинетической энергией рассеянного нейтрона и углом рассеяния 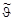 в СЦИ дается формулой (4.15.2). Дифференцируя формулу (4.15.2), получим
в СЦИ дается формулой (4.15.2). Дифференцируя формулу (4.15.2), получим
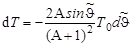 .
.
Выразив из последнего выражения 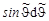 и подставив в (4.15.3), получим окончательно, что
и подставив в (4.15.3), получим окончательно, что
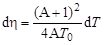 , ,
| (4.15.4) |
а функция распределения рассеянных нейтронов по энергиям (энергетический спектр)
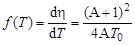 .
.
 Таким образом, вероятность нейтрону иметь энергию от Тminдо Тmax оказывается одинаковой. Минимальному значению энергии рассеянного нейтрона соответствует рассеяние назад (
Таким образом, вероятность нейтрону иметь энергию от Тminдо Тmax оказывается одинаковой. Минимальному значению энергии рассеянного нейтрона соответствует рассеяние назад ( 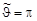 ). Тогда из формулы (4.15.2) получаем
). Тогда из формулы (4.15.2) получаем
 .
.
Максимальному значению энергии нейтрона в энергетическом спектре соответствует отсутствие взаимодействия с ядрами мишени, т.е. Тmax= Т0. Этот же результат следует из формулы (4.15.2) при  .
.
Энергетический спектр рассеянных нейтронов изображен на рис. 4.15.2.
Задача 4.16
Нейтроны испытывают рассеяние на первоначально покоившихся протонах. Считая это рассеяние изотропным в СЦИ, найти с помощью векторной диаграммы импульсов:
а) вероятность рассеяния нейтронов в интервале углов  ;
;
б) долю нейтронов, рассеянных под углами 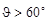 ;
;
в) среднее значение угла рассеяния нейтронов в ЛСК.
Решение
 Построим векторную диаграмму импульсов (рис. 4.16.1), не делая различия между массами протона и нейтрона.
Построим векторную диаграмму импульсов (рис. 4.16.1), не делая различия между массами протона и нейтрона.
а) В качестве оценки вероятности рассеяния нейтронов в интервале углов 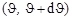 можно использовать (4.15.3), если установить функциональную связь между углами
можно использовать (4.15.3), если установить функциональную связь между углами 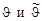 . Из векторной диаграммы
. Из векторной диаграммы
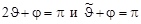 .
.
Следовательно
 . .
| (4.16.1) |
Тогда из (4.15.3) и (4.16.1)
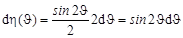 . .
| (4.16.2) |
б)Доля нейтронов, рассеянных под углами 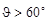 , составит
, составит
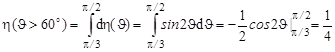 ,
,
так как максимально возможный угол рассеяния нейтрона в данном случае составляет 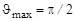 .
.
в) Среднее значение угла рассеяния нейтрона найдем обычным образом:
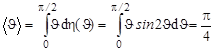 .
.
Дата добавления: 2016-06-13; просмотров: 5761;