Задачи для самостоятельного решения. Оценить плотность ядерного вещества ρ, концентрацию нуклонов n и плотность электрического заряда ρэ в ядре.
Задача 1.1
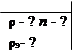 Оценить плотность ядерного вещества ρ, концентрацию нуклонов n и плотность электрического заряда ρэ в ядре.
Оценить плотность ядерного вещества ρ, концентрацию нуклонов n и плотность электрического заряда ρэ в ядре.
Решение
По определению, плотность вещества массой М, которое занимает объем V, равна
| ρ = М/V = m·N/V, | (1.1.1) |
где m – масса частиц, из которых состоит тело (предполагаем, что частицы тождественны), а N – количество частиц в объеме V. Так как
| n = N/V | (1.1.2) |
есть концентрация частиц по определению, то из (1.1) и (1.2)
| ρ = m· n. | (1.1.3) |
Для оценки примем, что ядро, состоящее из А нуклонов, имеет форму шара, радиус которого R(A) дается формулой (1.1). Тогда
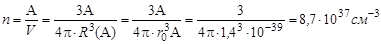 , ,
|
Будем считать, что масса нуклона равна одной атомной единице массы, т.е. m = 1,66·10-24 г,и окончательно получим
ρ = 1,66·10-24·8,7·1037 = 1,4·1014 г/см-3= 1,4·108 тонн/см-3!
Плотность электрического заряда в ядре равна
| ρэ = e·np, | (1.1.4) |
где np- концентрация протонов в ядре. Если считать, что для устойчивых ядер число протонов в ядре равно числу нейтронов, то
| ρэ = e·n/2= 1,6·10-19·8,7·1037= 7·1018 Кл/см-3 . |
Задача 1.2
В современной системе масс атомов за единицу массы а.е.м. принята 1/12 массы атома 12С (вместо старой единицы МЕ, равной 1/16
массы атома 16О). Найти связь между а.е.м. и МЕ. Как изменились численные значения масс атомов при переходе от старой единицы массы к новой.
Решение
Задачу удобно решать, используя избытки масс нуклидов:
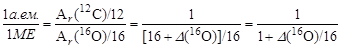
| 1.2.1 |
так как по определению избыток масс атома 12С равен нулю. Подставив в (1.2.1) численное значение Δ(16О) их таблицы табл. 1 Приложений, получим
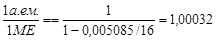
|
Таким образом, 1 а.е.м. численно стала больше 1 МЕ на 0,032 %, а численные значения масс атомов уменьшились на эту же величину.
Задача 1.3
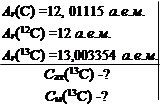 Найти относительное содержание Сат и См (атомное и массовое) нуклида13С в природном углероде, который состоит из нуклидов 12С и 13С. Атомные массы природного углерода и обоих нуклидов считать известными.
Найти относительное содержание Сат и См (атомное и массовое) нуклида13С в природном углероде, который состоит из нуклидов 12С и 13С. Атомные массы природного углерода и обоих нуклидов считать известными.
Решение
Из периодической системы химических элементов находим, что Ar(C) =12, 01115 а.е.м. Из табл. 1 Приложений находим, что избыток массы Δ(13С) = 0,003354 а.е.м. и Ar(13C) =13, 003354 а.е.м. По определению относительное атомное содержание изотопа Сат есть доля атомов этого изотопа в полном числе атомов моля элемента природного изотопного состава. Тогда по определению
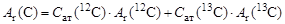 . .
| (1.3.1) |
Учитывая, что
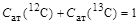 , ,
|
перепишем (1.3.1) в виде
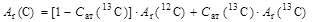 , ,
|
и решим относительно Сат(13C):
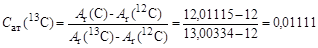 . .
|
Учитывая, что массовое содержание изотопа См есть доля массы этого изотопа в моле элемента природного изотопного состава, сразу получаем
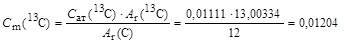 . .
|
Задача 1.4
 Найти с помощью формулы (1.3) энергию связи ядра, которое имеет одинаковое число протонов и нейтронов, а радиус – в полтора раза меньший, чем радиус ядра 27Al.
Найти с помощью формулы (1.3) энергию связи ядра, которое имеет одинаковое число протонов и нейтронов, а радиус – в полтора раза меньший, чем радиус ядра 27Al.
Решение
Чтобы воспользоваться формулой (1.3) необходимо определить A и Z искомого ядра. Предположим, что ядро имеет сферическую форму, а зависимость радиуса ядра от массового числа выражается формулой (1.1). Тогда
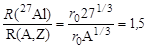 . .
| (1.4.1) |
Решая уравнение (1.4.1), находим, что А = 8. Таким образом, N = Z = 4 и искомое ядро принадлежит нуклиду 8Be. Энергия связи этого ядра (необходимые избытки масс атомов взяты из табл. 1 Приложений):
| ΔW(8Be) = [4·0,007825 -4·0,008665 – 0,005308] ·931,5 = 56,5 МэВ |
Задача 1.5
Найти удельную энергию связи 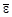 нуклидов 2Н, 6Li, 40Ar, 107Ag, 152Dy (Δ = -0,075271 а.е.м.), 235U и построить график зависимости
нуклидов 2Н, 6Li, 40Ar, 107Ag, 152Dy (Δ = -0,075271 а.е.м.), 235U и построить график зависимости 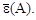
Решение
По определению
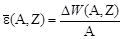 . .
| (1.5.1) |
Вычисления рекомендуется произвести самостоятельно. Для вычисления ΔW(A,Z) следует воспользоваться формулой (1.3) и данными из табл. 1 Приложений. Должны быть получены следующие результаты:
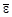 (2Н) = 2,23 МэВ,
(2Н) = 2,23 МэВ, 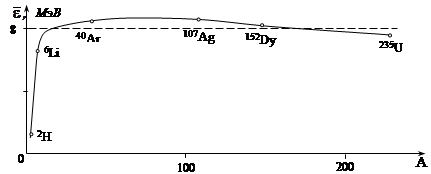
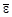 (6Li) = 5,33 МэВ,
(6Li) = 5,33 МэВ, 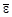 (40Ar) = 8,60 МэВ,
(40Ar) = 8,60 МэВ, 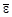 (107Ag) = 8,55 МэВ,
(107Ag) = 8,55 МэВ, 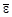 (152Dy) = 8,11 МэВ,
(152Dy) = 8,11 МэВ, 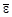 (235U) = 7,59 МэВ.
(235U) = 7,59 МэВ.
Полученная кривая дает примерные величины удельной энергии связи нуклона в МэВ/нуклон для β-стабильных нуклидов.
Задача 1.6
Определить: а) энергию связи нейтрона и α-частицы в ядре 21Ne; б) энергию, необходимую для разделения ядра 16О на четыре одинаковые частицы.
Решение
а) Устойчивое ядро 21Ne образуется при захвате нейтрона ядром 20Ne. Энергия, которая выделяется в этом процессе, численно равна энергии связи нейтрона в ядре 21Ne:
| ΔWn(21Ne) = [Δn + Δ (20Ne) - Δ (21Ne)]·931,5 = = [0,008655 - 0,007560 + 0,006151] ·931,5 = 6,76 МэВ |
Рассуждая подобным же образом, можно считать, что ядро 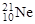 образовалось при слиянии ядер
образовалось при слиянии ядер 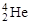 и
и  , а энергия связи α‑частицы в ядре 21Ne равна:
, а энергия связи α‑частицы в ядре 21Ne равна:
| ΔWα(21Ne) = [Δα + Δ (17О) - Δ (21Ne)]·931,5 = = [0,002604 – 0,000867 + 0,006151] ·931,5 = 7,34 МэВ |
б)При разделении ядра 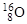 на четыре одинаковых фрагмента образуются ядры с нуклонным составом (4,2), которые являются α-частицами. По общему правилу энергия разделения ядра 16О на четыре α‑частицы равна
на четыре одинаковых фрагмента образуются ядры с нуклонным составом (4,2), которые являются α-частицами. По общему правилу энергия разделения ядра 16О на четыре α‑частицы равна
ΔW4α(16О) = [4Δα - Δ (16О)]·931,5 =
= [4·0,002604 + 0,005085] ·931,5 = 14,4 МэВ
Задача 1.7
Вычислить энергию связи нейтрона в ядре 14N, если известно, что энергии связи ядер 13N и 14N равны 94,10 и 104,66 МэВ.
Решение
Энергия связи нейтрона в ядре 14N равна:
| ΔWn(14N) = mn + Mат(13N) – Mат(14N). | (1.7.1) |
Воспользуемся формулой (1.2) для выражения масс нуклидов 13N и 14N через энергию связи их ядер:
| Mат(13N) = 7mH + (13-7)mn - ΔW(13N), | (1.7.2) |
| Mат(14N) = 7mH + (14-7)mn - ΔW(14N). | (1.7.3) |
Подставив (1.7.2) и (1.7.3) в (1.7.1) получим, что
| ΔWn(14N) = ΔW(14N) - ΔW(13N) = 104,66 – 94,10 = 10,56 МэВ. |
Задача 1.8
Найти энергию, необходимую для разделения ядра 16О на α-частицу и ядро 12С, если известно, что энергии связи ядер 16О, 12С и 4Не равны 127,62; 92,16 и 28,30 МэВ.
Решение
Выкладки, аналогичные тем, которые сделаны в задаче 1.8, приводят к следующему результату:
ΔWα(16О) = ΔW(16О) - ΔW(4Не) - ΔW(12С) =
=127,62 – 92,16 – 28,30 = 7,16 МэВ.
Задача 1.9
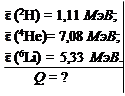 Определить энергию, выделяющуюся при образовании двух α-частиц в результате синтеза ядер 2Н и 6Li, если известно, что энергии связи на один нуклон в ядрах 2Н, 4Не и 6Li равны 1,11; 7,08 и 5,33 МэВ соответственно.
Определить энергию, выделяющуюся при образовании двух α-частиц в результате синтеза ядер 2Н и 6Li, если известно, что энергии связи на один нуклон в ядрах 2Н, 4Не и 6Li равны 1,11; 7,08 и 5,33 МэВ соответственно.
Решение
Запишем схему процесса синтеза:
2Н + 6Li → 4Не + 4Не
По определению, энергия Q, которая освобождается в этом процессе, численно равна разности масс исходной и конечной систем:
| Q = Mат(2H) + Mат(6Li) – 2Mат(4He). | (1.9.1) |
Используя формулу (1.2) для выражения в (1.9.1) масс атомов через их энергию связи (проделать самостоятельно), получим
Q = 2ΔW(4He) - ΔW (2H) - ΔW(6Li) =
= 2·4 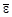 (4Не) - 2 (4Не) - 2 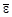 (2Н) - 6 (2Н) - 6 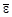 (6Li) =
= 2·4·7,08 - 2·1,11 - 6·5,33 = 22, 44 МэВ (6Li) =
= 2·4·7,08 - 2·1,11 - 6·5,33 = 22, 44 МэВ
|
Задача 1.10
Показать, что для ядра сферической формы с однородной плотностью электрического заряда энергия кулоновского отталкивания протонов Uкул = 0,6kZ2e2/R, где Z и R – заряд и радиус ядра, k – коэффициент пропорциональности, определяемый системой единиц. В СИ k = 9∙109 м/Ф, в СГС k = 1.
Решение
Однородная плотность электрического заряда ядра
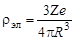 . .
| (1.10.1) |
Работа, совершаемая против сил электрического поля, создаваемого равномерно заряженной сферой радиуса r с зарядом
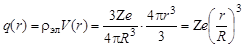 , r ≤ R, , r ≤ R,
| (1.10.2) |
при перемещении заряда dq из бесконечности в точку r будет равна
| dA = [φ(r) - φ∞]∙dq = φ(r) ∙dq, | (1.10.3) |
при условии, что φ∞= 0. В (1.10.3) φ(r) – потенциал электрического поля, создаваемый зарядом q(r) на поверхности сферы радиуса r,
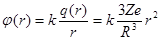 , ,
| (1.10.4) |
если использовать выражение (1.10.2).
Дифференцируя (1.10.2) по r, получим изменение заряда сферы при добавлении заряда 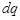 :
:
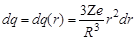 . .
| (1.10.5) |
Подставив (1.10.4) и (1.10.5) в (1.10.3), получим
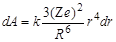 . .
| (1.10.6) |
Поскольку совершаемая работа увеличивает потенциальную энергию ядра, то dA = dU. Поэтому
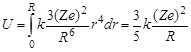 . .
| (1.10.7) |
Задача 1.11
Считая, что разность энергий связи зеркальных ядер[1] 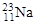 и
и 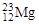 определяется только различием энергий кулоновского отталкивания протонов (см. формулу (1.10.7) в предыдущей задаче), вычислить их радиусы. Сравнить результаты с вычислением радиусов по формуле (1.1).
определяется только различием энергий кулоновского отталкивания протонов (см. формулу (1.10.7) в предыдущей задаче), вычислить их радиусы. Сравнить результаты с вычислением радиусов по формуле (1.1).
Решение
Разность энергий кулоновского отталкивания протонов в ядрах 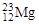 и
и 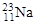 согласно формуле (1.10.7) будет равна
согласно формуле (1.10.7) будет равна
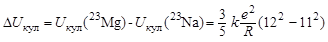 . .
| (1.11.1) |
В (1.11.1) принято, что в соответствии с (1.1) радиус ядра не зависит от Z и определяется только величиной массового числа А.
Из этого выражения находим, что
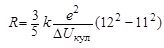 . .
| (1.11.2) |
По условию задачи уменьшение энергии связи ядра 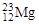 относительно энергии связи ядра
относительно энергии связи ядра 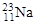 обусловлено большей энергией кулоновского отталкивания протонов в ядре
обусловлено большей энергией кулоновского отталкивания протонов в ядре 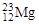 при одинаковой энергии ядерного взаимодействия. Поэтому
при одинаковой энергии ядерного взаимодействия. Поэтому
| ΔUкул= ΔW(23Na) - ΔW(23Mg). | (1.11.3) |
Используя формулу (1.3) для ΔW(A,Z) вычислим ΔUкул в (1.11.3):
| ΔUкул= [Δn - ΔH + Δ(23Mg) - Δ(23Na)]·931,5 = = [ 0,008665 – 0,007825 – 0,005865 + 0,010227] ·931,5 = 4,85 МэВ |
Подставляя полученное значение ΔUкул= 4,85 МэВ в (1.1,1.2), определим величину R:
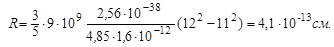
|
Расчет величины R (выполнить самостоятельно) по формуле (1.1) дает 4·10-13см, что хорошо согласуется с найденной выше величиной радиуса ядра.
Задача 1.12
Вычислить с помощью полуэмпирической формулы (1.4): а) энергии связи ядер 40Са и 107Ag; б) энергии связи на один нуклон в ядрах 50V и 200Hg; в) массы атомов 45Sc и 70Zn.
Решение
а) У ядра40Са Z =20, поэтому четвертый член в формуле (1.4) равен нулю, а пятый следует взять со знаком плюс. Тогда
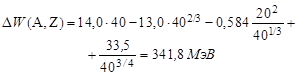
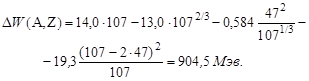 |
Ядро 107Ag имеет Z = 47. Пятый член в формуле (1.4) равен нулю.
Справочные значения искомых величин: 342,06 и 915,27 МэВ.
б) Этот пункт рекомендуется проделать самостоятельно.
Указание: для вычисления энергии связи на один нуклон в ядрах 50V и 200Hg необходимо с помощью формулы (1.4) найти полную энергию связи этих ядер и разделить ее на соответствующее массовое число (см. формулу (1.5.1)). Должны быть получены следующие значения: 8,65 и 7,81 МэВ. Табличные значения: 8,70 и 7,91 МэВ.
в) Массы атомов выразим из формулы (1.2):
| Mат(A,Z) = Z·mH + (A - Z)·mn – ΔW(A,Z). | (1.12.1) |
Подставив в (1.12.1) энергию связи из формулы (1.4) получим рабочую формулу для нахождения масс атомов:
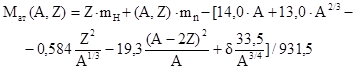
| (1.12.2) |
Вычисления масс атомов 45Sc и 70Zn по формуле (1.12.2) (проделать самостоятельно) дают следующие значения: 44,955 и 69,932 а.е.м. Справочные значения: 44,956 и 69,925 а.е.м.
Задача 1.13
Определить с помощью формулы (1.4) заряд ядра, имеющего наименьшую массу среди ядер с одинаковым нечетным значением массового числа А. Предсказать с помощью полученной формулы характер активности (электронная или позитронная) следующих β-активных ядер: 103Ag; 127Sn и 141Cs.
Решение
Согласно формуле (1.12.1) ядрам с наибольшей энергией связи отвечает наименьшая масса. Поэтому для ядер изобаров (нуклидов с одинаковыми массовыми числами А) всегда имеется ядро с Z0, имеющее наименьшую массу. Для нахождения Z0 вычислим частную производную от (1.12.2) и результат приравняем нулю:
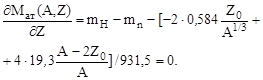
| (1.13.1) |
Подставив в (1.13.1) массу атома Н и массу нейтрона в а.е.м., и решая относительно Z0, получим
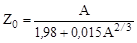 . .
| (1.13.2) |
Если для заданного нуклида (A,Z) расчет по формуле (1.13.2) дает Z0 > Z, то для увеличения Z ядро должно испытывать β--распад, если же Z0 < Z, то β+-распад.
Ядро 103Ag: Z =47, а
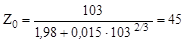 . .
|
Следовательно, Z0 < Z и ядро 103Ag должно испытывать β+-распад.
Ядро 127Sn: Z = 50, а
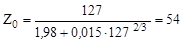 . .
|
Следовательно, Z0 > Z и ядро 127Sn должно испытывать β--распад.
Ядро 141Cs: Z = 55, а
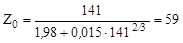 . .
|
Следовательно, Z0 > Z и ядро 141Cs должно испытывать β--распад.
Задача 1.14
Сколько компонент сверхтонкой структуры имеют в основном состоянии следующие атомы: 3H(2S1/2); 6Li(2S1/2); 9Be(1S0); 15N(4S3/2) 35Cl(2P3/2). В скобках указан основной терм электронной оболочки.
Решение
Число N линий сверхтонкого расщепления оптических спектров будет равно (в соответствии с (1.5)) 2I + 1, если J ≥ I; или 2J + 1, если J < I. С помощью табл. 1 Приложений устанавливаем спины I ядер, а с помощью термов электронной оболочки – механические моменты J электронной оболочки соответствующего атома. Построим следующую таблицу, которая дает ответ на поставленные вопросы:
| Нуклид | I | J | N |
| 3H | 1/2 | 1/2 | 2I + 1 = 2(1/2) + 1 = 2 |
| 6Li | 1/2 | 2J + 1 = 2(1/2) + 1 = 2 | |
| 9Be | 3/2 | 2J = 1 = 2(0) +1 = 1 | |
| 15N | 1/2 | 3/2 | 2I + 1 = 2(1/2) + 1 = 2 |
| 35Cl | 3/2 | 3/2 | 2I + 1 = 2(3/2) + 1 = 4 |
Задача 1.15
Определить спин ядра 59Со, основной терм атома которого 4F9/2 содержит восемь линий сверхтонкого расщепления.
Решение
Механический момент J атома 59Со равен 9/2, как следует из приведенного терма. Значит (см. предыдущую задачу 1.14), если J < I, то число линий сверхтонкого расщепления должно быть равно 2J + 1 = 2(9/2) + 1 = 10. Поскольку имеем восемь линий, то заключаем, что J > I и 2I + 1 = 8, откуда I = 7/2.
Задача 1.16
Терм 2D3/2 атома 209Bi имеет четыре линии сверхтонкого расщепления, причем отношение интервалов между соседними линиями равно 6 : 5 : 4. Найти с помощью правила интервалов спин ядра, а также число компонент сверхтонкого расщепления линии 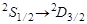 .
.
Решение
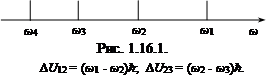 Если предположить, что J ≥ I, то 2I + 1=4, откуда I = 3/2, т.е. совпадает с J. Поэтому можно только утверждать, что I ≥ 3/2 и необходима дополнительная информация. Воспользуемся правилом интервалов (рис. 1.16.1). Интервалом называется расстояние между двумя соседними линиями сверхтонкого расщепления, выраженное в разности частот, или энергий. Согласно этому правилу (см. рис. 1.16.1)
Если предположить, что J ≥ I, то 2I + 1=4, откуда I = 3/2, т.е. совпадает с J. Поэтому можно только утверждать, что I ≥ 3/2 и необходима дополнительная информация. Воспользуемся правилом интервалов (рис. 1.16.1). Интервалом называется расстояние между двумя соседними линиями сверхтонкого расщепления, выраженное в разности частот, или энергий. Согласно этому правилу (см. рис. 1.16.1)
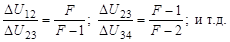
| (1.16.1) |
Для I = J = 3/2 правило интервалов дает отношение
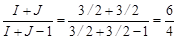 ,
,
которое оказывается меньше, чем по условию задачи. Отсюда следует, что I > 3/2. Поэтому для определения спина ядра I нужно решить уравнение
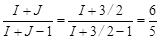 ,
,
из которого получаем I = 9/2.
Задача 1.17
Отношение интенсивностей линий сверхтонкого расщепления при переходе 2P1/2 → 2S1/2 атома натрия равно приблизительно 10 : 6. Имея в виду, что сверхтонкая структура вызвана расщеплением терма 2S1/2 (расщепление терма 2P1/2 ничтожно мало), найти спин ядра 23Na.
Решение
Отношение интенсивностей линий сверхтонкого расщепления равно отношению статистических весов (1.6) появления каждого из возможных значений вектора 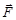 (подуровней расщепления):
(подуровней расщепления):
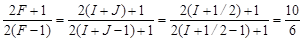 .
.
Из этого уравнения находим, что I = 3/2.
Задача 1.18
С помощью модели ядерных оболочек (рис. 1.1) написать конфигурацию основных состояний ядер: 6Li, 13C и 25Mg.
Решение
Для обозначения суммарного орбитального момента L электронов в атомных термах используют заглавные буквы S(L = 0), P(L = 1), D(L = 2), F(L = 3), . . . и далее латинский алфавит. При обозначении орбитального момента l нуклона в ядре используют строчные буквы s(l = 0), p(l = 1), d(l = 2), f(l = 3), . . , и далее латинский алфавит. Во всем другом запись атомных термов и состояний нуклонов в ядрах совпадают.
Ядро 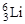 . В состоянии 1s1/2 находятся два протона и два нейтрона, а в состоянии 1p3/2 – один протон и один нейтрон. Следовательно, конфигурация основного состояния ядра
. В состоянии 1s1/2 находятся два протона и два нейтрона, а в состоянии 1p3/2 – один протон и один нейтрон. Следовательно, конфигурация основного состояния ядра 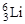 записывается следующим образом: (1s1/2)4(1p3/2)2, где верхние правые индексы указывают число нуклонов в данном состоянии.
записывается следующим образом: (1s1/2)4(1p3/2)2, где верхние правые индексы указывают число нуклонов в данном состоянии.
Ядро 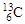 . В состоянии 1s1/2 находятся два протона и два нейтрона, а в состоянии 1p3/2 – четыре протона и четыре нейтрона и в состоянии 1p1/2 – один нейтрон. Следовательно, ядро
. В состоянии 1s1/2 находятся два протона и два нейтрона, а в состоянии 1p3/2 – четыре протона и четыре нейтрона и в состоянии 1p1/2 – один нейтрон. Следовательно, ядро 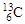 в основном состоянии имеет следующую конфигурацию: (s1/2)4(p3/2)8p3/2.
в основном состоянии имеет следующую конфигурацию: (s1/2)4(p3/2)8p3/2.
Ядро 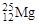 . В состоянии 1s1/2 находятся два протона и два нейтрона, а в состоянии 1p3/2 – четыре протона и четыре нейтрона, в состоянии 1p1/2 – два протона и два нейтрона и в состоянии 1d5/2 – четыре протона и пять нейтронов. Следовательно, ядро
. В состоянии 1s1/2 находятся два протона и два нейтрона, а в состоянии 1p3/2 – четыре протона и четыре нейтрона, в состоянии 1p1/2 – два протона и два нейтрона и в состоянии 1d5/2 – четыре протона и пять нейтронов. Следовательно, ядро 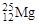 в основном состоянии имеет следующую конфигурацию: (s1/2)4(p3/2)8(p3/2)4(d5/2)9.
в основном состоянии имеет следующую конфигурацию: (s1/2)4(p3/2)8(p3/2)4(d5/2)9.
Задача 1.19
Определить с помощью модели ядерных оболочек спины и четности основных состояний ядер: 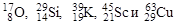 .
.
Решение
При решении задачи будем руководствоваться следующими правилами, которые являются следствиями из модели оболочек:
1. Суммарный механический момент нуклонов одного рода в заполненных оболочках равен нулю.
2. Один из «лишних» нуклонов, сверх заполненного уровня, имеет механический момент следующего уровня и определяет спин и четность ядра.
3. Один из «недостающих» до заполнения уровня нуклон («дырка») имеет механический момент этого уровня и определяет спин и четность ядра.
4. Нуклоны одного уровня объединяются в пары с нулевым механическим моментом.
Для решения задачи необходимо иметь перед глазами схему уровней, получаемых с помощью модели ядерных оболочек.
Ядро  . Суммарный механический момент протонов равен нулю, т.к. ядро содержит четное число протонов. Нейтронами полностью заполнены уровни, включая 1р1/2. Лишний нейтрон находится на уровне 1d5/2. Поэтому спин ядра I = 5/2. Орбитальный момент лишнего нуклона l = 2. Следовательно, четность ядра
. Суммарный механический момент протонов равен нулю, т.к. ядро содержит четное число протонов. Нейтронами полностью заполнены уровни, включая 1р1/2. Лишний нейтрон находится на уровне 1d5/2. Поэтому спин ядра I = 5/2. Орбитальный момент лишнего нуклона l = 2. Следовательно, четность ядра
P = (‑1)l = (-1)2 = +1.
Ядро 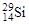 . Суммарный механический момент протонов равен нулю, т.к. ядро содержит четное число протонов. Нейтронами полностью заполнены уровни, включая 1d1/2 Лишний нейтрон находится на уровне 2s1/2. Поэтому спин ядра I = 1/2. Орбитальный момент лишнего нуклона l = 0. Следовательно, четность ядра
. Суммарный механический момент протонов равен нулю, т.к. ядро содержит четное число протонов. Нейтронами полностью заполнены уровни, включая 1d1/2 Лишний нейтрон находится на уровне 2s1/2. Поэтому спин ядра I = 1/2. Орбитальный момент лишнего нуклона l = 0. Следовательно, четность ядра
P = (‑1)l = (-1)0 = +1.
Ядро 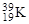 . Нейтронами полностью заполнены уровни, включая 1d3/2. Недостает одного протона («дырка») до заполнения уровня 1d3/2. Орбитальный момент дырки l = 2. Следовательно, спин ядра I = 3/2, а четность
. Нейтронами полностью заполнены уровни, включая 1d3/2. Недостает одного протона («дырка») до заполнения уровня 1d3/2. Орбитальный момент дырки l = 2. Следовательно, спин ядра I = 3/2, а четность
P = (‑1)l = (-1)2 = +1.
Ядро 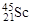 . Суммарный механический момент нейтронов равен нулю, т.к. ядро содержит четное число нейтронов. Протонами полностью заполнены уровни, включая 1d3/2, но имеется один нуклон на уровне 1f7/2. Орбитальный момент лишнего нуклона l = 3. Следовательно, спин ядра I = 7/2, а четность
. Суммарный механический момент нейтронов равен нулю, т.к. ядро содержит четное число нейтронов. Протонами полностью заполнены уровни, включая 1d3/2, но имеется один нуклон на уровне 1f7/2. Орбитальный момент лишнего нуклона l = 3. Следовательно, спин ядра I = 7/2, а четность
P = (‑1)l = (-1)3 = -1.
Ядро 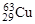 . Суммарный механический момент нейтронов равен нулю, т.к. ядро содержит четное число нейтронов. Протонами полностью заполнены уровни, включая 1f7/2, но имеется один протон на уровне 1p3/2. Следовательно, спин ядра I = 3/2, а четность
. Суммарный механический момент нейтронов равен нулю, т.к. ядро содержит четное число нейтронов. Протонами полностью заполнены уровни, включая 1f7/2, но имеется один протон на уровне 1p3/2. Следовательно, спин ядра I = 3/2, а четность
P = (‑1)l = (-1)1 = -1.
Задача 1.20
Некоторые ядра обладают квадрупольным электрическим моментом Q, что указывает на отклонение распределения заряда от сферически симметричного. Для определенности полагают форму ядра в виде эллипсоида вращения с полуосями b (по спину ядра) и а (перпендикулярно спину ядра). Оценить степень несферичности ядра 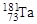 , имеющего одно из наибольших значений квадрупольного момента Q = +6·10-24 см2. Для оценки вычислить отношение b/a.
, имеющего одно из наибольших значений квадрупольного момента Q = +6·10-24 см2. Для оценки вычислить отношение b/a.
Решение
Для ядра, имеющего форму эллипсоида вращения с однородной объемной плотностью электрического заряда, квадрупольный электрический момент равен
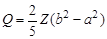 ,
,
откуда
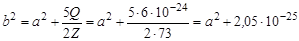 . .
| (1.20.1) |
Объем эллипсоида вращения
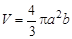 .
.
Приравниваем этот объем объему недеформированного ядра сферической формы (ядерное вещество несжимаемо!) с таким же числом нуклонов и радиусом, даваемый формулой (1.1), получим уравнение
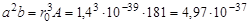 см3,
см3,
или
 . .
| (1.20.2) |
Подставив (1.20.2) в (1.20.1) получаем кубическое уравнение для нахождения величины b. После нахождения b с помощью (1.20.2) определяется величина а. Однако такой способ решения сложен и трудоемок. Значительно проще решать систему уравнений
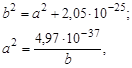
| (1.20.3) |
методом последовательных приближений. В качестве первого приближения полагаем, что
b = Rя = 1,4·10-13·A1/3 = 1,4·10-13·1811/3 ≈ 8·10-13 см.
Подставляем это значение во второе уравнение системы (1.20.3) и находим первое приближение для а2. Затем, полученное значение а2 подставляем в первое уравнение системы (1.20.3) и находим второе приближения для b, которое подставляем во второе уравнение системы (1.20.3) и находим второе приближение для а2, и т.д. Процесс быстро сходится, и в результате получаем b = 8,78·10-12 см; а = 7,52·10-13 см.
Окончательно, искомое отношение
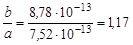 .
.
Задача 1.21
Определить значения изоспина Т основных состояний ядер изотопов углерода 10C, 11C, 12C, 13C, 14C.
Решение
В основном состоянии ядра значение изоспина 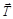 совпадает с модулем проекции изоспина Т = | Тz |. Проекция изоспина Тz ядра, состоящего из Z протонов и N нейтронов, равна
совпадает с модулем проекции изоспина Т = | Тz |. Проекция изоспина Тz ядра, состоящего из Z протонов и N нейтронов, равна
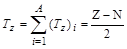 , ,
| (1.22.1) |
то есть для основных состояний ядер Т = |Z - N|/2.
Следовательно, значение изоспина будет равно:
для 10C - I = (6 – 4)/2 = 1,
для 11C - I = (6 – 5)/2 = 1/2,
для 12C - I = (6 – 6)/2 = 0,
для 13C - I = (7 – 6)/2 = 1/2,
для 14C - I = (8 – 6)/2 = 1.
Задачи для самостоятельного решения.
1.22. Оценить, во сколько раз объем ядра 238U больше объема ядра 4Не. Каковы размеры этих ядер и как соотносятся их радиусы?
1.23. Оценить среднее расстояние между центрами нуклонов в ядре, считая, что ядро имеет сферическую форму.
1.24. Природный хлор состоит из двух нуклидов: 35Cl и 37Cl. Атомное содержание нуклида Сат(35Cl) = 75,53%. Найти атомную массу природного хлора.
1.25. Сравнить дефект массы δ ядра 12С в а.е.м. с избытком масс Δ этого нуклида. Чем объясняется различие этих величин?
1.26. Найти энергию связи α-частицы в ядре 40Са. Ar(40Ca) = 39,96259 а.е.м.
1.27. Определить энергию, которая высвобождается при синтезе ядер 4Не из ядер дейтерия и свободных нуклонов.
1.28. Вычислить удельную энергию связи 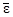 для нуклидов 2Н, 3Н, 3Не, 4Не, 6Li, 8Be, 12C, 16О и 17F. Изобразить графически полученную зависимость
для нуклидов 2Н, 3Н, 3Не, 4Не, 6Li, 8Be, 12C, 16О и 17F. Изобразить графически полученную зависимость 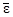 от массового числа и объяснить результаты.
от массового числа и объяснить результаты.
1.29. Энергия связи ядра, состоящего из трех протонов и четырех нейтронов, равна 39,249 МэВ. Какому нуклиду принадлежит это ядро? Определить в а.е.м. массу ядра этого нуклида. Учесть, что масса протона mp = 938,26, а масса нейтрона mn = 939,55 МэВ.
1.30. Какую наименьшую энергию надо затратить, чтобы удалить из ядра 14N один из протонов или один из нейтронов.
1.31. Определить разность энергий связи нейтрона и протона в ядре 10В. Объяснить причину различия их энергии связи.
1.32. Как отличается энергия отделения одного нейтрона от ядра 9Ве и удельная энергия связи этого ядра.
1.33. Считая, что различие энергий связи ядер изобаров 13N и 13С обусловлено только кулоновской энергией взаимодействия между протонами, найти энергию, выделяющуюся в процессе
13N → 13С + β+ + ν.
Указание. Массу нейтрино считать равной нулю. Воспользоваться данными, полученными в задаче 1.10. (Ответ: Q = (mp – mn) - me + 0,6ke2[Z2(13N)- Z2(13С)]/R).
1.34. Для ядра 41Sc определить с помощью формулы Вейцзеккера (1.4): а) энергию отделения нейтрона; б) энергию отделения протона. В чем причина столь большого различия этих величин?
1.35. Используя формулу Вейцзеккера (1.4), предсказать нуклиды, устойчивые по отношению к β-распаду для изобаров с массовыми числами 20, 40, 80, 120 и 200. Для найденных нуклидов построить зависимость Z(N) (т.н. «дорожку стабильности»).
1.36. Какой тип β-распада испытывает нуклид 135Те? Какая энергия при этом выделяется? Задачу решить, используя формулу Вейцзеккера (1.4).
1.37. С помощью формулы Вейцзеккера (1.4) определить радиус R ядра 109Ag и константу r0 в формуле (1.1).
Указание. Использовать формулу (1.10.7).
1.38. Определить спин ядра, если при переходе атома из состояния 3P0 в 3S1 наблюдается две линии сверхтонкого расщепления.
1.39. Атом 209Bi находится в состоянии 2D1/2. Спин его ядра I = 9/2. Вычислить квантовые числа вектора 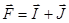 суммарного момента атома, где
суммарного момента атома, где 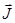 - полный механический момент электронной оболочки.
- полный механический момент электронной оболочки.
1.40. Найти величину изотопического спина 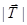 и его проекции
и его проекции 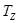 для ядер 1Н, 2Н, 3Не и 4Не.
для ядер 1Н, 2Н, 3Не и 4Не.
1.41. Используя модель атомных оболочек вычислить спины основных состояний ядер 7Li, 15N, 32S, 39K. Сравнить полученные значения с табличными и определить четности волновых функций этих ядер в основном состоянии.
Ответы
1.22. 60 раз. R(238U)/R(4He) = 4. 1.23. ~2 Фм. 1.24. 35,460 а.е.м. 1.25. 0,098940 а.е.м. 1.26. 7,044 МэВ. 1.27. 4,45 МэВ. 1.28. 1,11; 2,83; 2,57; 7.07; 5,33; 7,06; 7.68; 7,98 и 7,54 МэВ. 1.29. 7,014360 а.е.м. 1.30. Sр = 7,55 МэВ; Sn = 10,55 МэВ. 1.31. 1,85 МэВ. 1.32. 10,19 МэВ. 1.33. 1,6 МэВ. 1.34. а) 16,42 МэВ; б) 1,76 МэВ. 1.35. 10, 19, 35, 51, 80. 1.36. β‑-распад; 4,8 МэВ. 1.37. R = 7,1 Фм; r0 = 1,5 Фм. 1.38. I = 1/2. 1.39. F = 5; 4. 1.40. 1/2; +1/2; 0; 1/2; +1/2; 0. 1.41. 3/2 ; 1/2- ; 0+ ; 3/2+.
Дата добавления: 2016-06-13; просмотров: 11470;
