Радиоактивные превращения ядер
Основной закон радиоактивного распада:
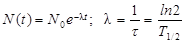 , ,
| (2.1) |
где: N(t) – ожидаемое количество радиоактивных ядер к моменту времени t; N0 – число радиоактивных ядер в момент времени t = 0; λ – постоянная распада; τ – среднее время жизни радиоактивных ядер; Т1/2 – их период полураспада.
Активность
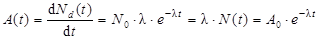 , ,
| (2.2) |
где: Nd(t) – число ядер, которое должно распасться к моменту времени t; А0 – активность в начальный момент времени t = 0. Остальные обозначения те же, что и формуле (2.1).
Закон накопления числа радиоактивных ядер при активации:
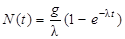 , ,
| (2.3) |
где g - среднее число радиоактивных ядер, образующихся в единицу времени (скорость активации).
Вековое равновесие:
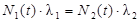 , ,
| (2.4) |
если λ2 >> λ1 и t >> Т1/2. Индекс «1» относится к материнским ядрам, индекс «2» - к дочерним.
Биномиальный закон распределения вероятностей (формула Бернулли) для радиоактивного распада
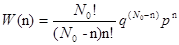
| (2.5) |
позволяет вычислить вероятность распада за время t точно n ядер, если в начальный момент времени их было N0. Вероятности p(t) и q(t) (см. задачу 2.1) равны соответственно
| р(t) =1 – e-λt, | (2.6) |
| q(t) = e-λt. | (2.7) |
Распределение Пуассона:
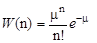 , ,
| (2.8) |
где W(n) – вероятность совершения точно n случайных событий в течение некоторого промежутка времени; μ – математическое ожидание случайной величины. Распределение Пуассона можно использовать, если μ << N0, где N0 - возможное число случайных событий (генеральная совокупность, например, число радиоактивных ядер).
Дисперсия распределения Пуассона
| D ≡ σ2 = μ, | (2.9) |
или средняя квадратичная погрешность (отклонение)
σ = 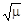 . .
| (2.10) |
Распределение Гаусса или нормальное распределение:
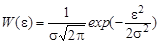 , ,
| (2.11) |
где ε = |n - μ| - отклонение случайной величины n от математического ожидания случайной величины; σ – среднее квадратичное отклонение случайной величины n от математического ожидания μ.
Средняя квадратичная погрешность суммы или разности независимых случайных величин:
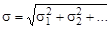 , ,
| (2.12) |
где σi – среднее квадратичное отклонение отдельной случайной величины ni.
Погрешность функции f случайных аргументов х1, х2, … :
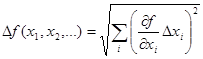 , ,
| (2.13) |
где 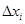 - погрешность соответствующего аргумента.
- погрешность соответствующего аргумента.
Кулоновская функция U(r), выраженная в единицах МэВ, для частицы с зарядом z:
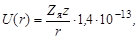
| (2.14) |
где Zя – атомный номер дочернего ядра, а r выражено в см.
Формула для расчета высоты кулоновского барьера в точке r = Rя, если использовать формулу (1.1):
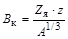 , МэВ. , МэВ.
| (2.15) |
Дата добавления: 2016-06-13; просмотров: 1659;
