Статистика регистрации ядерного излучения
Задача 2.34
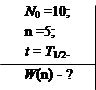 В результате активации образовалось N0 = 10 радиоактивных ядер. Какова вероятность распада точно 5 ядер за время t = Т1/2?
В результате активации образовалось N0 = 10 радиоактивных ядер. Какова вероятность распада точно 5 ядер за время t = Т1/2?
Решение
Используя биномиальный закон (2.5) и формулы (2.6) и (2.7), получим
 .
.
Задача 2.35
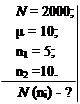 Предполагается провести 2000 измерений активности препарата в течение одинаковых промежутков времени. Среднее число импульсов за время одного измерения равно 10,0. Считая время измерения малым по сравнению с периодом полураспада исследуемого радионуклида, определить число измерений, в которых следует ожидать точно 10 и 5 импульсов.
Предполагается провести 2000 измерений активности препарата в течение одинаковых промежутков времени. Среднее число импульсов за время одного измерения равно 10,0. Считая время измерения малым по сравнению с периодом полураспада исследуемого радионуклида, определить число измерений, в которых следует ожидать точно 10 и 5 импульсов.
Решение
Ожидаемое число измерений, в которых может быть зафиксировано точно ni импульсов будет равно
N (ni) = N·P(ni),
где P(ni) - вероятность появления точно ni импульсов, число которых пропорционально количеству распадающихся ядер за этот же промежуток времени.
Эта вероятность определяется с помощью биномиального закона распределения вероятностей (2.5), если известно полное число возможных событий N0 и время t каждого измерения. Но величины N0 и t неизвестны, и использовать формулу (2.5) не представляется возможным. Однако в случае n << N0 и t << T1/2 биномиальный закон распределения вероятностей (2.5) может быть представлен в виде распределения Пуассона (2.8). Тогда
N (ni) = N 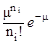 ,
,
и
N (n1) = 2000 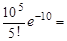 76;
76;
N (n2) = 2000  .
.
Задача 2.36
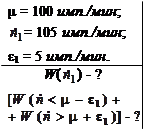 Среднее значение скорости счета импульсов от исследуемого радионуклида с большим периодом полураспада составляет 100,0 имп./мин. Определить вероятность получения 105 имп./мин. И вероятность того, что абсолютное отклонение от среднего числа имеет значение, большее 5,0 имп./мин.
Среднее значение скорости счета импульсов от исследуемого радионуклида с большим периодом полураспада составляет 100,0 имп./мин. Определить вероятность получения 105 имп./мин. И вероятность того, что абсолютное отклонение от среднего числа имеет значение, большее 5,0 имп./мин.
Решение
Согласно условию задачи предполагаем, что время проведения измерений существенно меньше периода полураспада исследуемого радионуклида и для вычисления искомых вероятностей можно воспользоваться распределением Пуассона (2.8). Однако использование формулы (2.8) технически затруднительно, так как связано с вычислением факториалов больших чисел и возведением чисел в степени с большими показателями. Получить более удобную для вычислений форму можно, если воспользоваться утверждением центральной предельной теоремы (ЦПТ) теории вероятности, согласно которой при μ >> 1 распределение Пуассона переходит в нормальное распределение с дисперсией, равной μ:
 . .
| (2.36.1) |
Тогда
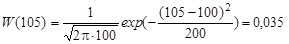 .
.
Очевидно, что сумма вероятностей появления любого значения скорости счета импульсов от 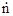 = 0 и до
= 0 и до 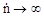 равняется единице. Тогда
равняется единице. Тогда
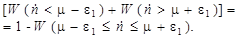
| (2.36.2) |
Используя формулу (2.36.1), вычислим
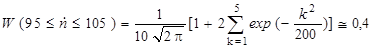 . .
|
Таким образом,
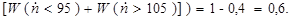
|
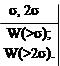 Задача 2.37
Задача 2.37
Вычислить вероятность получения абсолютной погрешности измерения, превосходящей: а) σ и б) 2σ, где σ – среднеквадратичная погрешность.
Решение
Предполагаем, что случайная величина имеет нормальный закон распределения. Тогда искомая вероятность будет равна
 . .
| (2.37.1) |
Если в интеграле произвести замены:
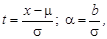
|
то получим
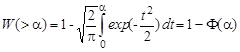 , ,
|
где Ф(α) – интеграл ошибок, который не выражается в элементарных функциях и значения которого можно найти в подробных таблицах. Для поставленной задачи α =1 и α = 2 и соответственно: Ф(1) = 0,683; Ф(2) = 0,955.
Задача 2.38
 Счетчик, находящийся в поле исследуемого излучения, зарегистрировал 3600 импульсов за 10 мин. Найти: а) среднюю квадратичную погрешность в скорости счета; б) продолжительность измерения, обеспечивающую определение скорости счета с погрешностью 1,00%.
Счетчик, находящийся в поле исследуемого излучения, зарегистрировал 3600 импульсов за 10 мин. Найти: а) среднюю квадратичную погрешность в скорости счета; б) продолжительность измерения, обеспечивающую определение скорости счета с погрешностью 1,00%.
Решение
По определению средняя скорость счета
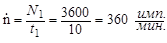 .
.
Погрешность измерения числа импульсов является принципиально неустранимой, так как вызвана статистическим характером распада большого числа радиоактивных ядер. Измерение же времени обычно выполняется с относительной погрешностью, существенно меньшей, чем при измерении числа импульсов, и потому ее величиной можно пренебречь. Тогда, если предположить, что условия применения распределения Пуассона выполнены, можно воспользоваться формулой (2.10) и
 .
.
Относительная погрешность измерения числа импульсов
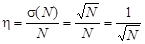 .
.
Следует отметить, что эта погрешность соответствует доверительной вероятности 68%. Если использовать значение доверительной вероятности 95%, как принято в настоящее время, то полученную величину надо удвоить (см. предыдущую задачу):
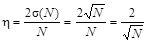 .
.
Тогда число импульсов, которое необходимо зарегистрировать для получения заданной относительной точности с доверительной вероятностью 95%, составит
 .
.
Необходимое время измерений составит
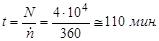
Задача 2.39
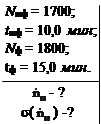 При изучении интенсивности исследуемого облучения (вместе с фоном) счетчик зарегистрировал 1700 имп. за 10,0 мин. Отдельное измерение фона дало 1800 имп. за 15,0 мин. Найти скорость счета, имп./мин, обусловленную исследуемым облучением, и ее среднюю квадратичную погрешность.
При изучении интенсивности исследуемого облучения (вместе с фоном) счетчик зарегистрировал 1700 имп. за 10,0 мин. Отдельное измерение фона дало 1800 имп. за 15,0 мин. Найти скорость счета, имп./мин, обусловленную исследуемым облучением, и ее среднюю квадратичную погрешность.
Решение
Фоном принято называть излучение, не связанное с исследуемым излучением, действие которого на счетчик не представляется возможным исключить. Поэтому
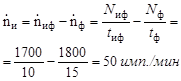
Средняя квадратичная погрешность искомой скорости счета будет равна, согласно (2.9) и (2.12):
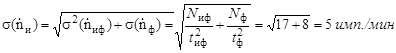
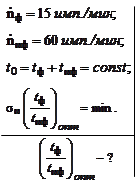 Задача 2.40
Задача 2.40
Скорость счета импульсов от фона составляет 15 имп./мин, а скорость счета от исследуемого препарата и фона составляет 60 имп./мин. Пусть tф и tиф – время измерения фона и исследуемого препарата при наличии фона. Найти оптимальное отношение tф/tиф, при котором точность определения скорости счета от самого препарата будет максимальной для заданного полного времени tф + tиф.
Решение
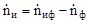
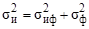 ,
,
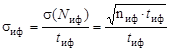 ;
;
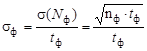 ;
;
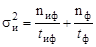 . .
| (2.40.1) |
Для нахождения отношения tф/tиф, которое отвечает минимальному значению σи, вычислим полный дифференциал от (2.40.1) и приравняем его к нулю. Имеем
 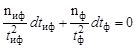 . .
| (2.40.2) |
Из условия 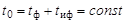 следует, что
следует, что
 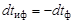 . .
| (2.40.3) |
Подставив (2.30.3) в (2.40.2), получим
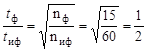 .
.
Задача 2.41
 Счетчик Гейгера-Мюллера с разрешающим временем τ = 0,20 мс зарегистрировал 3,0·104 имп./мин. Оценить среднее число частиц, прошедших через счетчик в мин.
Счетчик Гейгера-Мюллера с разрешающим временем τ = 0,20 мс зарегистрировал 3,0·104 имп./мин. Оценить среднее число частиц, прошедших через счетчик в мин.
Решение
 Любой счетчик ядерного излучения после регистрации попавшей частицы затрачивает некоторый промежуток времени τ для восстановления своих свойств. Время τ – время восстановления является одной из основных характеристик счетчика ядерных частиц. Если в течение этого промежутка времени в счетчик попадает частица, то она не может быть зарегистрирована. Рисунок поясняет это явление. Частицы 1, 2, 4 будут зарегистрированы, а частица 3 – нет (просчитана), так как она попала в счетчик в интервал времени τ восстановления свойств счетчика.
Любой счетчик ядерного излучения после регистрации попавшей частицы затрачивает некоторый промежуток времени τ для восстановления своих свойств. Время τ – время восстановления является одной из основных характеристик счетчика ядерных частиц. Если в течение этого промежутка времени в счетчик попадает частица, то она не может быть зарегистрирована. Рисунок поясняет это явление. Частицы 1, 2, 4 будут зарегистрированы, а частица 3 – нет (просчитана), так как она попала в счетчик в интервал времени τ восстановления свойств счетчика.
Пусть время измерения t >> τ . Тогда среднее число частиц N0, прошедших через счетчик за это время, можно представит следующим образом:
 N0 = N + ΔN, N0 = N + ΔN,
| (2.41.1) |
где N >> 1 – число частиц, зарегистрированных за время t; ΔN = 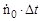 – число просчитанных (незарегистрированных) частиц за суммарное мертвое время
– число просчитанных (незарегистрированных) частиц за суммарное мертвое время
 Δt = τN = Δt = τN = 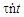 , ,
| (2.41.2) |
так как τN – суммарное время, в течение которого счетчик не мог регистрировать частицы. Тогда
 N0 = N + N0 = N + 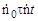 . .
| (2.41.3) |
Разделив левую и правую части уравнения (2.41.3) на t, получим
 . .
| (2.41.4) |
Из последнего уравнения
 имп./мин.
имп./мин.
Задача 2.42
 Какая доля частиц, проходящих через счетчик с разрешающим временем τ =1,0 мкс, не будет зарегистрирована при скорости счета
Какая доля частиц, проходящих через счетчик с разрешающим временем τ =1,0 мкс, не будет зарегистрирована при скорости счета  и 1,0·105 имп./мин.
и 1,0·105 имп./мин.
Решение
Количество просчитанных импульсов (используем формулу (2.41.3) из предыдущей задачи) равно
 .
.
Тогда
η1 = 100·1,0·10-6= 10-4 = 0,01%
η2 = 105·1,0·10-6 = 0,1 = 10%
Дата добавления: 2016-06-13; просмотров: 4204;
