Вимоги до математичних моделей

Найважливішою вимогою до математичної моделі є вимога її адекватності(відповідності) об’єкту-оригіналу відносно вибраної системи його характеристик. Під цим, як правило розуміють: 1) правильний якісний опис об’єкта за вибраними характеристиками; 2) правильний кількісний опис об’єкта за вибраними характеристиками з необхідною точністю в розумних межах. Отже, під адекватністю ММ будемо розуміти можливість відображення заданих властивостей моделі з заданою точністю. Точність визначається як степінь співпадіння вихідних параметрів моделі та об’єкту-оригінала.

Оберненою величиною до точності моделі є її похибка. Для прикладу, відносна похибка моделі 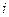-го вихідного вихідного параметра визначається з виразу [4]

,

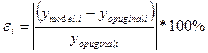де 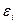– похибка моделі 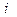-го вихідного вихідного параметра, 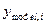– значення 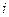-го вихідного вихідного параметра порахованого з використанням побудованої моделі, а 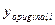– значення 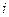-го вихідного вихідного параметра порахованого з використанням об’єкту-оригіналу.

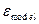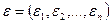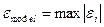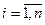При визначенні похибки математичної моделі використовується одна з норм вектора , а саме: , де , або .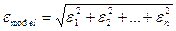

Розглянемо, для прикладу, побудовану математичну модель, яка дає змогу визначити чотири вихідних параметрів деякого об’єкта проектування. Значення порахованих вихідних параметрів з використанням розробленої ММ наступні (в безрозмірному вигляді): 10.5, 23.4, 100.1 та 56.7, а значення отримані з допомогою експерименту: 9.3, 25, 112.4 і 49.2.

Визначимо величини відносних похибок для кожного вихідного параметра і загальну похибку побудованої ММ:

, ,

, ,

.

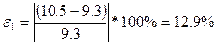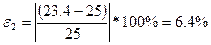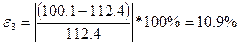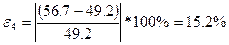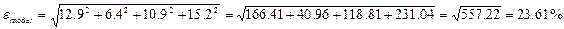Наведений приклад показує, що похибка моделі не може бути меншою за найбільше значення похибки одного з вихідних параметрів математичної моделі.

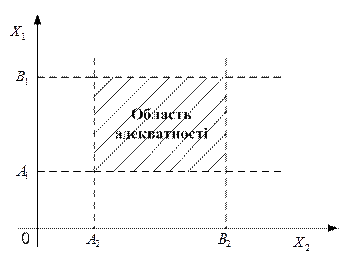
Необхідно зауважити, що точність моделі залежить від умов функціонування об’єкту-оригіналу в просторі зміни вхідних параметрів. В цьому випадку зручніше оперувати поняттям області адекватностімоделі, що визначає область в просторі зміни вихідних параметрів, де виконується умова 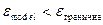( 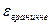–наперед заданеграничне значення похибки ММ).

Рис.2.2. Приклад області адекватності моделі

Слід підкреслити відносний характер наведеного поняття адекватності, тобто прив’язку адекватності моделі до характеристик об’єкту дослідження, які прийнято за основні в рамках цього дослідження. Так, наприклад, якщо вивчається реакція об’єкта на зовнішні збурення того чи іншого класу, то модель, адекватна відносно одного класу збурень, може виявитися неадекватною відносно іншого класу збурень. Іншим характерним прикладом може бути класичне рівняння теплопровідності, отримане на основі закону Фур’є. Це рівняння добре описує еволюцію температури, тобто є адекватним у кількісному відношенні. Крім того, з нього випливає ряд наслідків якісного характеру, які також правильно описують реальний процес поширення тепла: збереження кількості тепла, неможливість концентрації та осциляції температури і т.д. Але з іншої сторони, з цього рівняння випливає також фізично абсурдний висновок про нескінченність швидкості поширення тепла. Таким чином, якщо суттєвою характеристикою процесу вважати швидкість поширення тепла (хоча потреба в цьому виникає досить рідко), то класичне рівняння теплопровідності, як модель реального процесу поширення тепла, стає неадекватним не тільки у кількісному, а й у якісному відношеннях. Для того, щоб отримати модель адекватну і за швидкістю поширення тепла, необхідно уточнити закон Фур’є шляхом врахування інерційності молекул.

Упущення того факту, що адекватність математичної моделі завжди відносна і має свої рамки застосування може привести (і, на жаль, не раз приводило) до спроб нав’язати реальному об’єкту властивості його моделі, наприклад, серйозному сприйнятті твердження, що швидкість поширення тепла є дійсно нескінченною. На жаль, у більш складних випадках, неадекватність моделі виявити набагато складніше, тому застосування неадекватної моделі може привести до того, що можна або не виявити, або занадто спотворити те що насправді є, натомість вивчати те, що нам не потрібно і навіть те, чого взагалі не існує. Як правило у таких випадках перевірка адекватності здійснюється на раціональному рівні, іншими словами “на хлопський розум”, що, безумовно, вступає у конфлікт з чисто дедуктивним (логічним) рівнем і є предметом гострої критики так званих “чистих” математиків. Перевірка адекватності моделі може слугувати також раціональним обґрунтуванням законності застосування прийнятих гіпотез та припущень.

До певної міри протилежною до вимоги адекватності математичної моделі є вимога її достатньої простоти відносно вибраної системи характеристик. Модель є достатньо простою, якщо сучасні засоби дослідження (фізичні, математичні, і зокрема, обчислювальні) дають можливість провести економно, в сенсі затрат праці, але з задовільною точністю кількісний або якісний аналіз вибраних характеристик. Встановлення компромісу між вимогами адекватності та простоти моделі знаходиться на рубежі науки та мистецтва, і в значній мірі залежить від досвіду дослідника. Загальна тенденція полягає в тому, що чим більш адекватною є модель, тим менш простою вона є, хоча досить часто ускладнення моделі може погіршити її адекватність. Іншими словами, спрощення моделі, як правило, знижує її адекватність, хоча є й приклади, коли при спрощенні моделі її адекватність зростає. Можливі також випадки, коли при однаковому ступені простоти вдається побудувати більш адекватну модель, і навпаки, при тій же адекватності – більш просту модель.

Суттєвий вплив на адекватність, і відповідно, на простоту моделі має проблема правильного вибору системи незалежних величин, які достатньо повно характеризують стан об’єкту, який моделюється. Такі величини називаються характеристиками стану, або визначальними параметрами. Логічно припустити, що збільшення кількості визначальних параметрів покращує адекватність моделі. Однак при занадто великій кількості цих параметрів модель може виявитися занадто складною і її дослідження буде дуже ускладнено. З іншого боку, зменшення визначальних параметрів може привести до втрати адекватності моделі.

Важливими параметрами математичних моделей окрім адекватності єуніверсальністьтаекономічність. Універсальність визначається кількістю та складом врахованих в моделі зовнішніх і вихідних параметрів, а економічність характеризується затратами вичислювальних ресурсів для її реалізації. Як правило, на практиці, економічність визначається затратами машинного часу та об’ємом необхідної пам’яті (оперативної та пам’яті на зовнішніх носіях).

Досить часто, в процесі моделювання, оперують поняттям достовірності результатів моделювання, аналізу тощо. Отже достовірність – форма існування (встановлення) істини, яка обгрунтована кількісним способом (наприклад, експериментом, логічним доведенням тощо) для суб’єкта, який пізнає. Процедура оцінки достовірності результатів моделювання називається аналізом адекватності (відповідності) моделі до модельованого об’єкта, системи чи процесу.