Основні параметри методів та алгоритмів

Основними параметрами методів є похибка (точність), економічність, універсальність, надійність та ін.

При переході від математичної моделі до чисельного методу виникають похибки, які називають похибками методу.Вони пов’язані з тим, що будь-який чисельний метод відтворює математичну модель наближено. Найбільш типовими похибками метода є похибка дискретизації і похибки заокруглення.

Як правило застосування чисельного методу для заданої математичної моделі розбивається на два етапи: формулювання дискретної задачі; розробка вичислювального алгоритму, який дасть змогу знайти рішення дискретної задачі.

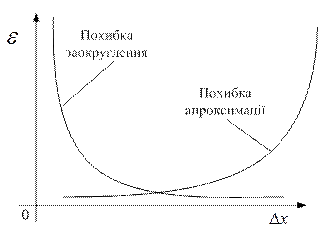
Рис.2.3. Залежності похибок методу від величини кроку дискретизації

Наприклад, якщо початкова математична задача сформульована в вигляді системи диференціальних рівнянь, то для чисельного рішення необхідно замінити її системою досить великої кількості лінійних алгебричних рівнянь. Це відбувається в результаті заміни неперервної області незалежної змінної кінцевою множиною дискретних точок, в яких знаходять рішення. В цьому випадку говорять, що проведена дискретизація початкової математичної задачі. Найпростішим прикладом дискретизації є побудова різницевої схеми шляхом заміни диференціальних виразів скінчено-різницевими аналогами. Зрозуміло, що рішення дискретизованої задачі відрізняється від рішення початкової задачі. Різниця відповідних рішень і називається похибкою дискретизації.

Дискретизована модель являє собою систему великої розмірності алгебраїчних рівнянь. Неможливо знайти рішення такої системи точно в явному вигляді. Тому доводиться використовувати той чи інший чисельний алгоритм рішення системи лінійних алгебраїчних рівнянь. Вхідні дані цієї системи, а саме, коефіцієнти і праві частини задаються в ПК не точно, а з заокругленням. В процесі роботи алгоритму похибки заокруглення, як правило, накопичується, і в результаті рішення, отримане на ПК, буде відрізнятися від точного рішення дискретизованої задачі. Кінцева похибка називається похибкою заокруглення (чи вичислювальною похибкою).

Таким чином, слід розрізняти похибки моделі і методу, реалізуючого дану математичну модель, і при виборі методу (алгоритму) враховувати питання похибки.

Наступним важливим параметром методів є їх економічність. По аналогії з параметром економічності моделей – це є затрати ресурсу персонального компютера (оперативна память та час центрального процесора).

Універсальність методів (алгоритмів) характеризується областю їх застосування. Тобто, чим більша множина задач, які можна розв’язувати з використанням даного методу, тим метод є більш універсальним.

Досить часто важко сформулювати обмеження на застосування того чи іншого методу. Відповідно, можливі ситуації, коли попередньо визначені вимоги застосування методу виконуються, однак задовільне рішення отримати неможливо. Тому, ймовірність вдалого застосування методу менша за одиницю. Отже під надійністю методу (алгоритму) будемо розуміни ймовірність 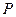правильного отримання результату розв’язання задачі.

В САПР необхідно використовувати надійні методи та алгоритми. Для підвищення надійності методів, досить часто, використовують поєднання різних методів, різного роду настройку методів тощо. Все це робиться для того, щоб добитися значення параметра надійності рівного одиницю чи, хоча б, близького до неї.

Одній і тій же математичній задачі можна поставити у відповідність множину різних дискретних моделей, однак не всі із них придатні для практичної реалізації. Вичислювальні алгоритми, призначені для ПК, повинні задовольняти ряду вимог. Можна виділити дві групи вимог. Перша група пов’язана з адекватністю дискретної моделі вихідної математичної задачі, друга - з реалізацією чисельного методу на ПК.

До першої групи відносяться такі вимоги, як сходимість чисельного методу, виконання дискретних аналогів законів збереження, кількісно правильна поведінка рішення початкової задачі. Пояснимо сказане. Припустимо, що дискретною моделлю задачі є різницева схема, і при заміні диференціальних виразів скінченними різницями отримують велику кількість алгебричних рівнянь. Чим точніше ми хочемо отримати рішення, тим потрібно обрати менший крок сітки, чи параметр дискретизації (x), і тим більшу кількість рівнянь доведеться вирішувати. Говорять, що чисельний метод сходиться, якщо при необмеженому збільшенні кількості рівнянь рішення дискретизованої задачі прагне до точного рішення початкової задачі. Далі, відомо, що диференціальні рівняння математичної фізики є наслідком законів збереження. Тому природно вимагати, щоб для різницевої схеми виконувались аналоги таких законів збереження. Різницеві схеми, які задовольняють цьому методу, називаються консервативними.

Друга група вимог до чисельних методів пов’язана з об’ємом оперативної пам’яті ПК, з можливістю отримати рішення відповідної системи рівнянь за прийнятний час, з стійкістю алгоритму. Алгоритм називається стійким, якщо в процесі рішення ріст вичислювальних похибок обмежений зверху, і нестійким, якщо похибки зростають необмежено. Існують такі алгоритми, які стійкі при виконанні граничних умов для параметрів дискретної моделі. Такі алгоритми називаються умовно-стійкими. Ясно, що використовувати слід стійкі чи умовно стійкі алгоритми.