Основні співвідношення
Наступне співвідношення випливає із теореми Піфагора:
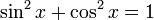
З урахуванням визначення , маємо як наслідок
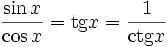

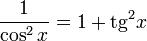
Знаки тригонометричних функцій по четвертях
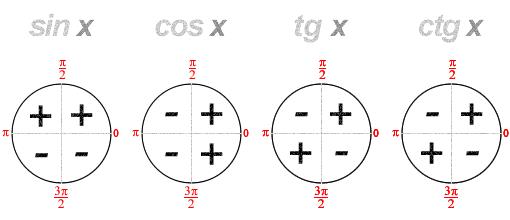
Таблиця значень тригонометричних функцій деяких кутів
| α | 00 | 300 | 450 | 600 | 900 | 1800 |
| 0 рад | π/6 рад | π/4 рад | π/3 рад | π/2 рад | π рад | |
| Sin α | 1/2 | 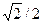
| 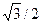
| |||
| cos α | 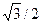
| 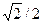
| 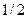
| |||
| tg α | 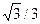
| 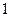
| 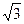
| Не існ. | ||
| ctg α | Не існ. | 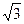
| 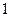
| 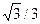
| Не існ. |
Слід пам’ятати:
sin ( - α) = - sin α arcsin ( - α) = - arcsin α
cos ( - α) = cos α arccos ( - α) = π - arccos α
tg ( - α) = - tg α arctg ( - α) = - arctg α
ctg ( - α) = - ctg α arcctg ( - α) = π - arcctg α
sin ( α +2πk) = sin α
cos ( α +2πk) = cos α
tg ( α +πk) = tg α
ctg ( α +πk) = ctg α
Основні формули тригонометрії.
І. ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ СУМИ ДВОХ АРГУМЕНТІВ ( ФОРМУЛИ ДОДАВАННЯ
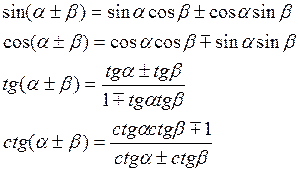
ІІ. ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ ПОДВОЄНОГО АРГУМЕНТА.
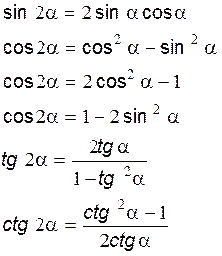
ІІІ. ФОРМУЛИ ЗНИЖЕННЯ СТЕПЕНІ.
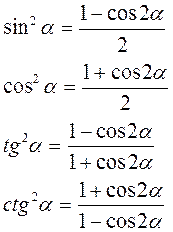
ІV/. ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ ПОЛОВИННОГО АРГУМЕНТА.
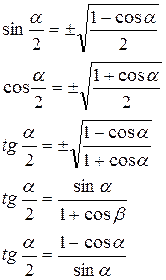
V. ПЕРЕТВОРЕННЯ ДОБУТКУ ТРИГОНОМЕТРИЧНИХ ФУНКЦІЙ НА СУМУ.
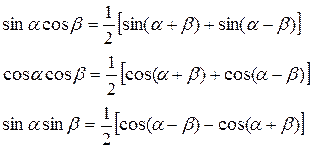
VI. ПЕРЕТВОРЕННЯ СУМИ ТРИГОНОМЕТРИЧНИХ ФУНКЦІЙ НА ДОБУТОК.
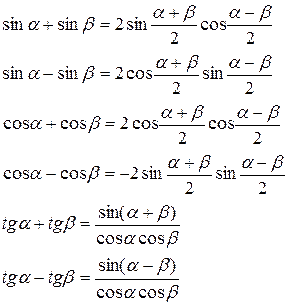

7. «Найпростіші тригонометричні рівняння»
| № п/п | Вид рівняння | Розв’язки | Приклад |
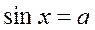
| Якщо 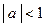 , то , то 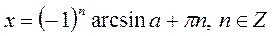 Якщо
Якщо 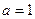 , то , то 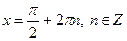 Якщо
Якщо 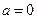 , то , то 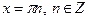 Якщо
Якщо 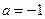 , то , то 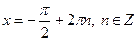
| 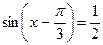
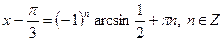 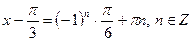
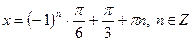
| |
| 2. |
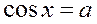
| Якщо 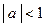 , то , то 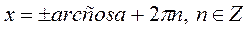 Якщо
Якщо 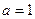 , то , то 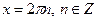 Якщо
Якщо 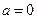 , то , то 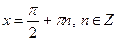 Якщо
Якщо 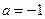 , то , то 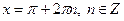
| 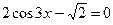 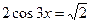
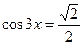
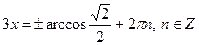
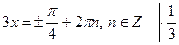
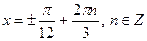
|
| 3. |
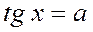
| 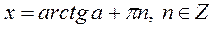 Якщо
Якщо 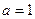 , то , то 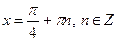 Якщо
Якщо 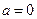 , то , то 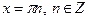 Якщо
Якщо 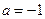 , то , то 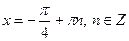
| 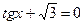
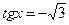
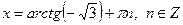
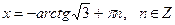 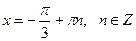
|
| 4. |
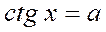
| 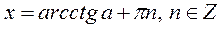 Якщо
Якщо 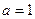 , то , то 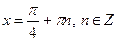 Якщо
Якщо 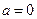 , то , то 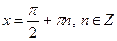 Якщо
Якщо 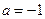 , то , то 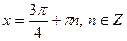
| 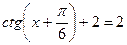 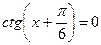 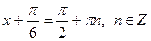
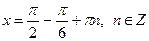
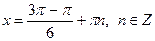
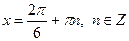
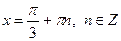
|
Дата добавления: 2016-06-02; просмотров: 1478;
