Дослідження функції на неперервність.
Функція 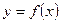 називається неперервною в точці
називається неперервною в точці 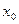 , якщо вона в цій точці визначена і нескінченно малому приросту аргументу відповідає нескінченно малий приріст функції:
, якщо вона в цій точці визначена і нескінченно малому приросту аргументу відповідає нескінченно малий приріст функції: 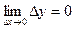 .
.
Функція 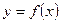 називається неперервною в точці
називається неперервною в точці 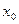 ,якщо виконуються слідуючи умови:
,якщо виконуються слідуючи умови:
1) функція визначена в точці 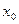 ;
;
2) існує границя функції в точці 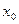 ;
;
3) значення функції в точці 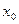 співпадає із значенням границі в точці
співпадає із значенням границі в точці 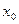 .
.
Число А називається границею функції 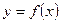 справа при
справа при 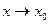 ,
, 
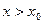 , якщо функція визначена у правому
, якщо функція визначена у правому 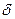 - околі точки
- околі точки 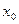 , і для будь – якого
, і для будь – якого 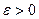 знайдеться таке
знайдеться таке 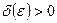 , що для всіх
, що для всіх 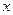 , взятих з інтервалу
, взятих з інтервалу 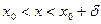 виконується нерівність
виконується нерівність 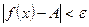 .
.
Позначають 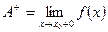
Число А називається границею функції 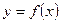 зліва при
зліва при 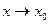 ,
, 
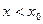 , якщо функція визначена у лівому
, якщо функція визначена у лівому 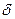 - околі точки
- околі точки 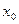 , і для будь – якого
, і для будь – якого 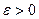 знайдеться таке
знайдеться таке 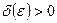 , що для всіх
, що для всіх 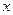 , взятих з інтервалу
, взятих з інтервалу 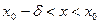 виконується нерівність
виконується нерівність 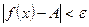 .
.
Позначають 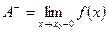
Функція 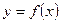 називається неперервною в точці
називається неперервною в точці 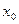 ,якщо виконуються слідуючи умови:
,якщо виконуються слідуючи умови:
1) функція визначена в точці 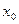 і в деякому околі цієї точки;
і в деякому околі цієї точки;
2) існують односторонні границі 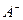 і
і 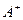 ;
;
3) односторонні границі рівні між собою і дорівнюють значенню функції в точці 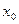 .
.
Дата добавления: 2016-06-02; просмотров: 2226;
