Елементарні функції та їх графіки
ФУНКЦІЇ, ЇХ ВЛАСТИВОСТІ ТА ГРАФІКИ
1. Функцією називається відповідність між двома множинами, при якій кожному елементу однієї множини ( області визначення ) відповідає єдиний елемент іншої множини ( області значень ).
Область визначення функції має обмеження у таких випадках:
· 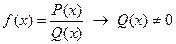
· 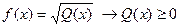
· 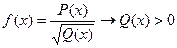
1. Функція зростає, якщо більшому значенню аргумента відповідає більше значення функції і спадає в іншому випадку:
f(x) ↑↔ x2>x1→ f(x2)>f(x1);
f(x) ↓↔ x2>x1→ f(x2)<f(x1);
Функція парна, якщо при зміні значення аргументу на протилежне значення функції не змінюється: f (-x) =f(x).
Функція непарна, якщо при зміні значення аргументу на протилежне значення функції змінюється на протилежне: f (-x) = - f(x).
Функція, що не являється непарною та парною називається функцією загального вигляду.
Елементарні функції та їх графіки
| № п/п | Назва функції. | Формула. | Графік. | |||
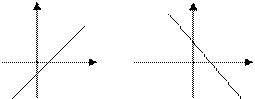
| 1. | Лінійна функція |
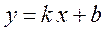
| Пряма лінія.
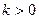 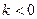
| |||
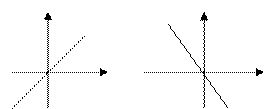
| 2. | Пряма пропорційність. |
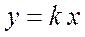
| Пряма лінія, що проходить через початок координат.
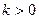 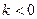
| |||
| 3. | Обернена пропорційність. |
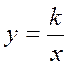
| Гіпербола.
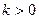 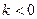
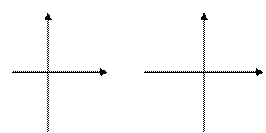
| |||
| 4. |
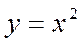
|  Парабола. Парабола.

| ||||
| 5. |
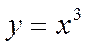
|  Кубічна парабола. Кубічна парабола. 
| ||||
| 6. |
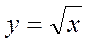
| «Лежача» вітка параболи

| ||||
| 7. |
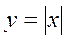
| 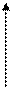 Кут, утворений бісектрисами 1 та 2 чверті. Кут, утворений бісектрисами 1 та 2 чверті.
|
4. Найпростіші перетворення графіків функцій.
| № п/п | Функція | Перетворення. |
| | 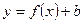
| Одержується з графіка функції 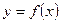 зміщенням вздовж осі Оу вгору на зміщенням вздовж осі Оу вгору на 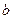 одиниць, якщо одиниць, якщо 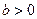 ; вниз, якщо ; вниз, якщо 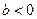 . .
|
| | 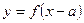
| Одержується з графіка функції 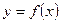 зміщенням вздовж осі Ох вправо на зміщенням вздовж осі Ох вправо на 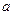 одиниць, якщо одиниць, якщо 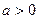 ; вліво, якщо ; вліво, якщо 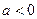 . .
|
| | 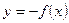
| Одержується симетричним відображенням графіка функції 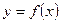 відносно осі Ох. відносно осі Ох.
|
| | 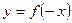
| Одержується симетричним відображенням графіка функції 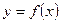 відносно осі Оу. відносно осі Оу.
|
| | 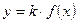 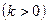
| Одержується з графіка функції 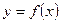 розтягненням вздовж осі Оу в розтягненням вздовж осі Оу в 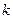 разів, якщо разів, якщо 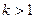 ; або стисненням до осі Ох, якщо ; або стисненням до осі Ох, якщо 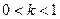 . .
|
| | 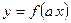 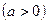
| Має той самий вигляд, що й у графіка 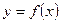 , тільки розтягнено від осі Ох, якщо , тільки розтягнено від осі Ох, якщо 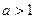 , або стиснено до осі Ох, якщо , або стиснено до осі Ох, якщо 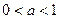 . .
|
| | 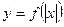
| Ділянки графіка 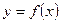 , які лежать праворуч від осі Оу – без зміни, і ця ж сама частина симетрично відображається відносно осі Оу. , які лежать праворуч від осі Оу – без зміни, і ця ж сама частина симетрично відображається відносно осі Оу.
|
| | 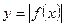
| Ділянки графіка 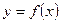 , які лежать вище від осі Ох – без зміни, а та частина, що нижче від осі Ох - симетрично відображається відносно осі Ох. , які лежать вище від осі Ох – без зміни, а та частина, що нижче від осі Ох - симетрично відображається відносно осі Ох.
|
| | 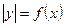
| Ділянки графіка 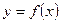 , які лежать вище від осі Ох – без зміни, і ця ж сама частина симетрично відображається відносно осі Ох. , які лежать вище від осі Ох – без зміни, і ця ж сама частина симетрично відображається відносно осі Ох.
|
Дата добавления: 2016-06-02; просмотров: 7107;


