Тема 6. Динамическое программирование как инструмент принятия управленческих решений

1. Специфика динамического программирования.

2. Динамическая оптимизационная модель управления запасами.

3. Модель замены оборудования в виде марковских цепей.

1. Динамическое программирование является разновидностью подхода оптимизации. Оно обладает той специфической особенностью, что решение оптимизационной задачи можно свести к решению более простых «подзадач» с увязкой этих решений при использовании специальных соотношений. В результате вопрос о глобальной оптимизации некоторой функции сводится к поэтапной оптимизации некоторых промежуточных целевых функций. В силу этого задача динамического программирования (ДП) заключается в многошаговой оптимизации по получению общего (результирующего) оптимума (максимума или минимума).

Начало развития динамического программирования относится к 50-м годам XX века и связано с именем американского математика Р. Беллмана. Ему принадлежит разработка основного функционального уравнения, которое является математическим выражением сформулированного им же одного из важнейших принципов ДП – принципа оптимальности. Этот принцип состоит в следующем: оптимальное поведение обладает тем свойством, что, каковы бы ни были первоначальное состояние и решение в начальный момент, последующие решения должны составлять оптимальное поведение относительно состояние, получающегося в результате первого решения (оптимальное поведение – последовательное улучшение чего-либо). Динамическое программирование отличается от других разделов математического программирования тем, что первоначальные варианты на момент решения задачи ДП уже известны. Особенностью модели ДП является то, что увеличение количества переменных в задачах вызывает рост возможных вариантов решения. Возникает так называемая проблема размерности (или «принятие размерности» по выражению Р. Беллмана), которая является серьезным препятствием при решении задач ДП средней и бальной размерности даже на ПК (из-за ограниченности объема оперативной памяти).

Методом ДП решается большой спектр экономических задач в экономической практике на микроуровне народного хозяйства: задачи оптимального распределения капиталовложений между возможными новыми направлениями их использования; замены выбывающих из эксплуатации основных фондов; составления календарных планов текущего, среднего и капитального ремонта сложного оборудования; оперативно-календарного планирования производства продукции; выравнивания занятости сотрудников в условиях колеблющегося спроса на продукцию; управления запасами, устанавливающими момент пополнения запасов и размер пополняющего заказа.

Целевая функция ДП является аддитивной от показателей эффективности каждого шага (аддитивная функция – функция, значение которой определяется как сумма значений частных показателей). При этом исходят из того, что состояние S_k системы в конце k-ого шага зависит только от предшествующего состояния S_k-1 и управления на k-м шаге х_k (и не зависит от других предшествующих состояний и управлений). Это требование называется «отсутствием последствия».

Обозначим показатель эффективности k-ого шага через

Z_k = f_k(S_k-1,x_k), k=1,2,…n (32)

Тогда

Z = 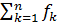(S_k-1,x_k) (33)

Таким образом, особенности модели ДП

1. Задача оптимизации интерпретируется как n-шаговый процесс управления.

2. Целевая функция равна сумме целевых функций каждого шага.

3. Выбор управления на k-м шаге зависит только от состояния системы к этому шагу, не влияет на предшествующие шаги (нет обратной связи).

4. Состояние S_k после k-ого шага управления зависит только от предшествующего состояния S_k-1 и управления х_k (отсутствие последствия).

5. На каждом шаге управление x_k зависит от конечного числа управляющих переменных, а состояние S_k – от конечного числа параметров. Например, в задаче о распределении инвестиций между предприятиями холдинга в качестве x_k выступает количество средств, выделяемых k-ому предприятию. Функцией f_k прибыль или прирост выпуска продукции. На первом этапе планирования доходы (прирост доходов) холдинга будут соответствовать приросту выпуска продукции на каждом предприятии. Далее будет использоваться функциональное уравнение Беллмана:

F_n (x) = max (f(y)+ g (x-1) + F_n-1 [ay+b(x-y)]), (34)

0≤y≤x

где х – объем инвестиций;

y – объем инвестиций, выделенных первому предприятию;

(х-у) – объем инвестиций, выделенных второму предприятию;

F(y) и g(x-y) – известные функции распределения доходов (прироста выпуска);

а, b – параметры, выражающие капиталоотдачу.

Так как на первом этапе планирования никаких расчетов по формуле Беллмана не производится, а затем идет попарное сравнение результатов инвестирования (на втором шаге – результаты инвестирования в первое и/или второе предприятие; на третьем шаге – от результата инвестирование во второе и/или третье; на четвертом шаге – результаты инвестирования в третье и/или четвертое предприятие), то число шагов (этапов) планирования совпадает с числом предприятий. Выбор переменных х₁,х₂,х₃,х₄ – управление соответственно на I, II, III и IV шагах. Перебор вариантов и формирование этапов планирования может осуществляться и по числу. На 1 шаге последовательно (рекуррентно) наращивают инвестиции в 1 предприятие, а остаток инвестиций распределяется между оставшимися. На 2 шаге – роль 1 предприятия (которому в первую очередь выделяют инвестиции) выполняет 2 предприятие; на 3 шаге – 3 предприятие; на 4 шаге – 4 предприятие.

Пример. Имеется 4 предприятия холдинга, выпускающие однородную продукцию. Рассматриваются планы реконструкции и модернизации каждого из предприятий при общем объеме капиталовложений х₀ = 400 тыс. д.е. Он должен быть распределен между предприятиями таким образом, чтобы максимизировать общий прирост выпуска продукции холдинга. В таблице приведены данные объемов реконструкций по этапам планирования (у) и прироста выпуска продукции по каждому предприятию f_i(y) при i=1…4.

Таблица