Тема 7. Классическая схема принятия управленческих решений в условиях риска и неопределенности

1. Риск как измеримая неопределенность.

2. Байессовский подход к принятию решений.

3. Методы оценки и регулирования рисков.

4. Показатели и шкалы риска.

5. Компромисс между риском и прибылью.

6. Инструменты и приемы разработки и выбора управленческих решений в условиях полной неопределенности.

1. Риск характеризуется как неопределенность, связанная с возможностью в ходе реализации решения (проекта) неблагоприятных ситуаций и последствий. Американский ученый Ф. Найт отмечал, что измеримая неопределенность (или собственно риск) настолько отличается от неизмеримой, что по существу вообще не является неопределенностью.

Риск нельзя смешивать с шансом – возможным успехом (см. формулу 38)

P_r + P_c = 1 (38)

где P_r - вероятность риска (неблагоприятного исхода) деятельности;

P_c – вероятность шанса (благоприятного исхода) деятельности.

В то же время и риск, и шанс нельзя сводить к вероятности наступления соответствующих событий. Риск определяется и величиной отрицательного экономического результата (убытка, ущербом, упущенной выгодой).

Вероятность рискового события может быть подразделена на объективную (априорную и апостериорную) и субъективную. Априорная объективная вероятность устанавливается на основе знания устойчивых зависимостей, соотношений. Априорная вероятность определяется на основе обработки данных статических наблюдений. Априорная объективная вероятность может быть рассчитана для узкого круга событий (например, в азартных играх). При большом числе испытаний (наблюдений) частота событий является апостериорной объективной статистической вероятностью.

Говорят, что событие А имеет вероятность, если это событие обладает следующими особенностями:

- можно, по крайней мере принципиально, провести в неизменных условиях неограниченное число независимых друг от друга испытаний, в каждом из которых может появиться или не появиться событие А;

- в результате достаточно многочисленных испытаний замечено, что частота события А почти для каждой большой группы испытаний лишь незначительно отклоняется от некоторой постоянной.

Определение статистической (апостериорной) вероятности предполагает наличие неизменных условий деятельности и ограничено возможностью достичь полной однородности сгруппированных случаев. При отсутствии аналогичного опыта в прошлом в связи с изменением цели решения, ситуации его принятия и условий реализации необходимо использование субъективной вероятности. Субъективная вероятность является предположением относительного определенного результата. Это предположение основывается на суждении и личности оценивающего.

Следует различать риск, возникающий в результате выбора и реализации решения, риск как неотъемлемый элемент человеческой деятельности (не только предпринимательской). Используется специальный термин «деятельностный риск». Такое разграничение важно для оценки и регулирования рисков, но у обоих типов риска единая сущность – опасность негативных последствий.

Управленческие риски – опасность негативных последствий в процессе принятия и реализации управленческих решений вследствие ошибочного прогноза развития (состояния) внешней среды, неадекватного формулирования целей и средств решения деловых проблем предприятия (организации), ошибок в процессе обоснования и реализации выбранных альтернативных вариантов функционирования и развития экономических систем.

2. В процесс управления предприятиями и организациями часто возникает необходимость и возможность корректировки ранее принятых решений с учетом новой информации, появившейся в том числе в результате экспериментирования. Например, предприниматель предполагает осуществлять поставку на риск нового перспективного товара, но он не знает, «пойдет» ли товар. Для уточнения ситуации он производит пробную партию и смотрит как она раскупается. После этого ситуация становится более определенной и прогнозируемой.

В этих ситуациях для принятия окончательного решения применяется байессовский подход, который выглядит следующим образом. Известно, что событие А произошло. В результате пробной операции требуется найти вероятность того, что событие А (например, успешный выход нового товара на рынок) произойдет. 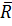До проведения пробной операции был разработан прогноз реализации нового товара, а на основе этого прогноза можно найти средний ожидаемый доход и средний ожидаемый риск (см. формулы 39 и 40)

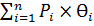= (39)

где 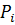- вероятность полной, частичной или нулевой реализации нового товара;

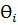– объем продаж при полной, частичной или нулевой реализации нового товара.

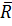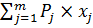= (40)

Где 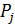– вероятность возникновения потерь определенной величины вследствие частичной или нулевой реализации нового товара;

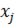– размер потерь при данном j-ом негативном результате по продаже нового товара.

После проведения пробной операции (реализации новой партии нового товара) для оценки вероятности реализации нового товара в полном объеме используется формула Байеса (см. формулу 41)

P(H_k│A) = 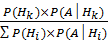, (41)

где 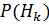- вероятность реализации нового товара по первоначальному прогнозу;

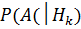– вероятность реализации нового товара после успешной продажи пробной партии;

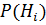– вероятность продажи нового товара при успешной и неуспешной реализации пробной партии;

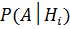– вероятности реализации нового товара после успешной или неуспешной реализации нового товара.

Пример. Предприятие рассматривает вопрос о выпуске нового товара и его выводе на рынок. Вероятность успеха оценивается в 0,5. Проводится рекламная распродажа. Если рекламная распродажа будет успешной, то в 70% случаев товар конкурентоспособен. Если рекламная распродажа будет неудачной, то в 20% случаев товар конкурентоспособен. Рекламная распродажа оказалась успешной. Определить вероятность успешного выхода нового товара на рынок.

Решение.

Р = 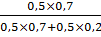= = 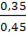0,78

Вероятность успешного вывода нового товара на рынок – 78 процентов.

На основе формулы Байеса определяется целесообразность и пробных операций. Считается, что пробная операция оправдана, если расходы на ее проведение меньше увеличения среднего ожидаемого дохода, рассчитанного по уточненным вероятностям.

3. О методах оценки и регулирования рисков подробно можно посмотреть в учебном пособии А.С. Лифшица «Управленческие решения» (М.: Кнорус, 2009).

4. К показателям риска следует отнести точку безубыточности и кромку безопасности, внутреннюю норму доходности, меру риска, степень риска, коэффициенты вариации (см. Лифшиц А.С. Управленческие решения. М.; 2009. С. 193-197, 240). При этом следует иметь в виду, что минимизация средних потерь предоставляется вполне естественной, если все возможные потери малы по сравнению с ресурсами предприятия. Может использоваться максимизация математического ожидания функции полезности (в случае, когда полезность денежной единицы меняется в зависимости от общей располагаемой суммы, например, когда необходимо исключить возможность разорения собственника). Построение математической функции полезности требует организации специального эконометрического исследования.

При оценке риска могут использоваться шкала Харрингтона (Лифшиц, 2009, С.167), шкала допустимого риска (Лифшиц, 2009, С.196), зоны риска (Лифшиц, 2009, С.195).

5. В экономической теории аксиомой считается положение о том, что стремление предпринимателя получить большую прибыль влечет за собой увеличение абсолютного риска (который измеряется средним квадратичным отклонением) и относительного риска (который измеряется коэффициентом вариации). По мере повышения риска требуемая прибыль также увеличивается, но не так быстро.

Существуют специальные кривые, которые представляют функции риска – прибылей. Покажем их использование на условном примере. Пусть имеется 3 варианта, при реализации которых значения математического ожидания прибыли равны соответственно 15,15 и 10 д.е., а коэффициент вариации 33, 100 и 0 процентов. Кривые функции риск-прибыль также называются кривыми безразличия (отражают соответствие риска и прибыли, каждая точка на кривой - смесь из уровня риска и прибыли). Если лицо не принимает риск (точнее считает, что максимальному риску должен соответствовать максимальный уровень прибыли, существенно превышающий значение 15 д.е.), то вариант 2 будет однозначно отвергнут. Лицо, с предельными требования к соотношению риск-прибыль, может выбрать вариант 1, предпочтя его варианту 3, если даже вариант 3 свободен от риска, потому что предполагаемая прибыль по 1 варианту выше, чем прибыль, которая ему требуется после должного учета риска (например, 13 д.е. прибыли при коэффициенте вариации 33 процента). Лицо, с умеренными требованиями к соотношению риск-прибыль (т.н. лица, подвергающееся риску), может рассмотреть все 3 приемлемые для него варианта, но оно, скорей всего, выберет 1 вариант, потому что он обещает наибольшую прибыль (второй вариант выше кривой безразличия для данного лица, но в меньшей степени, чем первый).

Два широко известных ученых – Леилтон Фридман и Леонард Дж. Сэйдвидж были обеспокоены традиционным подходом, основанном на предельной полезности, потому что он не объясняет, почему человек может одновременно демонстрировать принятие на себя риска и стремление избежать риска. Например, человек, который играет (первый тип поведения), с большей вероятностью поедет в казино на застрахованном автомобиле и будет жить в застрахованном доме (второй тип поведения). Фридман и Сэйвидж пытались объяснить такое поведение гипотезами функции полезности, которая вначале растет, а затем стабилизируется и падает. Отношение инвестора к риску зависит прежде всего от формы кривой полезности, которая в свою очередь зависит от личности инвестора, а затем от текущего положения каждой кривой, которая определяется текущим доходом. Если текущий доход низок, то предельная полезность дохода (полезность приращения дохода на единицу) высока, и человек готов согласиться на риск при меньшей премии, чем в том случае, когда доход высок. Или, как утверждает гипотеза Фридмана – Сэйвиджа, на низких уровнях дохода человек даже может искать риск.

Вопрос – но ведь богатый человек поехал в казино? А с другой стороны, есть русская поговорка – «Чем богаче, тем жаднее»? И ведь считается, что мужчина, лица с опытом и более высоким доходом склонны принимать более рискованные решения? Все ли объясняет в плане рискового поведения гипотеза Фридмана-Сэйвиджа?

6. Важным инструментом принятия решений в условии неопределенности является имитационное моделирование. Имитационное моделирование должным образом учитывает случайный (стохастический) характер воздействия на экономические системы объективных и субъективных факторов. Имитационное моделирование – пошаговое моделирование, при этом шагом является промежуток между 2 последующими «особыми состояниями». В это время состояние имитируемой системы неизменно. Одной из имитационных моделей, разработанных в Ивановском госуниверситете является имитационная модель ткацкого участка. Более подробно об особенностях имитационного моделирования и особенностях имитационной модели ткацкого участка можно посмотреть в учебном пособии Е.Н. Гинзбурга, М.А. Вортман и Е.П. Патрушевой (Иваново, 1985).

Критериями (методологическими приемами) принятия решений в условиях неопределенности являются критерий Лапласа; критерий решения Вальда, называемой также максимином (критерий пессимизма); критерий макси-макса (критерий оптимизма); альфа-критерий решения Гурвица; критерий решения Сэвиджа – минимизация максимума возможного сожаления (упущенной выгоды). Формулы расчета критериальных значений и пример такого расчета см. Лифшиц А.С. Управленческие решения (Москва,2009). Наиболее объективным критерием представляется критерий Сэвиджа, избегающий неизбежно в известной мере субъективных коэффициентов оптимизма (как в критерии Гурвица), крайних оценок (максимин, максимакс) или усреднения при нереальной равновероятности событий (Лаплас).