Тема 9. Методы и модели теории массового обслуживания и практические аспекты их применения

1. Основные понятия теории массового обслуживания (ТМО).

2. Классификация и качества функционирования системы массового обслуживания

3. Марковский случайный процесс, простейший поток требований и количественное описание времени обслуживания. Методические особенности статистического моделирование систем массового обслуживания (метод Монте-Карло).

1. При исследовании операций часто приходится сталкиваться с системами, предназначенными для многоразового использования при решении однотипных задач. Возникающие при этом процессы получили название процессов обслуживания, а системы – систем массового обслуживания. Примерами таких систем являются телефонные станции, ремонтные мастерские, вычислительные комплексы, билетные кассы, магазины, парикмахерские и т.п.

Каждая система массового обслуживания (СМО) состоит из определенного числа обслуживающих единиц (приборов, устройств, пунктов, станций), которые называются каналами обслуживания. Каналами могут быть линии связи, рабочие точки, вычислительные машины, продавцы. По числу каналов СМО подразделяют на одноканальные и многоканальные.

Заявки поступают в СМО обычно не регулярно. А случайно, образуя т.н. случайный поток заявок (требований). Обслуживание заявок продолжается какое-то время. Случайный характер потока заявок и времени обслуживания приводит к тому, что СМО оказывается загруженной неравномерно: в какие-то периоды времени скапливается очень большое заявок (они либо становятся в очередь, либо покидают СМО необслуженными), в другие же периоды СМО работает с недогрузкой или простаивает.

Предметом теории массового обслуживания является построение математических моделей, связывающих заданные условия работы СМО (число каналов, их производительность, характер потока заявок и т.п.) с показателями эффективности СМО, описывающими ее способность справляться с потоком заявок.

2. СМО делят на два основных типа: СМО с отказами и СМО с ожиданием (очередью). Пример СМО с отказами (заявка на телефонный разговор в момент, когда все каналы заняты, получает отказ и покидает СМО необслуженной). В СМО с ожиданием заявка, пришедшая в момент, когда все каналы заняты, не уходят, а становятся в очередь на обслуживание. СМО с ожиданием подразделяют на виды, в зависимости от того, как организована очередь: с ограниченной или неограниченной длиной очереди, с ограниченным временем ожидания и т.п.

Для классификации СМО важное значение имеет дисциплина обслуживания, определяющая порядок выбора заявок из числа поступивших и порядок распределения их между свободными каналами. По этому признаку обслуживания заявок может быть организовано по принципу «первая пришла – первая обслужена», «последняя пришла – первая обслужена» (такой порядок, может применяться, например, при извлечении для обслуживания изделий со склада, ибо последние из них часто оказываются более доступными; должны учитываться и экономические соображения) или обслуживание с приоритетом (когда в первую очередь обслуживаются наиболее важные заявки). Приоритет может быть как абсолютным, когда более важная заявка «вытесняет» из-под обслуживания обычную заявку (например, в случае аварийной ситуации плановые работы ремонтных бригад прерываются до ликвидации аварии), так и относительным, когда более важная заявка получается лишь «лучшее» место в очереди.

Качество функционирования СМО – степень удовлетворения потребности в обслуживании (при этом низкое качество обслуживания может считаться равносильным неудовлетворению требования). Например, если методами ТМО исследуется работа дежурных слесарей-ремонтников, то под качеством их работы прежде всего понимается не качество ремонта вышедшего из строя оборудования (хотя это очень важно), а такие показатели, как, величина очереди оборудования, ожидающего ремонта; среднее время, в течение которого оборудование ремонтируется и ожидает ремонта (время нахождения требования в обслуживающей системе); время простоя дежурных слесарей.

При оценке качества функционирования СМО могут использоваться и такие показатели как среднее число заявок, обслуживаемых в единицу времени; вероятность отказа в обслуживании без ожидания; вероятность того, что число заявок в очереди превысит определенное значение. Выбор показателей качества функционирования СМО определяется особенностями конкретных систем.

3. Процесс работы СМО представляет собой случайный процесс. Под случайным (вероятностным или стохастическим) процессом понимается процесс изменения во времени состояния какой-либо системы в соответствии с вероятностными закономерностями.

Процесс работы СМО представляет собой случайный процесс с непрерывным временем. Это означает, что состояние СМО меняется скачком в случайные моменты появления каких-то событий (например, приход новой заявки, окончания обслуживания).

Математический анализ работы СМО существенно упрощается, если процесс этой работы марковский. Случайный процесс называется марковским или случайным процессом без последствия, если для любого момента времени t₀ вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент t₀ и не зависят от того, когда и как система пришла в это состояние.

Под потоком событий понимается последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени (например, поток вызовов на телефонной станции, поток покупателей и т.п.). Поток характеризуется интенсивностью – частотой, появление событий или средним числом событий, поступающих в СМО в единицу времени. Поток событий называется регулярным, если события следуют одно за другим через определенные промежутки времени. Пример – поток изделий на конвейере (с постоянной скоростью движения). Поток событий называется стационарным, если его вероятностные характеристики не зависят от времени. Например, поток автомобилей на городком проспекте не является стационарным, но этот поток можно считать стационарным в определенный период суток, скажем, в часы пик. В последнем случае фактическое число автомобилей, проходящих в единицу времени (например, в каждую минуту) может заметно отличаться друг от друга, но среднее их число постоянно и не будет зависеть от времени.

Поток событий называется потоком без последействия, если для любых двух непересекающихся участков времени τ₁ и τ₂. Число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие. Например, поток пассажиров, входящих в метро практически не имеет последствия. А, скажем, поток покупателей, отходящих с покупками от прилавка, уже имеет последствия (хотя бы потому, что интервал времени между отдельными покупателям не может быть меньше, чем минимальное время обслуживания каждого из них).

Поток событий называется ординарным, если вероятность попадания на малый (элементарный) участок времени ∆t двух и более событий пренебрежимо мала по сравнению с вероятностью попадания одного события. Поток ординарен, если события появляются в нем поодиночке, а не группами. Например, поток поездов, подходящих к станции, ординарен, а поток вагонов не ординарен.

Поток событий называется простейшим (или стационарным пуассоновским), если он одновременно стационарен, ординарен и не имеет последствия. Название «простейший» объясняется тем, что СМО с простейшими потоками имеет наиболее простое математическое описание. Регулярный поток не является «простейшим», т.к. он имеет последствие: моменты появления событий в таком потоке жестко зафиксированы. Математически доказано, что если поток требований простейший, то зная его параметры, математическое ожидание числа требований, поступающих в систему в единицу времени, его можно полностью описать количественно с помощью функций Пуассона:

P_k(t) = 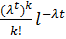, (k = 0,1,2…), (42)

P_k(t) – вероятность того, что в течение времени о-t в систему поступит точно k требований на обслуживание;

λ – параметр потока – среднее число требований, поступающих в единицу времени;

l – основание натуральных логарифмов (l = 2,71828)

Изменяя значения k и t, по приведенной формуле можно рассчитать вероятность любого состояния потока требований. Кроме того, по рассчитанным вероятностям отдельных событий можно определить также накопленные вероятности:

вероятность того, что в систему поступит требований не больше какого-то наперед заданного числа k:

P (k ≤ K) = 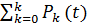(43)

и вероятность того, что число требований, поступающих в систему в течение времени о-t, будет больше заданного числа k:

P (k>K) = 1-Р(K) =l 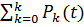(44)

Существуют особенности определения эффективности СМО с отказами (одноканальной и многоканальной), СМО с ожиданием (очередью – ограниченной и неограниченной). Подробно можно посмотреть в Исследование операций в экономике: учеб. пособие (под ред. Н. Ш. Кремера. 2-е изд., переоб. и доп. М., 2010. С.375-395).

Основное допущение, при котором анализируются СМО, состоит в том, что все потоки событий, переводящие их из состояния в состояние, были простейшие. При нарушении этого требования общих аналитических методов для таких систем не существует. В случаях, когда для анализа работ СМО аналитические методы не применимы, используют универсальный метод статистического моделирования или, как его называют метод Монте-Карло. Идея метода Монте-Карло – проведение «розыгрыша» случайного процесса с помощью специально организованной процедуры. В результате такого «розыгрыша» получается каждый раз новая реализация случайного процесса. Это множество реализаций можно использовать как искусственный статистический материал. После обработки которого могут быть получены приближенно любые характеристики обслуживания. Например, необходимо проанализировать очереди, возникающие в магазине, для решения вопроса о расширении магазина.

Время подхода покупателей и время их обслуживания несет случайный характер, и их распределения могут быть установлены по имеющейся информации. В результате взаимодействия этих случайных процессов создается очередь. Согласно методу Монте-Карло перебирают (с помощью ЭВМ) все возможные состояния системы с различным числом покупателей, времени обслуживания, сохраняя такие же характеристики распределения.