Тема 5. Теория графов и оптимизация управленческих решений

1. Предмет, значения и основные понятия теории графов.

2. Правила построения и оптимизации сетевых графиков.

1. Создание сложной техники и крупных объектов (например, самолетов, судов, автомобилей, строительных сооружений) требует объединения усилий нескольких коллективов: проектных и научно-исследовательских учреждений, предприятий. Чтобы завершить создание сложной техники или объектов к определенному сроку, необходимо увязать выполнение работ всеми исполнителями по времени, стоимости, ресурсам, другим технико-экономическим показателям. Такая увязка обеспечивается методами сетевого планирования и управления (СПУ). СПУ базируется не теории графов.

Теория графов – область дискретной математики, предметом исследования которой являются структуры, состоящие из точек (вершин графа) и соединяющих их произвольным образом линий со стрелками (дух графа), либо линий без стрелок (ребер графа).

Граф – совокупность точек (вершин) и линий (ребер), соединяющих некоторые пары этих точек. Некоторые ребра графа снабжены стрелками. Их называют ориентированными ребрами или дугами.

Формой графа является сетевая модель.

Сетевая модель – план выполнения некоторого комплекса взаимосвязанных работ, заданного в специфической форме сети, графическое изображение которой называется сетевым графиком. Отличительной особенностью сетевой модели является четкое определение всех временных взаимосвязей предстоящих работ.

Главными элементами сетевой модели являются события и работы.

Термин работа – любые протяженные во времени действия, которые приводят к достижению определенных результатов. Работы соответствуют дугам графа. События – моменты – момент завершения работы. Они соответствуют вершинам графа. В сетевом графике могут быть несколько разновидностей работ: действительная работа, ожидание, фиктивная работа. Действительной называется работа, требующая затрат времени и ресурсов: например, изготовление узла машины, составление программы для персонального компьютера и т.д. Ожиданием называется работа, которая требует затрат времени, но не требует затрат ресурсов: например, процесс затвердевания бетона; созревания урожая; сушка после покраски. Фиктивная работа отражает логическую связь между работами и не требует затрат времени и ресурсов. Она указывает, что возможность начала одной работы непосредственно зависит от результатов другой: например, передача чертежей из конструкторского бюро в цех для изготовления деталей, передача программы для ПК оператору с целью ввода ее в оперативную память и последующей отладки.

Действительные работы и ожидания изображаются на графике сплошными линиями, фиктивная работа – пунктирными.

События соответствуют результатам произведенной работы: штамп изготовлен, узел спроектирован, программа для ПК отлажена.

Событие представляет собой только момент совершения работы (работ) и может быть только отправным моментом для начала последующих работ. События изображают кружками, внутри кружка – номер события (см. рис.1).

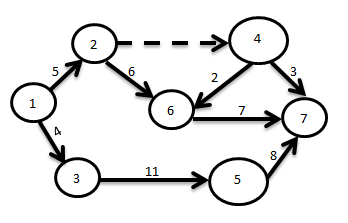
Рис.1. Элементы сетевого графика

Различают предшествующие данной работе события i (например, для работ «составление программы» предшествующим событием может являться «схема алгоритма расчета составлена») и последующие за данной работой события (например, для работ «составления программы» последующим событием является «программа составлена»). На рис.1 примером предшествующего события может быть событие 3, а последующим событие 5. Работа между событиями i и j обозначается как (i,j).

Первоначальное событие в сети, отражающее начало определенного комплекса и не имеющее входящих в него работ называется исходным I (событие 1 на рис.1). Событие, отражающее конечную цель определенного комплекса работ и не имеющее выходящих из него работ, называется завершающим С (событие 7 на рис.1).

Последовательность работ, приводящая от одного события к другому в которой каждая работа встречается не более одного раза, составляет путь. Может быть несколько полных путей от исходного события I до завершения события С. Полный путь, имеющий наибольшую продолжительность, называется критическим. Кроме того, используются понятия пути, предшествующего данному событию i – от исходного (1) до данного события i, а также пути, последующего за данным событием i – от данного i до завершения события С.

2. При построении сетевого графика необходимо соблюдать ряд правил.

1. График строится слева направо, от исходного события к завершающему.

2. Длина и наклон стрелок, с помощью которых изображаются работы в сети, значения не имеют. Однако все они должны иметь одно направление – слева направо, от предшествующего события к последующему.

3.На графике не должно быть контуров, т.е. замкнутых путей, которые соединяют события с ними же самими.

4. Пара событий не может быть соединена более чем одной работой, т.е. сетевой график не может быть мультиграфом. Для устранения этой ситуации вводится дополнительное событие (например, 2') и фиктивная работа (пунктир). Фиктивная работа может следовать до и после действительной работы.

5. В сети не может быть хвостовых событий (кроме исходного), т.е. событий, в которые не входит ни одна работа.

6. На графике не может быть тупиковых событий (кроме завершающих): например, чтобы из события i не выходила ни одна работа.

7. Сетевой график – это плоский граф. Граф называется плоским, если его можно изобразить на плоскости так, что все пересечения ребер являются вершинами графа. Дуги плоского графа не пересекаются. Стрелки на сетевом графике не должны пересекаться.

Нумерация событий на сетевом графике производится после построения сети. Предпочтительной считается такая нумерация, при которой номер предшествующего события для каждой работы меньше номера последующего события. Исходному событию присваивается номер 1. Затем вычеркиваются все выходящие из него работы после чего несколько событий окажутся без входящих работ. Этим событиям присваиваются номера 2,3,4…N₁ (события первого ранга). Событиям, оставшимся без входящих работ, присваиваются номера N₁+1, N₁+2… N₁+N₂ (события второго ранга) и т.д. до завершающего события. (События могут быть и четвертого, и пятого ранга и т.д.).

Сетевая модель сама по себе не может служить средством управления комплексом работ. Для этого необходимо располагать параметрами сети, т.е. количественными характеристиками сетевого графика. Рассмотрим временные параметры сетевых графиков, включающих параметры событий и работ.

В сетевом графике могут быть полные пути, несовпадающие с критическими, либо частично совпадающие с ними и называются напряженными. Напряженные пути обладают важным свойством: на участках, не совпадающих с критической последовательностью работ, они имеют резерв времени:

R_i.c. = L_k – L_i.c., (21)

где R_i.c. – резерв времени;

L_k – продолжительность критического пути;

L_i.c. – продолжительность ненапряженного пути.

Резерв времени показывает, на какой срок может быть увеличена продолжительность данного пути без изменения срока свершения завершающего события.

К временным параметрам событий относятся:

а) наиболее ранний срок свершения событий;

б) наиболее поздний срок свершения событий;

в) резерв времени свершения события.

Событие считается свершимся, если закончилось выполнение всех работ, входящих в это событие. Следовательно, минимальное время для свершения события определяется по пути максимальной продолжительности, предшествующему этому событию:

ТР = max L_i,j,

L_i,j – продолжительность пути от исходного события i до рассматриваемого события j;

ТР – наиболее ранний срок свершения события j.

В сетевом графике могут быть несколько путей, предшествующих данному событию. Из них выбирается тот, который имеет максимальную продолжительность. Время этого пути и будет равна наиболее раннему свершению события. Наиболее ранний срок свершения события С (обозначает Т_ip) равен L_кр. Для любого события j, которая является последующим за событием i наиболее ранний срок его свершения рассчитывается по формуле

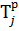= max ( 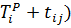, (23)

Где 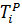– наиболее ранний срок свершения события i, предшествующего событию j;

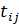– время выполнения работы (i,j).

Задержка свершения события i по отношению к своему раннему сроку не отразится на сроке свершения завершающего события i а значит, и на сроке выполнения комплекса работ до тех пор пока сумма срока свершения этого события и продолжительности (длины) максимального из последующих за ним путей

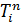=L_k – max_i L_i,c, (24)

где L_i,c – продолжительность пути, последующего за данным событием i.

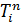= min_j ( 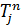-t_ij), (25)

где 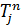– наиболее поздний срок свершения события j, последующего за событием i.

После расчета наиболее ранних сроков свершения события ( 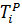) и поздних сроков свершения этого события ( 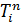)находится резерв времени события j:

R_j = 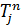- 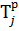(26)

В результате проведения расчета часть событий сети, включая события I и С, будет иметь резерв времени, равный 0. Эти события – критические, и все полные пути, проходящие через эти события и имеющие максимальную продолжительность L_кр, будут критическими. Критические работы на сетевом графике выделяются утолщенными линиями или двойными стрелками.

К временным параметрам работ относятся:

- ранний срок начала работы;

- ранний срок окончания работы;

- поздний срок начала работы;

- поздний срок окончания работы.

Очевидно, что ранний срок начала работы (i,j) обозначаемый как 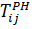, совпадает с наиболее ранним сроком свершения события i, т.е. 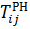= 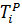(27)

где 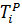– ранний срок наступления начального (предшествующего) события i;

Поздний срок начала работы характеризуется зависимостью

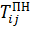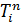= -t_ij, (28)

А срок позднего окончания работы –

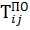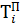= (29)

В каждом сетевом графике существуют работы, у которых сроки позднего и раннего начала или окончания равны. Эти работы лежат на критическом пути и имеют нулевой резерв времени. Работы, не лежащие на критическом пути, имеют резервы времени, отличные от нуля.

В практических расчетах используется, как правило, только полный резерв времени работ. Он характеризует максимальную величину, на которую может быть увеличено время выполнения данной работы без изменения срока завершения комплекса работ в целом. Полный резерв работ (R_ij) рассчитывается по одной из формул:

1) на основе временных параметров событий

R_ij = 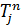- - 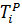t_ij; (30)

2) на основе временных параметров работ

R_ij = 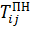- 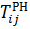, или R_ij = 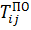- 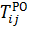(31)

Основой для оптимизации сети служит критический путь и резервы времени.

Под оптимизацией сетевого графика понимается последовательное преобразование сети, приводящее к улучшению организации комплекса работ, более рациональному использованию ресурсов с учетом срока выполнения. Эти преобразования осуществляются за счет:

1) распределения резервов времени между критическими работами и работами с минимальными резервами времени, что фактически означает переброску в разумных пределах материальных и трудовых ресурсов на указанные работы, причем технологически однородные и выполняемые в один и тот же период времени;

2) ускорения выполнения раб критического пути с помощью привлечения дополнительных трудовых ресурсов;

3) параллельного выполнения работ критического пути, если позволяет технология;

4) изменения технологии выполнения комплекса работ;

5) сокращения трудоемкости критических работ за счет передачи части работ на другие пути, имеющие резервы времени.

В процессе сокращения продолжительности работ критический путь может измениться, и в дальнейшем процесс оптимизации будет направлен на сокращение продолжительности работ нового критического пути, и так будет продолжаться до получения удовлетворительного результата (например, выполнения комплекса работ в заданный срок). В идеале длина любого из полных путей может стать равной сумме длине критического пути.

Тогда все работы будут вестись с равным напряжением. А срок завершения проекта существенно сократится.

Математический аппарат оптимизации по нескольким критериям одновременно (например, время, стоимость, ресурсы) отсутствует. Здесь могут использоваться неформальные методы оптимизации – эвристические, основанный на прошлом опыте, интуиции работника, его логике (в т.ч. при оптимизации сетевого графика методом «время-стоимость»). Когда оптимизация проводится по одному критерию (например, время), то могут использоваться методы математического программирования.

После оптимизации сетевого графика по времени осуществляется привязка его к календарю. В результате создается план-график проведения работ, в котором указываются даты наступления событий, начала и окончания работ, величины резервов времени.

Существуют системы СПУ, где время выполнения каждой работы точно неизвестно. Тогда продолжительности работ t_ij рассматриваются как случайные величины, а сети – как вероятностные ( в отличии от ранее рассмотренных детерминированных).

Обработка реальных сетевых графиков (содержащих до десятков тысяч событий) производится по специально разработанным пакетам прикладных программ для ПК. Они позволяют проводить правильные построения сетевого графика, объединить частные графики в единую сеть, нумеровать события, рассчитывать параметры сети, вычеркивать графики на графопостроители, привязывать сеть к календарю.