Примеры решения задач. 4.2.1 Определить показания приборов электромагнитной системы в цепи, схема которой показана на рис

4.2.1 Определить показания приборов электромагнитной системы в цепи, схема которой показана на рис. 4.8, записать выражение мгновенного значения тока и построить временные зависимости напряжения u(t) и тока i(t), если:

ωL=11 Ом, R= 10 Ом.

На вход цепи подано несинусоидальное напряжение, представленное в виде ряда Фурье: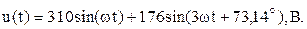

Расчет гармонических составляющих тока и напряжения проведем методом комплексных амплитуд.

Ток основной гармоники:

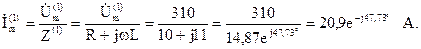
Действующее значение тока первой гармоники:

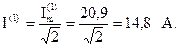
Ток третьей гармоники:

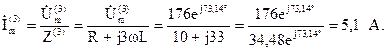
Действующее значение тока третьей гармоники:

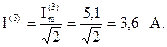
Определим показания амперметра:

.

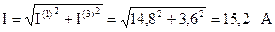Показания вольтметра

,

где действующие значения напряжений гармоник:

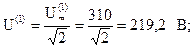
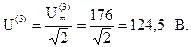
Запишем выражение для мгновенного значения тока:

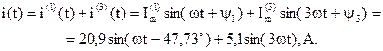
На рис. 4.9 и 4.10 представлены графики временных зависимостей входного напряжения и тока, а также составляющих их гармоник. При вычерчивании кривых отдельных гармоник учитываем тот факт, что период гармоники обратно пропорционален ее номеру. Так как по оси абсцисс откладываем величину ωt, то при построении графика третьей гармоники напряжения ее начальная фаза (73,14°) разделена на номер гармоники ( ).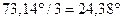

4.2.2 Определить показания амперметра в цепи, схема которой представлена на рис. 4.11, рассчитать активную мощность всей цепи, записать выражение мгновенного значения тока цепи и построить графики временных зависимостей входного тока i(t) и напряжения u(t), если:

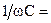11 Ом; R = 10 Ом;

а подведенное напряжение: u(t) = 310sin(ωt) + 176sin(3ωt).

Ток основной гармоники:

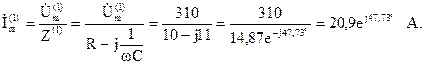
Действующее значение тока первой гармоники:

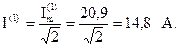
Ток третьей гармоники:

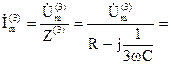
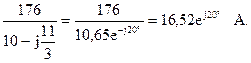
Действующее значение тока третьей гармоники:

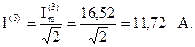
Показания амперметра:

.

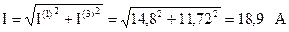Выражение для мгновенного значения тока:

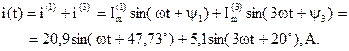
На рис. 4.12 и 4.13 представлены графики временных зависимостей входного напряжения и тока, а также составляющих их гармоник.

Активная мощность цепи:

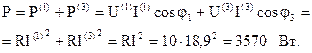
4.2.3Определить показания приборов электромагнитной системы в цепи, схема которой показана на рис. 4.14, записать выражение мгновенного значения тока и построить временные зависимости напряжения u(t) и тока i(t), если:

R = 50 Ом, ωL = 10 Ом, 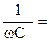90 Ом.

На вход цепи подано несинусоидальное напряжение, заданное в виде ряда Фурье:

u(t) = 100 + 310sin(ωt + 30°) + 106sin(3ωt – 30°).

Рассчитаем токи и напряжения нулевой гармоники.

Постоянная составляющая тока I⁽⁰⁾ в цепи отсутствует, так как сопротивление конденсатора на постоянном токе равно бесконечности Х_С = ∞, то есть конденсатор представляет собой разомкнутый участок цепи. Напряжение постоянной составляющей U⁽⁰⁾ приложено к месту разрыва цепи, то есть к конденсатору:

.

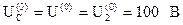Постоянные составляющие напряжений на остальных участках цепи равны нулю.

Рассчитаем токи и напряжения первой гармоники.

Комплексное сопротивление первой гармоники:

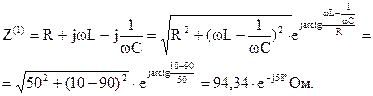
Комплексная амплитуда входного напряжения первой гармоники:

.

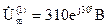Ток основной гармоники:

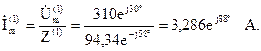
Действующее значение тока первой гармоники:

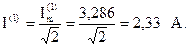
Комплексная амплитуда напряжения первой гармоники на зажимах индуктивной катушки:

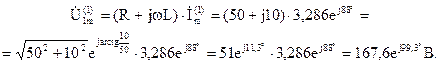
Комплексная амплитуда напряжения первой гармоники на конденсаторе:

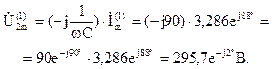
Действующие значения напряжений первой гармоники:

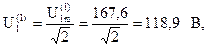
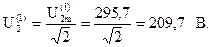
Выполним расчет тока и напряжений третьей гармоники.

Комплексное сопротивление третьей гармоники:

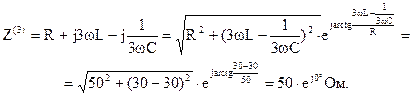
Комплексная амплитуда входного напряжения третьей гармоники:

.

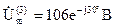Ток третьей гармоники:

Действующее значение тока третьей гармоники:

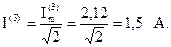
Комплексная амплитуда напряжения третьей гармоники на зажимах индуктивной катушки:

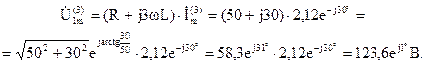
Комплексная амплитуда напряжения третьей гармоники на конденсаторе:

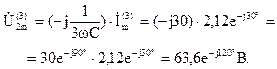
Действующие значения напряжений третьей гармоники:

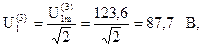
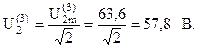
Амперметр измеряет действующее значение входного тока:

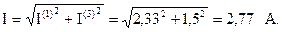
Показания первого и второго вольтметров, также измеряющих действующие значения напряжений:

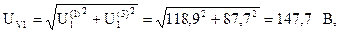
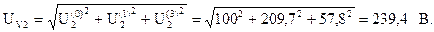
Выражение для мгновенного значения тока можно записать в виде:

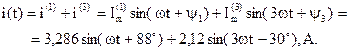
На рис. 4.15 и 4.16 представлены графики временных зависимостей входного напряжения и тока, а также составляющих их гармоник.

При вычерчивании кривых отдельных гармоник учитываем тот факт, что период гармоники обратно пропорционален ее номеру. То есть период третьей гармоники в три раза меньше периода первой гармоники. А так как по оси абсцисс откладываем величину ωt, то при построении графиков третьей гармоники напряжения и тока их начальные фазы необходимо разделить на номер гармоники.

4.2.4 На вход электрической цепи, схема которой приведена на рис. 4.17, подано несинусоидельное напряжение, аналитически заданное в виде разложения в ряд Фурье:

.

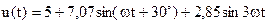Определить показания приботов электромагнитной системы и мощность, потребляемую цепью.

Токи в цепи рассчитываем методом наложения. Расчет для каждой из гармоник будем выполнять в комплексной форме.

Определим постоянную составляющую токов в каждой из ветвей. Так как в цепи постоянного тока конденсатор представляет собой разомкнутый участок цепи, а идеальная катушка короткозамкнутый участок, то нулевая гармоника тока второй ветви отсутствует, а входной ток равен току первой ветви и определяется:

Постоянная составляющая напряжения на зажимах параллельных ветвей равна нулю.

Выполним расчет для первой гармоники.

Сопротивления реактивных элементов для первой гармоники:

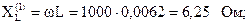
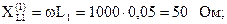
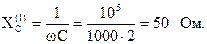
Реактивные опротивления параллельных ветвей равны, то есть в цепи наблюдается резонанс токов и комплексное сопротивление параллельных ветвей:

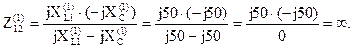
Тогда первая гармоника входного тока равна нулю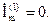

Все входное напряжение первой гармоники приложено к параллельному контуру: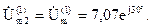

Можно определить комплексные амплитуды токов параллельных ветвей:

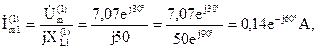
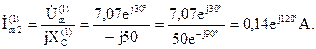
Действующие значения напряжения и токов параллельных ветвей:

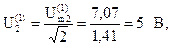
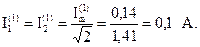
Рассчитаем токи и напряжения для третьей гармоники.

С увеличением намера гармоники индуктивные сопротивления увеличиваются, а емкостные уменьшаются:

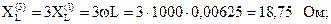
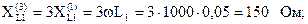
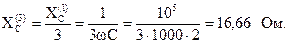
Комплексное сопротивление параллельных ветвей для третьей гармоники:

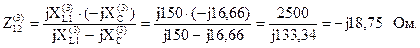
Входное сопротивление для третьей гармоники:

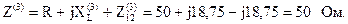
Входной ток: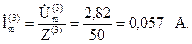

Его действующее значение;

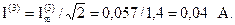
Напряжение на параллельных ветвях:

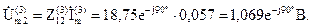
Третья гармоника токов параллельных ветвей:

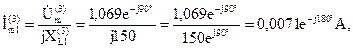
Действующие значения напряжения и токов парал-лельных ветвей:

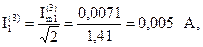
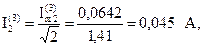
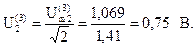
Определим показания приборов. Измерительные приборы электромагнитной системы измеряют действующие значения несинусоидальных токов и напряжений.

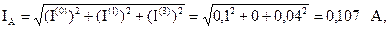
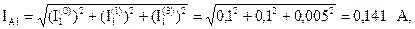
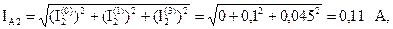
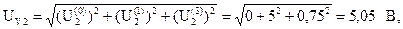
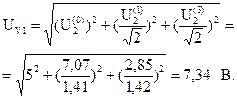
В рассматриваемой цепи активная мощность будет выделяться только в резисторе с сопротивлением R, и она может быть определена:

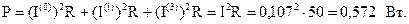
4.2.5На вход электрической цепи, схема которой представлена на рис. 4.18, подано несинусоидальное напряжение:

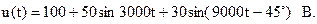
Подобрать емкости конденсаторов С₁ и С₂ так, чтобы в нагрузку не проходила постоянная составляющая и третья гармоника напряжения, а первая гармоника проходила без искажения. Параметры цепи: L = 10 мГн, R_Н = 100 Ом.

Рассчитать мгновенные значения токов и показания приборов электродинамической системы.

Для того, чтобы в нагрузку не проходила постоянная составляющая, необходимо последовательно с нагрузочным сопротивлением включить конденсатор любой емкости, который, как известно, не пропускает постоянный ток. Поэтому постоянные составляющие тока нагрузки 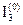и напряжения на его зажимах 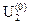будут отсутствовоть.

Для того, чтобы в нагрузке отсутствовала третья гармоника напряжения, необходимо, чтобы в нее не проходила третья гармоника тока, а для этого нужно параллельный контур настроить в резонанс токов на частоте 3ω = 9000 рад/с.

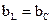или 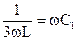, откуда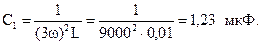

Сопротивление резонансного контура для третьей гармоники будет равно бесконечности и все напряжение этой гармоники будет приложено к параллельному контуру.

Рассчитаем токи третьей гармоники в параллельных ветвях, учитывая, что ток индуктивности отстает от напряжения на 90^°, а ток конденсатора опережает напряжение на такой же угол:

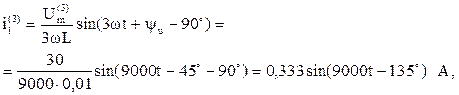
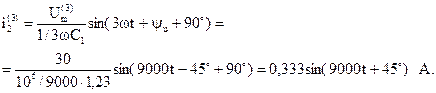
Рассчитаем токи первой гармоники. Расчет будем выполнять в комплексной форме.

Сопротивление параллельного контура первой гармоники:

Для того, чтобы первая гармоника входного напряжения передавалась без искажения, необходимо цепь настроить в резонанс напряжений, то есть чтобы 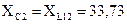Ом, тогда:

Входное сопротивление первой гармоники:

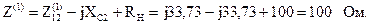
Ток нагрузки: .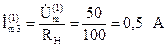

Токи параллельных ветвей:

.

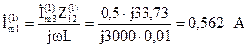
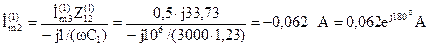Запишем мгновенные значения токов первой гармоники;

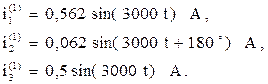
Мгновенные значения несинусоидальных токов ветвей:

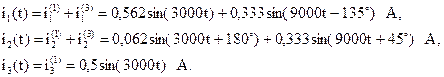Показания измерительных приборов, измеряющих действующие значения токов и напряжений:

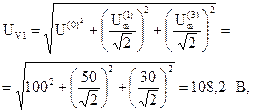
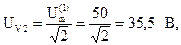
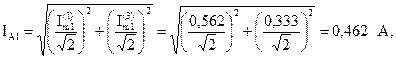
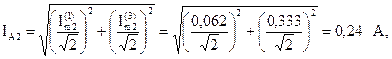
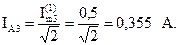
Четырехполюсники

Основы теории

Системы автоматического регулирования энергетических систем, ЭВМ, другие сложные электрические устройства имеют в своем составе блоки, которые связаны с внешней цепью четырьмя зажимами - двумя входными и двумя выходными.

При анализе работы системы в целом такие блоки, зачастую имеющие достаточно сложную внутреннюю структуру, могут рассматриваться как четырехполюсники, служащие для передачи или преобразования энергии или электрических сигналов. Если четырехполюсник не содержит в своем составе источники энергии или содержит источники энергии, но действие их не обнаруживается на входных и выходных зажимах, то такие четырехполюсники называют пассивными. Например, трансформаторы, электрические фильтры, линии электропередач, линии связи и т.д.