Несинусоидальными токами и напряжениями
Если в линейной электрической цепи действует несинусоидальный периодический источник ЭДС (рис. 4.4), то расчет токов и напряжений в такой цепи выполняется следующим образом.
Заданную несинусоидальную ЭДС представляют в виде разложения в ряд Фурье: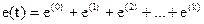 
и на эквивалентной схеме замещения (рис. 4.5, а) представляют в виде последовательного соединения нескольких синусоидальных источников ЭДС различной частоты.
Расчет линейной цепи с несинусоидальными ЭДС и токами выполняется методом наложения и сводится к определению токов и напряжений в нескольких частичных схемах (рис. 4.5, б, в, г). То есть расчет сводится к решению k задач с синусоидальными ЭДС и токами, где k – число синусоидальных составляющих ряда Фурье, и одной задачи с постоянными ЭДС и токами, при условии наличия нулевой гармоники в аналитическом разложении несинусоидальных величин в ряд Фурье. В пределах одной гармоники расчеты можно выполнять в комплексной форме, так как все напряжения и токи в частичной схеме изменяются во времени по синусоидальному закону.
При расчете гармонических составляющих необходимо иметь в виду, что сопротивления индуктивных и емкостных элементов зависят от частоты, то есть от порядкового номера гармоники: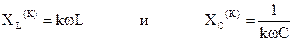 
.
Активное сопротивление при достаточно низких частотах и малых сечениях проводов можно считать независящим от номера гармоники.
  |
В частичной схеме (рис. 4.5, б), являющейся схемой замещения по постоянной составляющей (ω = 0) сопротивление индуктивного элемента ωL равно нулю, поэтому постоянная составляющая напряжения uL(0) также равна нулю. Сопротивление емкостного элемента 1/(ωС) равно бесконечности, то есть он представляет собой разомкнутый участок цепи. Поэтому постоянная составляющая тока ветви, содержащей конденсатор, iC(0) отсутствует.
В цепи (рис. 4.5, в) действует ЭДС первой гармоники е(1)(t)=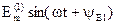 
. Запишем комплексную амплитуду этой ЭДС: 
.
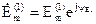Комплексное сопротивление цепи:
.
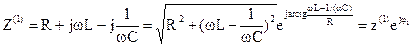Комплексная амплитуда тока:
.
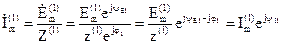Тогда мгновенное значение тока первой гармоники:
.
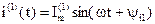ЭДС второй гармоники (рис. 1.5, г):
е(2)(t)=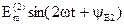 
.
Комплексная амплитуда ЭДС второй гармоники:
.
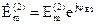Комплексное сопротивление цепи второй гармоники:
.
Комплексная амплитуда тока второй гармоники:
.
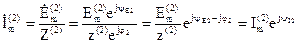Тогда мгновенное значение тока второй гармоники:
.
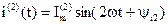Аналогичные расчеты выполняются и для остальных гармоник.
Для k-той гармоники (рис. 4.5, д):
е(k)(t)=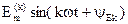 
.
Комплексная амплитуда ЭДС k-той гармоники:
.
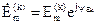Комплексное сопротивление цепи:
.
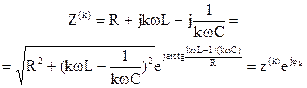Комплексная амплитуда тока:
.
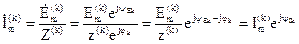Мгновенное значение тока k-той гармоники:
.
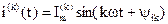Мгновенное значение несинусоидального тока цепи определяется как алгебраическая сумма токов всех гармоник:
i(t) = i(0)(t) + i(1)(t) + i(2)(t) +…+ i(k)(t) = =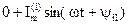 
.
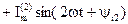
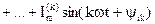Аналогичным образом выполняется расчет несинусоидальных напряжений на отдельных участках электрической цепи.
Для построения графика временной зависимости несинусоидальной функции строят в одних осях координат графики синусоидальных составляющих всех гармоник. При вычерчивании кривых отдельных гармоник необходимо учитывать тот факт, что период гармоники обратно пропорционален ее номеру. А так как по оси абсцисс откладывают величину ωt, то при построении графика k-той гармоники несинусоидальной функции ее начальная фаза делится на номер гармоники.
Таким образом, расчет токов и напряжений в линейных цепях при воздействии несинусоидальной ЭДС выполняется в следующем порядке.
1. Заданные несинусоидальные ЭДС представляют в виде разложения в ряд Фурье.
2. Проводят расчет методом наложения, то есть рассчитывают токи и напряжения в цепи для каждой составляющей ряда в отдельности.
3. Записывают мгновенные значения токов и напряжений, алгебраически суммируя мгновенные значения всех гармонических составляющих.
Дата добавления: 2016-05-25; просмотров: 1443;