Несинусоидальных электрических величин
Первым способом является представление периодических несинусоидальных электрических величин графиками зависимости их мгновенных значений от времени.
На рис. 4.1, а представлен график выходного напряжения диодного ограничителя, на рис. 4.1, б и в изображены графики напряжения на нагрузочном сопротивлении однополупериодного и двухполупериодного выпрямителей.

а)
б)
в)
Вторым способом представления периодических несинусоидальных величин является аналитическое разложение периодических функций в ряд Фурье.
Как известно, любая периодическая функция f(ωt), удовлетворяющая условиям Дирихле, то есть имеющая на всяком конечном интервале конечное число разрывов первого рода и конечное число максимумов и минимумов, может быть разложена в тригонометрический ряд Фурье:
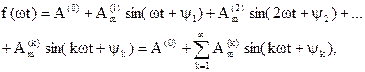
где А(0) называют постоянной составляющей или нулевой гармоникой, второй член разложения 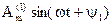 – основной синусоидой или первой гармоникой, период Т которой равен периоду данной несинусоидальной функции, а все остальные члены разложения вида
– основной синусоидой или первой гармоникой, период Т которой равен периоду данной несинусоидальной функции, а все остальные члены разложения вида 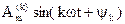 при k > 1 носят название высших гармоник. Гармонические составляющие для краткости часто называют гармониками.
при k > 1 носят название высших гармоник. Гармонические составляющие для краткости часто называют гармониками.
Для несинусоидальных функций токов и напряжений, наиболее часто встречающихся в электротехнике, разложение в ряд Фурье можно найти в справочниках по математике и электротехнике.
В качестве примера приведем разложение в ряд Фурье функций u(ωt), показанных на рис. 4.1, а, б, в:
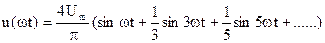 (рис. 4.1, а);
(рис. 4.1, а);
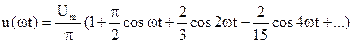 (рис.4.1, б);
(рис.4.1, б);
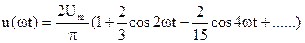 (рис. 4.1, в).
(рис. 4.1, в).
Как видно из приведенных выражений, несинусоидальные напряжения имеют различный состав гармоник в ряде Фурье. В приведенных выражениях начальные фазы гармоник равны нулю. Однако довольно часто начальные фазы имеют ненулевые значения.
Амплитуды и начальные фазы гармоник определяют спектральный состав несинусоидальной кривой. Спектры амплитуд и начальных фаз представлены на рис. 4.2.
На диаграмме амплитудно-частотного спектра (рис. 4.2, а) отложены относительные значения постоянной составляющей и амплитуд остальных гармоник ряда. Значения амплитуд берутся положительными, а их отрицательный знак учи-тывается фазой.

Как правило, амплитуда гармонических составляющих резко уменьшается с ростом номера гармоники, поэтому при анализе электрических цепей несинусоидального тока ограничиваются учетом только нескольких первых членов ряда.
Рис. 4.2
Дата добавления: 2016-05-25; просмотров: 1341;
