Примеры решения задач. 3.2.1Определить линейные и фазные токи и напряжения в трехфазной нагрузке, соединенной по схеме звезда при наличии и отсутствии нулевого провода (рис
3.2.1Определить линейные и фазные токи и напряжения в трехфазной нагрузке, соединенной по схеме звезда при наличии и отсутствии нулевого провода (рис. 3.10). Питание осуществляется от источника с линейным напряжением UЛ = 220В, сопротивления фаз нагрузки одинаковы и равны Zа = Zb = Zc = ZФ = R = 100 Ом.
Построить векторную диаграмму рассчитанных токов и напряжений.

Рис. 3.10
При симметричной нагрузке расчет токов и напряжений для схемы с нулевым проводом и без нулевого провода выполняется одинаково, так как в трехпроводной схеме напряжение смещения нейтрали равно нулю 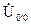 = 0 и, следовательно, фазные напряжения приемников равны фазным напряжениям генератора, а в четырехпроводной схеме ток нулевого провода отсутствует I0 = 0.
= 0 и, следовательно, фазные напряжения приемников равны фазным напряжениям генератора, а в четырехпроводной схеме ток нулевого провода отсутствует I0 = 0.
Фазные напряжения генератора Uфг = UЛ/ 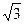 = 220/
= 220/ 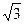 = 127 В.
= 127 В.
Фазные напряжения генератора в комплексной форме записи:
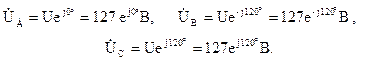
Фазные напряжения приемников равны соответствующим фазным напряжениям генератора:
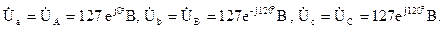
Фазные токи приемников определим по закону Ома:
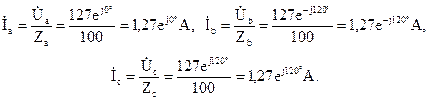
 Построим векторную диаграмму токов и напряжений для режима симметричной нагрузки (рис. 3.11).
Построим векторную диаграмму токов и напряжений для режима симметричной нагрузки (рис. 3.11).
Рис. 3.11
3.2.2Определить линейные и фазные токи и напряжения в трехфазной нагрузке, соединенной по схеме треугольник (рис. 3.12), питающейся от источника с линейным напряжением UЛ = 220В, сопротивления фаз нагрузки одинаковы и равны Zаb= Zbc = Zca = ZФ = R = 100 Ом.
Построить векторную диаграмму рассчитанных токов и напряжений.
 |
Рис. 3.12
Фазные напряжения приемников, при соединении фаз нагрузки треугольником, равны линейным напряжениям генератора, поэтому фазные токи легко определяются по закону Ома:
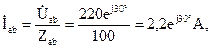
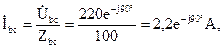
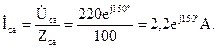
Как видно по расчетам, все токи получились одинаковые по модулю и сдвинуты друг относительно друга по фазе на 120°.
Линейные токи определяем по уравнениям, составленным с помощью первого закона Кирхгофа:
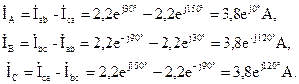
 |
Линейные токи при симметричной нагрузке также получаются одинаковыми по модулю и сдвинутыми друг относительно друга по фазе на 120°. Это хорошо видно на векторной диаграмме токов и напряжений (рис. 3.13).
Рис. 3.13
Линейные и фазные токи приемника при симметричной нагрузке связаны соотношением: IЛ = 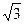 IФ.
IФ.
3.2.3Определить линейные и фазные токи и напряжения в трехфазной нагрузке, соединенной по схеме звезда с нулевым проводом (рис. 3.14). Питание осуществляется от источника с линейным напряжением UЛ = 220В, сопротивления фаз нагрузки: Zа = jXL=j100 Ом, Zb = –jXc= –j100 Ом, Zc = R = 100 Ом. Построить векторную диаграмму токов и напряжений.
В схеме с нулевым проводом фазные напряжения приемника равны соответствующим фазным напряжениям генератора:
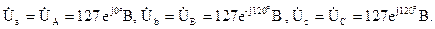
Фазные токи приемников определим по закону Ома:
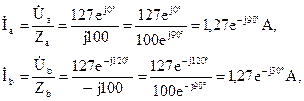
 |
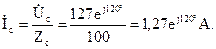
Рис. 3.14
 |
Рис. 3.15
Ток в нулевом проводе определяется с помощью первого закона Кирхгофа:
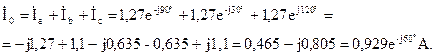
Построим векторную диаграмму токов и напряжений (рис. 3.15).
3.2.4По данным задачи 3.2.3. рассчитать значение активного сопротивления резистора R, включенного в фазу с нагрузки, при котором ток нулевого провода будет равен нулю.
Как видно по векторной диаграмме (рис. 3.15), ток нулевого провода будет отсутствовать в том случае, если действующее значение тока фазы с будет равно сумме токов фаз a и b. Сумма фазных токов:
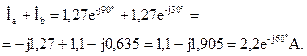
Действующее значение тока фазы с: 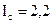 А.
А.
Сопротивление резистора определим по закону Ома:
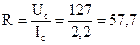 Ом.
Ом.
Дата добавления: 2016-05-25; просмотров: 8723;
