Система географических координат

Для определения положения точки на поверхности Земного сфероида применяют географическую систему координат. В этой системе используют следующие понятия:

Земная ось, это воображаемая линия, вокруг которой происходит вращение Земли. Земная ось пронизывает сфероид в двух точках, называемых географическими полюсами.

Северный полюс, это точка, откуда вращение Земли усматривается против часовой стрелки и обозначается Р_N.

Южный полюс, это антипод северного полюса и обозначается Р_S. Такие географические полюса называют еще истинными.

При пересечении сфероида плоскостями перпендикулярными оси вращения, на его поверхности образуются малые круги называемые параллелями. Если такая плоскость проходит через цент Земли, то ее след на поверхности сфероида образует большой круг называемый экватором.

Следы от пересечения земного сфероида плоскостями, проходящими через ось вращения Земли, называют географическим меридианами или истинными меридианами. В соответствии с решением Международной меридианной конференции (Вашингтон 1884г.) в качестве нулевого (начального) установили меридиан, проходящий через Гринвическую обсерваторию (ее пассажный прибор) вблизи Лондона. Он получил название нулевого или гринвического меридиана. Меридиан, проходящий через точку наблюдения, называется истинным меридианом наблюдателя.

Географической широтой (j) некоторой точки на поверхности земного сфероида называется угол между плоскостью экватора и нормалью к этой поверхности. Широта измеряется дугой меридиана от экватора до параллели точки. Плоскость экватора делит Землю на два полушария – северное и южное. Счет географических широт ведется от экватора к северу (N) или югу (S) от 0° до 90°. В алгеброических расчетах они имеют знаки (+) северная и (-) южная широта.

геоида применяется сфера, то в этом случае нормаль к поверхности совпадает с направлением на центр

Расчетная формула будет: РШ (Dj) = j₂ - j₁.

Разность долгот (Dl) это наименьшая из дуг экватора, заключенная между меридианами точки отхода (l₁) и точки прихода (l₂). Пределы изменения разности долгот от 0° 180° и, если плавание осуществлялось в сторону востока (Е), то она имеет знак (+), если же в сторону запада (W), то у нее знак (-).

Расчетная формула будет: РД (Dl) = l₂ - l₁.

Формулы расчетов РШ и РД определяют не только их величины, но и наименование или знак (+ ; -).

l₂ l₁

j₂ В

j₁

А

Рис. 42

На рисунке (Рис. 42) разность широт сделана к норду (N) и разность долгот к западу (W). Стрелка наглядно показывает, как плавало судна из точки отхода (А) в точку прихода (В).

3. Морские единицы длины и скорости.

В процессе судовождения решаются задачи с измерением углов и угловых расстояний. Для измерения расстояний метрическая система для мореплавателей неудобна. В качестве основной единицы длины в практике мореплавания принята длина одной минуты дуги меридиана земного эллипсоида. В метрической системе длина одной минуты дуги меридиана выражается формулой:

D = 1852,23 – 9,34 Cos 2j.

Как видим, длина одной минуты дуги меридиана величина непостоянная и зависит от широты места, что неудобно для использования на практике. В 1928 году Международное гидрографическое бюро в качестве международной, стандартной морской мили приняло постоянную величину равную 1852 метрам.

Одна десятая часть морской мили называется кабельтов (кб) 1 кб = 0,1 мили = 185,2 метра.

За единицу скорости в морской навигации принят узел. 1 уз. = 1 миля/час.

Понятие «узел» пришло в морскую навигацию из эпохи парусного флота, когда скорость измерялась по длине вытравленного за борт судна лаглиня, прикрепленного к деревянному сектору. Лаглинь разделялся узелками на части, равными 1/120 мили. Скорость измерялась в течении 30 секунд по песочным часам, что составляло 1/120 часа. Таким образом, количество вытравленных за борт «узлов» на ходу судна за 30 секунд соответствовало количеству миль, пройденных за час.

Переход от скорости в узлах к скорости в кабельтовых в минуту производится по формуле: V_{кб/мин = .}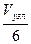

При использовании некоторых картографических материалов других стран могут встречаться и другие единицы длины:

Морская сажень = 1,828 м или = 6 фут (применяется при обозначении глубин).

Фут = 30,48 см = 12 дюймов (применяется для обозначения высот побережья, малых глубин и осадки судна).

Ярд = 91,44 см = 3 футам (используется для измерения небольших расстояний в США и Англии).

Дюйм = 2,54 см (применяется как доля фута и при измерении различных диаметров).

11.4. Деление горизонта и системы счета направлений

Счет направлений в море относительно истинного меридиана является основополагающим. Предположим что наблюдатель находится в некоторой точке А на поверхности Земли. Проведем мысленно плоскость (Н) перпендикулярную отвесной линии в данной точке. Это плоскость называется плоскостью истинного горизонта. Представим, что через точку А проходит другая, уже упоминавшаяся плоскость истинного меридиана (М). Эта плоскость называется плоскостью истинного меридиана наблюдателя (точка А) и в пересечении с плоскостью истинного горизонта образует линию истинного меридиана наблюдателя. Плоскость, проходящая через точку А перпендикулярно плоскости истинного меридиана называется плоскостью первого вертикала (V), в пересечении с плоскостью истинного горизонта образует линию перпендикулярную линии истинного меридиана. Линия истинного меридиана является полуденной линией и определяет направление на северный и южный полюса (N – S). Линия, перпендикулярная линии истинного меридиана, дает направление E – W. Эти линии (N-S и E-W) в любой точке земной поверхности (кроме полюсов) занимают строго определенное положение и служат для ориентирования.

V

M W

S N

H E P_N

Рис. 43

Направления N, S, E, W называются главными направлениями или главными румбами и делят плоскость истинного горизонта на четыре четверти (NO, SO, SW, NW). Направление, делящее каждую четверть пополам, называются четвертными румбами и имеют обозначение, соответствующее названию четверти (NO, SO, SW, NS).

В зависимости от конкретных задач судовождения применяются следующие системы счета направлений:

В круговой системе счета плоскость истинного горизонта делится на 360 градусов, причем за начало принято

В полукруговой системе счет направлений ведут от главных румбов N

или S в сторону востока Е или запада W от 0° до 180° (N 120 O; S 120 O; S 60 O; S 60 W).

В четвертной системе счет направлений ведут от главных румбов N или S в каждой четверти от 0° до 90°, присваивая обозначение наименований четверти (NO 30; SO 30; SW 50; NW 50).

В румбовой системе счет направлений ведут от направления на север (N) по часовой стрелке в румбовых величинах, а не в градусах. В этой системе истинный горизонт делится на 32 части (румба). Угол между двумя смежными направлениями получил название румба, величина которого в градусной мере составляет:

.

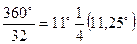Все 32 румба имеют собственные наименования и применяются в основном при определении направлений течения и ветра. Слово «румб» используется также как термин, обозначающий направление на любую точку в море.

Положение судна принято фиксировать углом между диаметральной плоскостью (ДП) судна и плоскостью истинного меридиана. Диаметральная плоскость это условная вертикальная продольная плоскость, делящая корпус судна на две симметричные части (левый и правый борт). Она пересекается с плоскостью истинного горизонта (Н) по прямой линии – линии истинного курса.

Истинный курс (ИК) это двугранный угол между нордовой частью плоскости истинного меридиана и носовой частью диаметральной плоскости судна. Если направления брать для плоскости истинного горизонта (Н), то определение истинного курса будет проще – как плоский угол между нордовой частью истинного меридиана и носовой частью диаметральной плоскости судна (линией курса).

Истинный пеленг (ИП), это двугранный угол между нордовой частью плоскости истинного меридиана и плоскостью вертикала, проходящей через ориентир. Или плоский угол между нордовой частью истинного меридиана и направлением на ориентир.

Направление, отличающееся от направления истинного пеленга на 180°, называется обратным истинным пеленгом (ОИП). ОИП = ИП ± 180°.

Угол между линией курса и линией пеленга называется курсовым углом (КУ).

В круговом счете истинный курс и истинный пеленг отсчитываются от 0° на северной части истинного меридиана, а курсовой угол от носовой части линии курса (по часовой стрелке). В полукруговом счете ИК и ИП, как правило, не считаются, исключая азимут (название применяется к направлениям вместо пеленга). Курсовой угол считается от носовой части линии курса до 180° на правый (пр/б) и левый (л/б) борт. Если курсовой угол ориентира равен ± 90°, то говорят, что ориентир находится на траверзе судна. В четвертном счете ИК, ИП, КУ, кроме азимута не считаются. Соотношение между ИК, ИП, и КУ выражается формулой: ИП = ИК ± КУ ((+)пр/б, (-) л/б).

Если курсовой угол получится больше 180°, нужно взять дополнение до 360° и сменить наименование курсового угла (КУ пр/б на КУ л/б и наоборот).

N_И Если при расчете получается,

что истинный пеленг больше

360 градусов,то нужно вычесть из

из результата 360°. В том случае,

если КУ > ИК и он левого борта, то

ИК к ИК прибавляют 360°.

N_И КУ = ИП - ИК

Эта формула расчета курсо

ИП вого угла позволяет опреде -

лить не только величину, но

КУ инаименование курсового

угла (если результат имеет

знак (-), то КУ будет л/б,.а если знак (+), то КУ будет

ОИП пр/б

11.5. Видимый горизонт и дальности видимости предметов

Наблюдаемая с судна линия (окружность), по которой соединяется поверхность Земли с небесным сводом, называется видимым горизонтом наблюдателя. Расстояние от наблюдателя до этой линии называется дальностью видимого горизонта. Эта дальность зависит в основном от высоты глаза наблюдателя над поверхностью моря и определяется выражением: D_е = 2,1 .

Любой предмет, характеризующийся высотой (Н) над уровнем моря, так же как и глаз наблюдателя, будет иметь свою дальность видимого горизонта (D_Н). Дальность видимости предмета (D_П) складывается из дальностей видимости горизонта наблюдателя и предмета, т.е. D_П = D_Н + D_е = 2,1 (ÖН + Öе)

Рис. 46

На морских навигационных картах дальность видимости предмета дается для высоты глаза наблюдателя 5 метров (е = 5 м.) и обозначается Dк. D₅ = 2,1Ö 5 = 4,7 мили

Dк = Dн + D₅ = Dн + 4,7

Для оперативного решения задачи по расчету дальности видимости предметов в Мореходных таблицах (МТ – 75) помещена таблица № 22, в которой по высоте предмета и или глаза наблюдателя находят дальности видимости горизонта.

11.6. Простое графическое счисление пути судна

Счислением называется вычисление текущих координат судна от известных координат по времени, курсу и скорости. Счисление, выполненное непосредственно на морской навигационной карте с использованием штурманского прокладочного инструмента (параллельная линейка, транспортир и циркуль измеритель), называется графическим или прокладкой. Если счисление выполняется по формулам и таблицам, оно называется аналитическим (письменным). Основным методом непрерывного учета положения судна является графическое счисление. Оно заключается в систематическом нанесении положения судна на карту по данным о его движении по курсу и пройденному расстоянию, а также исходя из данных о течении и дрейфе. Начальная точка счисления должна быть известна. Место судна, координаты которого получены по счислению, называются счислимым.

Контроль прокладки производится путем измерения различных навигационных параметров (пеленгов, расстояний, разности расстояний и высот светил) и получения места судна путем обсервации по двум, трем и более линиям положения.

Геометрические величины, измеряемые непосредственно или же получаемые косвенным путем для определения места судна в море по береговым и небесным светилам называются навигационными параметрами.

Геометрическое место точек, отвечающих постоянному значению величины, измеренной для обсервации (навигационного параметра) называется изолинией. Изолиния в общем случае является кривой линией. Для обсервации необходимо иметь лишь небольшие отрезки изолиний в точке пересечения их под углом друг к другу. Отрезки изолиний без особой погрешности можно заменить отрезками прямых, касательных к изолинии или секущих ее. Касательная или секущая к изолинии называется линией положения. Изолиниями могут быть пеленг, изостадия, (окружность), изогона (окружность), гипербола.

Все графические работы, выполняемые на карте, состоят из отдельных элементов задачи. К таким задачам относят снятие с карты координат судна или нанесения места судна на карту по известным координатам, расчет и прокладка курсов и пеленгов, измерение расстояний между определенными точками. При ведении прокладки решаются задачи двух типов: прямая и обратная.

Первая (прямая) задача предусматривает только учет движения судна, когда курс рулевому задан.

ИК = КК + Dк.

Рассчитывают истинный курс и прокладывают на карте линию курса в виде прямой от исходной точки. При отсутствии сноса от течения и ветра (дрейфа) линия истинного курса будет совпадать с путевым углом, следовательно, судно будет перемещаться по проложенному на карте курсу. На карте у точки, принятой за исходную для ведения счисления, надписывается время с точностью до 1 минуты и отсчет лага с точностью до 0,1 мили ( 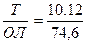). Дальнейшее нанесение положения судна на любой момент времени производится по расстоянию, пройденному судном по лагу от исходной точки. Положение судна на линии проложенного курса отмечается каждый час при плавании вблизи берегов и каждую вахту – при плавании в открытом море, а также при любом изменении курса или скорости. Каждую счислимую точку обозначают чертой длиной около 5 мм, перпендикулярной предшествующему курсу, а каждую обсервованную точку специальным знаком, присвоенным данному виду обсервации.

В практике судовождения обратная задача встречается гораздо чаще и состоит в том, что судну необходимо следовать заданным ИК. В этом случае рулевому задается предварительно рассчитанный КК, исходя из проложенного ИК.

КК = ИК - Dк.

Если необходимо рассчитать отсчет лага на момент прихода в заданную точку поворота, то предварительно снимают с карты расстояние (S), которое необходимо пройти от исходной точки до точки поворота.

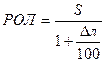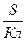= и ОЛ₂ = ОЛ₁ + РОЛ

Время прихода в расчетную точку рассчитывают:

T₂ = T₁ + DT = T₂ +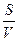

Вдоль линии курса надписывается компасный курс судна и затем в скобках поправка компаса с ее знаком.

30¢

+

+

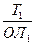
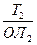
47°

04°00Е 04°20¢

Рис. 47

Прямая задача Обратная задача

КК – задан ИК – снят с карты

+(±)d - из табл. девиации по КК -(±)d – с карты

МК – магнитный курс МК – магнитный курс

+(±)d – склонение с карты-(±)d - из табл. девиации

ИК КК

В прямой задаче выбранные склонение и девиация со своим знаком складываются, а обратной задаче вычитаются.

11.7. Учет дрейфа и постоянного течения при прокладке.

Дрейфом судна называется смещение движущегося судна с линии истинного курса под воздействием ветра. Дрейф судна создается кажущимся ветром. Направлением ветра называют то направление, откуда он дует (говорят: ветер дует в компас). Если ветер дует в левый борт судна, то говорят: судно идет левым галсом, по отношению к ветру. Если дует в правый борт, то судно идет правым галсом. Направление равнодействующей сил давления ветра (Р) в общем случае не совпадает с направлением вектора скорости кажущегося ветра (W). Разложим эту силу (Р) на две составляющие: продольную (Р₁) и поперечную (Р₂).Величина угла дрейфа зависит от многих факторов: осадки, размеров и формы надводной и подводной частей корпуса судна, курсового угла и скорости кажущегося ветра, скорости хода судна. Для учета дрейфа при прокладке необходимо знать угол дрейфа. Имеется ряд способов его определения, но все они не являются точными, что приводит иногда к значительному отклонению от намеченного на карте пути. При учете дрейфа на карте прокладывается только линия путевого угла дрейфа (ПУa).Поперечная составляющая Р₂ вызывает

Р_N дрейф судна, поэтому при

ветре судно перемещается

относительно воды не вдоль

W _a ИК диаметральной плоскости,

ПУ а под некоторым углом к ней (a),

В называемом углом дрейфа.

a Линия АВ, по которой переме-

А щается судно, называется линией

Р₁ пути при дрейфе, а угол ПУ_a,

который она составляет с истин

Р₂ ным меридианом – путевым уг

лом дрейфа

Рис. 48

.

ПУ_a =- ИК + a. ИК = ПУ_a - a.

При ветре левого галса знак при угле дрейфе a (+), а при ветре правого галса знак при угле дрейфа a будет (-).

Так как лаг учитывает влияние ветра на скорость судна (Р₁), то и расстояние можно учитывать, откладывая по линии пути

Sл = РОЛ Кл

Расчеты по прямой и обратной задачам удлиняются по сравнению с расчетами без влияния ветра.

КК ПУ_a с карты

+(±)d из таблицы-(±)a принят для счисления

МК ИК

+(±)d с карты-(±)d с карты

ИК МК

+(±)a принят для счисления-(±)d с карты

ПУ_a КК

Поступательное движение водной массы в морях и океанах называется течением. Элементами течения являются его скорость и направление. Направление течения определяется мнемоническим правилом: «течение идет из компаса». Направление течения показывают в градусах, а иногда в румбах, скорость выражается в узлах.

Под действием упора движителя, судно получает движение относительно воды по направлению диаметральной плоскости (Vл).

Если вода имеет движение относительно Земли, то скорость судна относительно Земли определится геометрической суммой скоростей:

V̅ = V̅л + V̅т

И судно будет перемещаться по направлению вектора V. Если скорость судна Vл и течения Vт постоянны по величине и направлению, то и суммарная скорость V̅ также будет неизменна и судно пойдет по прямой АС.

Угол ПУ между северной частью истинного меридиана и направлением движения судна называется путевым углом (путем), а линия пути АС будет линией пути на течении.

Nи

ПУ В

DТ Vт

ИК Vл Vт b

C

А V

Рис. 49

Угол b между линиями истинного курса (ИК) и путевым углом (ПУ) называется углом сноса от течения. Скорость V будет истинной скоростью судна (относительно дна).

ПУ = ИК + (±)b, ИК = ПУ – (±)b.

Знак у b зависит от направления сноса. Если течение направлено в левый борт, то знак у b (+), а если в правый борт, то знак у

b (-). Учет течения сводится к решению треугольников скоростей. Вначале графически складывают векторы скоростей судна и течения, в итоге получая направление движения судна (ПУ), а затем решают путевой треугольник АВС. Различают прямую и обратную задачи графического решения треугольника скоростей.

Прямая задача.

Nи В прямой задаче по за-

В данным ИК, Vл, Кт и Vт

требуется рассчитать b,

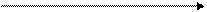
Vт ПУ и V. Для получения

С линии пути ПУ из точки

Vл А проводим линию ИК и

на ней от точки А отк-

ладывают отрезок, рав-

А ный вектору скорости

Рис. 50 судна по лагу (Vл) в

условном масштабе.

Обычно берется количество миль в масштабе карты, проходимое судном на час или полчаса. Из конца вектора скорости судна (Vл) проводим вектор скорости течения (Vт) в том же масштабе. Соединив точку А с концом вектора скорости течения (Vт), получим линию пути судна (ПУ). Снимаем с карты направление этого пути для сравнения с истинным курсом (ИК) и получения угла сноса от течения (b).

b = ПУ – ИК

Для получения счислимой точки за любой промежуток плавания по путевому углу, необходимо по линии истинного курса (ИК) отложить пройденное по лагу расстояние (Sл = РОЛ Кл). Полученную на ИК точку сносим по линии направления течения на линию путевого угла (ПУ) (точки В и С). Надписи на карте производятся над или под линией пути (ПУ) и параллельно ей. Порядок записи таков: пишется ГКК рядом в скобках его поправка, а затем величина сноса от течения со своим знаком (ГКК 69° (-2°) b = +6°).

КК

+(±)d из таблицы девиации

МК

+(±)d с карты

ИК

+(±)b из построения

ПУ_b

Обратная задача

В этой задаче необходимо по заданному ПУ_b, Vл, Кт и Vт рассчитать угол сноса течением (b) и ИК. Задача решается следующим образом -

пусть на карте проложена линия ПУ (АК). Из начальной точки А прокладываем вектор скорости течения Vт, выраженный количеством миль

за полчаса или час. Из конца вектора Vт раствором циркуля, равным

величине скорости суда Vл за тот же промежуток времени, делаем на линии ПУ судна засечку (точка К). Соединив точку К с концом вектора

Nи

D

В

С К

Sл

b

А Vс

Vт

Т

Рис. 51

Sл находим на линии ИК точку В, и затем через точку В проводим линию параллельную вектору скорости течения Vт. Пересечение этой линии с линией ПУ и будет счислимым местом судна (точка С).

ПУ_b направление, снятое с карты

-(±)b получен расчетным путем (ПУ – ИК)

ИК

-(±)d с карты

МК

-(±)d из таблицы девиации по МК

КК

Кроме графического учета течения существует и аналитический, который применяется при автоматизации судовождения.

Совместны учет дрейфа течения

При одновременном действии ветра и течения судно будет подвергаться как дрейфу от ветра, так сносу течением. Угол, на который линия пути отклонится при этом от линии истинного курса (ИК), называется суммарным углом сноса (С).

С= ПУ – ИК С= a + b

Знак угла суммарного сноса (С) получается из приведенной формулы: если ПУ >ИК, то знак будет плюс (+), если ПУ < ИК, то знак будет минус (-). Если же известны величины угла дрейфа (a) и угла сноса течением (b), то знак суммарного сноса определится из алгебраического их сложения.

При наличии ветра и течения решаются также прямая и обратная задачи, как и при наличии только течения. При решении прямой задачи сначала учитывают дрейф и на карту наносят линию пути ПУa. Затем учитывают течение, строя треугольник скоростей, причем скорость судна откладывается по линии путевого угла дрейфа (ПУa), а не по линии ИК.

В обратной задаче при заданном ПУ решают треугольник скоростей, при этом из построения получают не направление ИК, а направление ПУa. Затем снимают направление пути дрейфа (ПУa) и находят истинный курс: ИК = ПУa - a,

а также b = ПУ - ПУa и С= a + b.

На карте под линией путевого угла делается запись о компасном курсе, его поправке и о суммарном угле сноса (ГКК 100 (-2) С= -12)

В общем виде решение задачи выглядит таким образом:

Прямая задача Обратная задача

КК ПУ

+(±)d из таблицы девиации - (±)b из построения

МК ПУa

+(±)d с карты -(±)a принятый

ИК ИК

+(±)a принятый для счисления - (±) d с карты

ПУa МК

+(±)b -(±) d из таблицы дв.

ПУ КК

11.8. Учет циркуляции при графическом счислении

Циркуляция судна это кривая, описываемая центром масс судна при руле, положенном на какой-либо угол. Существует несколько методов учета циркуляции:

М а) точка поворота известна и нужно описать

В окружность, а к ней провести касательную,

параллельную новому курсу (Рис. 52). Это и бу

А дет новая линия курса. Конец поворота будет

в точке А. Чтобы описать окружность

нужно из точки начала поворота (В)

восстановить перпендикуляр к линии старого

курса и по нему от точки В отложить расстояние

Рис. 52 ((а) и б)) равное радиусу циркуляции (Rц). Получим

точку О центр окружности, по которой судно

будет перемещаться при повороте на новый курс.

б) Точка поворота не известна, но на карте проложен новый курс (Рис. 52). Продливаем линию нового курса до пересечения с предыдущим. Получим точку М, место их пересечения. Разделим внутренний угол пополам, проведя биссектрису этого угла. На биссектрисе находим раствором циркуля такую точку О, в которой окружность, проведенная радиусом Rц касается обеих линий проложенных курсов (А и В). Существуют и другие методы учета циркуляции. В них путем расчете определяют точки начала и конца поворота, а также плавание Sл на циркуляции (Рис. 53).

а) б)

М

C

В a

А n

В m

Рис. 53

а) d = 2 Rц Sin d₁ = Rц tg Sл = (метод Домогарова)

б) Sл = Кл РОЛ m 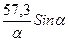= S n = S 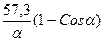(метод Андреева).

Здесь: d – длина промежуточного курса ( 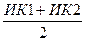или ИК1 ± ),

d₁ – расстояние от точки пересечения курсов до точек начала и конца поворота,

Sл – плавание по лагу на циркуляции,

a - величина угла поворота на новый курс.

Rц – радиус циркуляции,

m – расстояние на продолжении предыдущего курса от точки начала поворота,

n – расстояние на перпендикуляре к предыдущему курсу, проведенному из конца отрезка m до точки конца поворота.

11.9. Курсоуказатели на судне.

Магнитный компас. Одним из типов курсоуказателей на судне является магнитный компас, работа которого основана на использовании магнитного поля Земли. Магнитное поле Земли в любой точке ее поверхности характеризуется вектором напряженности (Т). Одним из элементов этого вектора является горизонтальная составляющая (Н) и магнитное склонение (d). Вертикальная плоскость, содержащая в себе векторы Т и Н, называется плоскостью магнитного меридиана, а след ее пересечения с плоскостью истинного горизонта есть линия магнитного меридиана. Магнитное склонение это угол в плоскости истинного горизонта между истинным и магнитным меридианами. В различных точках Земли магнитный меридиан может быть отклонен к Е или W от истинного меридиана. Магнитное склонение (d) может иметь знак (+) Е или (-) W.

Магнитное поле Земли не постоянно по времени. На основе данных магнитных

съемок составляются карты магнитного склонения с учетом годового его изменения. На морских навигационных картах в различных местах ее поля наносится величина магнитного склонения в градусах и его и его долях. В заголовке карты или у значений магнитного склонения показанного на карте пишется

Nм Nи Nм

его годовое изменение. При ориентации в море по

магнит ному компасу для учета склонения приводят

-d +d его к году плавания. На карте показывается годовое

изменение (увеличение или уменьшение) и относит

ся в абсолютной величине склонения (d). Изменение

магнитного склонения впервые было замечено Ко

лумбом в первом его плавании к берегам Америки в

1492 году. Склонение изменяется в широких преде-

лах от +180° до -180°. Так как направление на гео-

графический полюс не совпадает с направлением

на северный магнитный полюс (76N 100W) и южный магнитный полюс (68S 144Е), то вводится понятие магнитных направлений.

Магнитный курс (МК) и магнитный пеленг (МП) определяются также как и ИК и ИП, но относительно не истинного, а магнитного меридиана. Алгебраические связи ИК и МК выглядят так:

ИК = МК + d ИП = МП + d.

К сожалению, магнитный компас на судне находится под воздействием

Nи не только магнитного поля Земли. Его стрелки

Nм устанавливаются в направлении суммарного вектора напряженности магнитных полей Земли и судна.

МК Компас показывает так называемое компасное

ИК направление, т.е. на условный компасный полюс

d или «норд компасный».Это направление определяет

компасный меридиан, а угол между северными частями магнитного и компасного меридианов

Рис. 55называется девиацией магнитного компаса (d). Если

компасный меридиан отклонен к Е от магнитного меридиана, то девиация восточная будет иметь знак плюс (+), а если к W, то девиация западная имеет знак минус (-),( Рис. 56 а.).

Необходимо отметить, что компасные направления: компасный курс и компасный пеленг определяются по аналогии с ИК и ИП но относительно компасного меридиана.

Nм Nи

а) Nк Nм Nк б) Nк МК

МП

-d +d ИК

ИП

КП КУ

КК

Рис. 56

Формулы для связи компасных, магнитных и истинных направлений очень просты:

МК = КК + d МП = КП + d

ИК = КК + d + d ИП = КП + d + d

Существует понятие обратного магнитного и обратного компасного пеленга (ОМП и ОКП).

ОМП = МП ± 180° ОКП = КП ± 180°.

Алгебраическая сумма склонения (d) и девиации (d) называется поправкой магнитного компаса: Dмк = d + d.

ИК = КК + Dмк ИП = КП + Dмк.

На первых этапах изучения навигации необходимо уметь осуществлять проверку решений по выше приведенным формулам с помощью рисунков или «жучков».

Гирокомпас. В настоящее время на судах в качестве основного курсоуказателя применяется гироскопический компас, работа которого не зависит от магнитного поля Земли.

При установке на судне гирокомпаса добиваются, чтобы курсовая черта этого прибора была сориентирована с ДП судна (в ДП или ей параллельно). По ряду причин не удается точно установить гирокомпас в ДП судна, а значит сориентировать его относительно истинного меридиана. Направление, которое он фиксирует, называется условным гироскопическим меридианом (нордом гирокомпасным). Для получения направления на истинный север необходимо вводить поправку, называемую «поправка гирокомпаса (Dгкк).

Поправкой гирокомпаса (Dгкк) называется угол между нордовыми частями истинного и гирокомпасного меридианов.

Nгк Nи Если Nгкк размещен к востоку (Е) от

ИК истинного, то поправка будет иметь знак

плюс (+). Если же ГКК меридиана расспо-

Dгк ложен к западу (W) от истинного мери-

ГКК ГКП диана. То знак будет (-).

ИК = ГКК + (±)D_гкк

ИП ИП = ГКП + (±)D_гкк

Прямая и обратная задачи по показаниям

гирокомпаса решаются так:

Рис. 57

ГКК ИК

+(±) Dгкк -(±) Dгкк

ИК ГКК

11.10. Пройденное судном расстояние

Приборы, показывающие пройденное расстояние и скорость (лаги), имеют погрешность в показаниях. Эта погрешность компенсируется поправкой лага (Dл). Такая поправка выражается в процентах к пройденному расстоянию и определяется на мерной линии, после регулировки прибора.

Dл = 100 %.

Если поправка лага известна, пройденное расстояние рассчитывают через коэффициент лага (Кл). Кл = 1 + .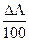

Мерная линия – это специальный полигон, оборудованный секущими створами. Развив необходимую скорость, судно ложится на истинный курс пробега, который, как правило, перпендикулярен секущим створам. Небольшое рыскание в пределах трех градусов не окажет заметного влияния на точность результатов, так как Cos 3° = 0,999. Имея отсчет лага (ОЛ₁) и время (t₁) (с точностью до секунды) на первом створе и (ОЛ₂) и t₂ на втором створе, рассчитывают поправку лага и скорость судна на заданном режиме работы главной силовой установки.

₁t, ОЛ₁ t₂, ОЛ₂

S

t₄, ОЛ₄ t₃, ОЛ₃

Рис. 58

Рассчитываем скорость судна относительно грунта:

Первый пробег: V₁ = ,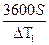

Второй пробег V₂ = тогда скорость судна относительно воды будет: Vл = .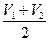

Рассчитываем пройденное расстояние по лагу (Sл) за оба пробега:

Sл = и разность отсчетов лага за это же время:

SРОЛ = (ОЛ₂ – ОЛ₁) + (ОЛ₄ – ОЛ₃), отсюда Кл = 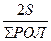, а затем и поправка лага (Dл): Dл = (Кл –1)100.

Здесь: S – расстояние между створами на мерной линии,

t₁ – отсчет времени по судовым часам в момент прохода первого створа мерной линии,

t₂ – отсчет времени по судовым часам в момент прохода второго створа на мерной линии в туже сторону.

t₃ – отсчет времени по судовым часам при проходе начального створа на мерной линии при движении в обратном направлении,

t₄ – отсчет времени по судовым часам при проходе второго створа на мерной линии при движении в обратном направлении,

Sл – пройденное судном расстояние исходя из скорости по лагу.

DТ – время в секундах, затраченное на пробег судна между створами на мерной линии в ту или другую сторону,

Vл - скорость судна, показываемая лагом,

V₁ и V₂ – скорости судна относительно грунта на прямом и обратном пробегах.

11.11. Аналитическое счисление.

Кроме графического счисления, учет движения судна можно производить по формулам – аналитическим методом. Аналитическим счислением называется вычисление приращений (РШ(Dj) и РД(Dl) к исходным координатам(j,l). Аналитическое счисление может быть табличным и автоматизированным, когда для решения приращений (Dj) и (Dl) применяется ЭВМ.

При известных координатах точки отшествия (j₁ и l₁) и их приращений (Dj) и (Dl) легко получают координаты точки прибытия (пришествия j₂ и l₂). j₂ = j₁ + Dj и l₂ = l₁ + Dl.

Значения Dj (РШ) и Dl (РД) можно рассчитать по элементам движения судна курсу (К) и пройденному расстоянию (S).

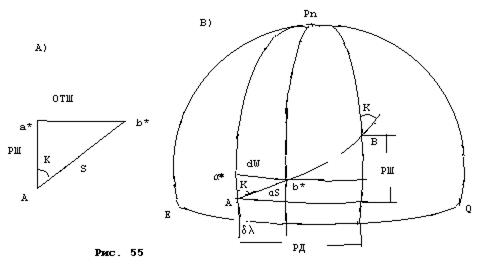
Считая Землю за сферу, рассмотрим треугольник А а* b*(позиция А).

Этот треугольник мал, и его можно считать плоским. Тогда сторона А а* будет равна элементарно малому отрезку меридиана, называемому разностью широт (РШ). Сторона а* b* соответственно элементарно малому отрезку параллели, называемому отшествием (ОТШ). Сторона А b* соответственно элементарно малому отрезку локсодромии (S). Из треугольника находим:

РШ = S Cos K ОТШ = S Sin K.

Из условия построение морской навигационной карты известно, что

РД = РМЧ tg K или РД = .

По приведенным формулам в Мореходных Таблицах (МТ-75) составлены: таблица №24 –где по известным курсу К) и плаванию (S) находят разность широт (РШ) и отшествие (ОТШ), и таблица 25 – где по отшествию (ОТШ) и средней широте (j_m) находят разность долгот (РД).

Определив РШ и РД, рассчитывают координаты точки пришествия.

Аналитическое счисление может быть простым, составным и сложным.

Простое аналитическое счисление выполняется, когда судно следует одним курсом.

Составное аналитическое счисление производится при следовании судна несколькими курсами, координаты конечной точки рассчитываются по сумме РШ и ОТШ всех курсов.

Сложное аналитическое счисление тоже производится при следовании судна несколькими курсами, но вычисляют РШ и РД для каждого курса в отдельности.

11.12. Определение места судна.

Как бы тщательно не велось счисление пути судна, оно не может обеспечить безопасность плавания. Возможные погрешности в поправках навигационных приборов (компаса, лага), не точное знание элементов течения, трудности в определении величины угла дрейфа – все это приводит к значительным погрешностям в счислении и, как итог, отклонение судна от заданного пути.

Опыт мореплавания подтверждает, что погрешности в счислении пути, когда ориентировка по берегу невозможна или затруднена, или ее пренебрегают, часто приводит к тяжелым последствиям, вплоть до гибели судна, особенно когда плавание осуществляется вблизи берегов и подводных опасностей. Естественно возникает необходимость периодически корректировать счисление по результатам измерений различных навигационных параметров.

Определение Места Судна (ОМС) при плавании вблизи берегов по визуальным или иным ориентирам с известными координатами и нанесенными на навигационную морскую карту, является необходимым условием обеспечения безопасности в современном судовождении.

Обсервация (ОМС) заключается в отыскании географических координат (j₀ и l₀) той точки, где в данный момент находится судно. Найденные путем обсервации координаты носят название обсервованных (j₀ и l₀).

Для определения обсервованных координат необходимо измерить как минимум два навигационных параметра.

Навигационные параметры подразделяются:

- пеленг ориентира,

- расстояние межу судном и ориентиром,

- разность расстояний, измеренных с судна до двух ориентиров,

- горизонтальный угол между двумя ориентирами,

- вертикальный угол (угловая высота) ориентира,

- высота небесного светила.

По методу измерения навигационного параметра получили и название способ обсервации:

Измерение пеленгов – по пеленгам ориентиров:

КК 95 (-5,0)

КК 95 (-5,0)

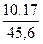
Рис. 60

Измерение расстояний – по расстояниям до береговых ориентиров:

Измерение горизонтальных углов – по двум горизонтальным углам,

Измерение угловой высота ориентира – по вертикальным углам,

Измерение разности расстояний между двумя ориентирами - по разности расстояний между ориентирами,

Измерение высота светила – по двум, четырем высотам небесных светил.

a b

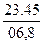
Более чаще обсервации подразделяются на:

- астрономические,

- навигационные:

- визуальные,

- с помощью радиотехнических средств.

Визуальные обсервации в свою очередь подразделяются:

- одновременные,

- по однородным ориентирам,

- по разнородным ориентирам,

- разновременные.

Счислимо - обсервованное место

Sл

Рис. 64

Необходимо всегда помнить, что счисление и обсервация – это непрерывный процесс решения основной задачи судовождения – обеспечение движения судна по выбранному маршруту. Во всех условиях плавания нельзя пренебрегать ни счислением, ни обсервациями, и следует использовать взаимный их анализ для контроля и повышения надежности судовождения.

Чрезвычайно важно положение в навигации: «считать себя ближе к опасности».

Измеренный навигационный параметр используется для получения навигационной изолинии.

Геометрическое место точек, отвечающее постоянному значению навигационного параметра, называется навигационной изолинией.

Навигационные параметры определяют следующие изолинии:

- визуальный пеленг – линию пеленга,

- расстояние до ориентира в пределах 30 миль – окружность,

- расстояние до ориентира за пределами 30 миль – изостадия,

- горизонтальный угол – изогона (окружность),

- вертикальный угол – окружность,

- разность расстояний – гипербола.

Пространство около каждого ориентира, нанесенного на навигационную карту, рассматривается как поле, характеризуемое изолиниями. Определение места судна сводится к нахождению точки пересечения изолиний от двух или более ориентиров.

На сравнительно небольших расстояниях, например, при визуальных обсервациях, изолинии прокладываются непосредственно на карте (выполняется графическое решение). При больших расстояниях, когда необходимо учитывать сфероидичность Земли, непосредственная прокладка изолинии на карте становится затруднительной. В этом случае отрезок изолинии заменяют прямой линией, касательной или секущей к изолинии в небольшой области около обсервованного места, такая прямая называется линией положения.

Впервые изолинию заменил линией положения американский капитан Томас Сомнер при астрономической обсервации.

Для получения обсервованного места по измеренным навигационным параметрам используются следующие способы:

1. Графический способ (прокладка). Это непосредственное графическое построение изолинии на морской навигационной карте. Это возможно, если изолинии имеют простую геометрическую форму – прямая, окружность (используемые приборы – компас, радиолокатор).

2. Картографический способ. Это получение места судна с помощью сеток изолиний, нанесенных на морскую навигационную карту картографической службой. Картографический способ получения места судна применяется при использовании гиперболический радионавигационных систем.

3. Таблично - графический способ. Это нахождение координат Линии Положения (ЛП) по таблицам, а затем нанесение, по выбранным координатам этих ЛП на карту, в пересечении которых и будет

обсервованное место судна.

4. Аналитический способ. Это получение координат места судна непосредственно из формул, по которым рассчитываются поправки к счислимым координатам.

5. Графоаналитический способ. Это определение места судна путем расчета параметров линии положения (переноса Dn и его направления t) и прокладка линии положения на карте или бумаге. Пересечение линий положения и дает обсервованное место судна.

Лоция

12.1. Навигационные карты

Для выбора пути движения судна на море и контроля его места, положения для мореплавателей издаются различные руководства для плавания и навигационные карты. На практике судоводитель повседневно сталкивается с морскими навигационными картами, поэтому необходимо знать основные сведения по картографии – науке о составлении, производстве и использовании карт и планов.

Содержание морских навигационных карт и планов должно способствовать безопасности мореплавания. На них показывают рельеф дна, навигационные опасности, навигационное оборудование и береговую черту с размещением различных объектов на побережье.

Географической картой называется уменьшенное, обобщенное изображение земной поверхности, полученное по определенному математическому закону. При составлении карт земную поверхность принимают за поверхность сфероида или шара.

В зависимости от приближения, принятого для характеристики формы Земли, введены два понятия о кратчайшем расстоянии между двумя точками. Если за форму Земли принят сфероид, то линию кратчайшего расстояния между двумя точками называют геодезической линией, если же форма Земли принята в более грубом приближении за шар, то линию кратчайшего расстояния между двумя точками называют дугой большого круга (ДБК). Следует подчеркнуть, что разность расстояний по геодезической линии и ДБК при длине дуги 3000 миль составляет всего 0,5 метра, но без учета природы этих линий нельзя решать многие задачи навигации. ДБК, или ее еще называют ортодромией, обращена выпуклостью к ближайшему полюсу и пересекает меридианы под разными углами. Для строгого следования по ДБК необходимо непрерывно изменять курс судна на малую величину, что требует сложных расчетов. Для удобства использования компаса предпочтительнее плавать по линии постоянного курса. Кривую на поверхности Земли, пересекающую все меридианы под одним и тем же углом, назвали локсодромией (в переводу с греческого «косой бег»). Расстояние между двумя точками по локсодромии не является кратчайшим, но эта линия чрезвычайно важна в навигации.

Проекция с простейшей зависимостью между географическими координатами j и l на сфероиде и прямоугольными координатами на плоскости выразится:

х = аj

у = аl.

Эта зависимость определяет проекцию Меркатора, применяемую для построения морских навигационных карт. Такая карта должна удовлетворять следующим требованиям:

- она должна быть равноугольной, т.е. углы, пеленги и курсы на карте не должны искажаться,

- линия пути судна, составляющая с меридианами постоянный угол, должна изображаться на проекции прямой линией. На карте в проекции Меркатора локсодромия является прямой линией.

Для построения карты в Меркаторской проекции проектируют изображение земных меридианов и параллелей на боковую поверхность воображаемого цилиндра, касающегося земной поверхности по экватору или секущего ее по равноудаленным от него параллелям. При этом ось цилиндра должна совпадать с осью вращения Земли. Развернув цилиндр по одной из образующих, получим нормальную цилиндрическую проекцию, где меридианы и параллели изображаются в виде прямых, составляя прямоугольную сетку.

На развернутом в плоскость цилиндре длина меридианов не изменится, а каждая параллель растянется и станет равной по длине экватору.

Принимая Землю за шар, обозначим радиус параллели а а^* через r, а радиус Земли через R. Угол а* О Q является широтой параллели аа*.

Р_N

R = R Cos j/ R = r Sec j.

Тогда отношение между

а b r а^* длиной экватора и длиной

параллели, в какой-либо

j широте, будет:

E O R Q 2pR = 2pr Sec j.

Следовательно, параллели,

растягиваясь до длины эквато-

ра будут изменяться пропорцио-

P_S нально Secj.

Рис.65Для сохранения второго условия

построения навигационной карты,

т.е. для сохранения равноугольности, необходимо и меридианы растянуть также пропорционально Sec j. Поскольку меридианы на меркаторской карте растянуты в каждой точке пропорционально Sec j, то изображение одной минуты дуги меридиана изменяется с переменой широты и по мере удаления от экватора непрерывно увеличивается.

Измеряя расстояние на морской карте, необходимо меркаторскую милю брать на боковой рамке карты в той же самой широте, где расположено измеренное расстояние.

Масштаб карты. Степень уменьшения перенесенных на карту действительных размеров фигур или линий земной поверхности называется масштабом. Масштаб характеризуется отношением длины линии на карте к длине той же линии на поверхности Земли. Различают числовой и линейный масштабы. Числовой масштаб представляет собой дробь, числитель которого единица. А знаменатель число, показывающее, сколько единиц длины на местности содержится в единице длины на карте. Например: М 1:200000 , это значит, что в 1 см между двумя точками на карте соответствует расстояние в 200000 см на местности, между этими же точками. Предельной точностью масштаба называют линейное расстояние на местности, соответствующее 0,2 мм на навигационной карте (предельное расстояние, различимое невооруженным глазом человека на бумаге).

12.2 Руководства для плавания

Кроме навигационных карт издаются различного ряда пособия - руководства для плавания. Это будут: лоции, огни и знаки, расписания радиопередач штормовых предупреждений и НАВАРЕА. В иностранных пособиях, кроме лоций, огней и туманных сигналов, издаются многотомные издания. Где можно найти информацию о системах донесений, лоцманском обслуживании, времени передач штормовых предупреждений, НАВАРЕА, и другой информации (ГМССБ, СРНС и другие РНС).

К руководствам для плавания относятся также и различные правила и руководства (Правила плавания каналами, документы по безопасности мореплавания, атласы ветров и течений и другое).

Лоция – это описание побережья и прибрежных вод, изложение рекомендаций для безопасного плавания вдоль берега и на подходах к портам.

Огни и знаки. В этой книге в табличной форме дано описание и характеристика светящих и несветящих навигационных знаков, установленных на берегу, и также навигационного ограждения, выставляемого на или вблизи опасности.

РТС НО. В этой книге в табличной форме приведены сведения о морских радиомаяках, аэромаяках, о различных радионавигационных системах, и радиолокационных маяках-ответчиках, устанавливаемых на береговых или плавучих сооружениях или знаках.

Расписание передач по радио навигационной и метеорологической информации, включает в себя время, частоту, район и объем информации, передаваемой по радио.

Правила. Такие правила: как правила плавания по Суэцкому и Панамскому каналам дают в полном объеме информацию по подготовке, проходу каналом и канальных сборах.

Таблицы приливом. В книгах в табличной форме приведены сведения о приливо-отливных явлениях в основных портах мира и дополнительная таблица с поправками приливных явлений к сведениям по основным портам для большинства мест мирового океана и побережий морских стран. Таблица переиздается ежегодно.

Для поддержания на уровне современности информации, содержащейся в навигационных пособиях и картах, установлена система для их корректуры. В 1980 году принята Международная система передачи навигационных предупреждений, для поддержания на уровне современности навигационных карт. В соответствие с этой системой весь мировой океан разделен на 16 районов. За каждым районом закреплен районный координатор, в обязанности которого входит сбор информации по своему району об изменениях навигационной обстановки, ее систематизация и передача по радио. В каждой морской стране имеется гидрографическая служба, в обязанности которой входит сбор и передача районному координатору наиболее важной навигационной информации об изменениях в навигационной обстановке. В тоже время гидрографическая служба ведает эксплуатацией и развитием ограждений навигационных опасно