Доказательство формулы размерности

Сформулируем вопрос: всегда ли формула размерности имеет вид степенного одночлена (6.1)? Оказывается всегда. Для доказательства этого утверждения проведем следующие расуждения. Пусть имеются, например, три исследователя 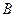, 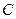и , и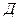зучающие одно и то же явление, но пользующиеся различными единицами измерения для физических параметров 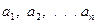, определяющих это явление:

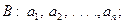
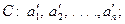
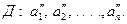
При этом положим, что масштабы единиц измерения у этих наблюдателей связаны между собой следующим образом:

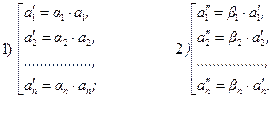
Тогда единицы измерения наблюдателя Д связаны с единицами измерения наблюдателя А формулами

.

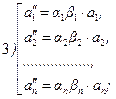Пусть все исследовател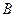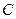и , и 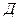измеряют одну и ту же физическую величину 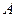и получают для нее из-за различия единиц измерения а₁, а₂,…а_nтри различные значения: А_В, А_Си А_Д.Пусть далее функция 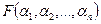переменных 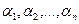показывает, во сколько раз изменяется значение 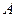, если единицы измерения 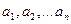наблюдателя изменить соответственно в 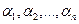раз. Тогда значения А_В, А_Си А_Ди должны быть связаны следующими формулами:

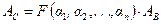
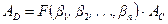
и, следовательно,

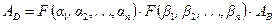(6.3)

С другой стороны (если перейти от единиц измерения первого наблюдателя к единицам измерения третьего наблюдателя), должно выполняться равенство

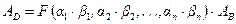. (6.4)

Поскольку физическая величина 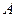не может зависеть от промежуточных систем единиц измерения, то функция 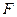должна удовлетворять следующему функциональному уравнению

,

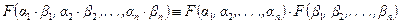которое получается путем сравнения равенств (6.3) и (6.4).

Не останавливаясь на деталях решения этого функционального уравнения, скажем, что существует единственная функция, ему удовлетворяющая:

,

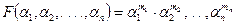где 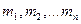— произвольные действительные числа [ ].

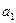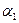Таким образом, при изменении единицы измерения в раз величина 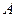меняется в 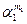раз, при изменении 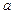₂ в 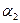раз величина 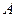меняется в 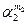раз и т.д. Значит, величина 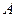имеет размерность

,

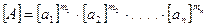что и доказывает формулу размерности (6.2).