Основной вопрос теории размерности

Пусть рассматривается физическое явление, математическая запись которого представляет собой зависимость определяемого параметра 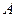от некоторых величин 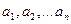, характеризующих это явление:

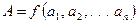. (6.5)

Заметим, что, с одной стороны, аргументы этой зависимости, в общем случае являются размерными величины, то есть их численные значения зависят от выбора система единиц измерени. Выбрав за исходную другую систему единиц, получим другие значения аргументов функции . Следовательно, за счет изменения системы единиц измерения, можно произвольно изменять численные значения аргументов функции ƒ.

С другой стороны, вид функции ƒ не должен зависеть от выбора системы единиц измерения, поскольку эта функция выражает физическую закономерность, не связанную с тем, какой наблюдатель ее изучает и какой системой единиц при этом пользуется. Значит должна существовать такая запись этой зависимости, которая не зависит от выбора единиц измерения, или, как говорят, инвариантна по отношению к нему. Ясно, что такая запись должна содержать только безразмерные величины.

Теорема, доказывающая возможность записи всякого соотношения между размерными величинами, выражающего физическую закономерность, в безразмерном инвариантном виде, была доказана Букингемом и называется 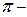теоремой.