Критерии подобия и техника моделирования
Установим необходимые и достаточные условия подобия двух явлений. Пусть явление состоит в том, что некоторая физическая величина А определяется рядом физических параметров 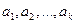 так, что
так, что
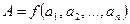 . (6.21)
. (6.21)
Рассматриваемая модель этого явления состоит в зависимости аналогичной физической величины 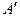 от тех же физических параметров, значения которых, однако,
от тех же физических параметров, значения которых, однако, 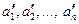 отличаются от значений параметров, определяющих величину A. Имеем
отличаются от значений параметров, определяющих величину A. Имеем
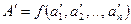 . (6.22)
. (6.22)
Согласно π-теореме обе зависимости (6.21) и (6.22) могут быть переписаны в безразмерном виде
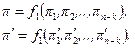 , (6.23)
, (6.23)
где k — число размерно-независимых параметров среди величин 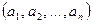 .
.
Равенства (6.23) показывают, что если параметры 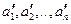 подобраны таким образом, что выполняются условия
подобраны таким образом, что выполняются условия
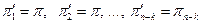 , (6.24)
, (6.24)
то будет также выполняться и условие
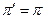 , (6.25)
, (6.25)
т.е. значение параметра A будет находиться по значению параметра 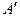 простым пересчетом
простым пересчетом
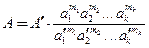 , (6.26).
, (6.26).
и, по определению, рассматриваемые явления будут подобны.
Таким образом, необходимым и достаточным условием подобия двух явлений будет условие равенства безразмерных комплексов, определяющих эти явления: условия (7.24). Поэтому безразмерные параметры 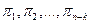 называют еще критериями подобия.
называют еще критериями подобия.
В качестве примера двух подобных явлений рассмотрим пример моделирования установившегося движения несжимаемой жидкости в трубе на установке, размеры которой уменьшены по сравнению с натурой.
В соответствии с формулой (6.15) эта зависимость имеет вид:
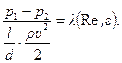
Обозначим посредством 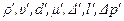 значения гидродинамических параметров течения, относящиеся к установке. Без индекса „штрих" эти величины относятся к моделируемому явлению. Тогда
значения гидродинамических параметров течения, относящиеся к установке. Без индекса „штрих" эти величины относятся к моделируемому явлению. Тогда
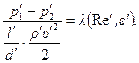
Ясно, что, выбрав параметры установки и режим движения жидкости так, чтобы выполнялись соотношения
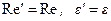 , (6.27)
, (6.27)
или
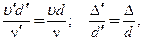
мы обеспечим равенство
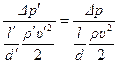
или
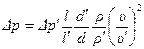 .
.
Если задаться отношением 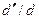 , показывающим, во сколько раз уменьшены размеры установки по сравнению с натурным объектом, а также - отношением вязкостей жидкости, текущей в натурной трубе и жидкости, применяемой для моделирования
, показывающим, во сколько раз уменьшены размеры установки по сравнению с натурным объектом, а также - отношением вязкостей жидкости, текущей в натурной трубе и жидкости, применяемой для моделирования 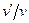 , то скорость движения жидкости в экспериментальной установке и шероховатость стенок установки, которые необходимы для подобия, будут определены соотношениями:
, то скорость движения жидкости в экспериментальной установке и шероховатость стенок установки, которые необходимы для подобия, будут определены соотношениями:
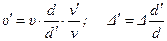 .
.
Формулы (6.27) показывают, что в рассматриваемом случае подобие обеспечивается соблюдением двух условий: равенства чисел Рейнольдса и относительной шероховатости на натуре и на модели. Поэтому число Рейнольдса и относительная шероховатость служат важными критериями подобия различных течений жидкости в трубе.
Дата добавления: 2016-05-16; просмотров: 602;
