Теоремы об эквивалентности пар сил.

1) действие пары на твердое тело не изменится, если ее перенести в любое место в плоскости ее действия (пару можно поворачивать в плоскости ее действия на любой угол).

Пара сил 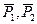с плечом d.

,

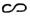
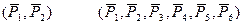т.к. ,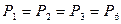

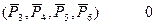
Получаем ,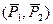

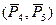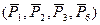т.к. 0

Суммы их направлены по диагонали ромба в противоположные стороны.

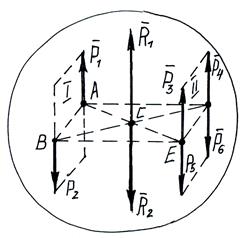2) Действие пары на твердое тело не изменяется, если перенести плоскость действия пары параллельно самой же.

Пара 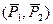лежит в плоскости I. Плоскость II параллельна плоскости I. АВ=DE. 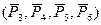0

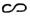
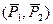
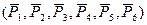
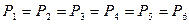
ABDE – параллелограмм, диагонали которого в т.С делятся пополам.

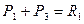
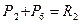
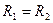уравновешиваются.

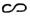Остается пара 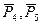, лежащая в плоскости II. Получаем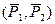

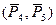
3) Действие пары на твердое тело не изменится, если изменить плечо и модули сил, сохраняя неизменным момент пары (пару можно поворачивать в плоскости ее действия на любой угол).

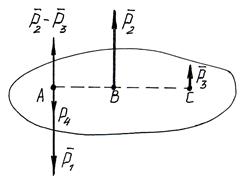
Разложим силу 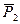на 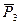(точка приложения т.С) и 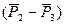. В т.А получим силу 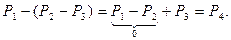Получим новую пару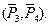

Рассмотрим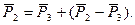

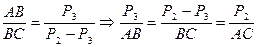, отсюда .

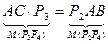Получили момент пары 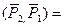моменту пары 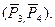Заметим, что момент пары равен моменту одной из сил относительно точки другой.

Следствие из 3 теорем:

1). Момент пары можно переносить в любую точку. Момент пары - свободный вектор.

2). Если моменты пар , равны, то пары эквивалентны.

СЛОЖЕНИЕ ПАР СИЛ.

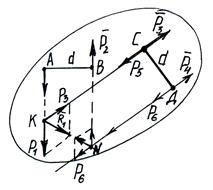
Система пар, действующих на твердое тело, эквивалентна одной паре, момент которой равен геометрической сумме моментов этих пар.

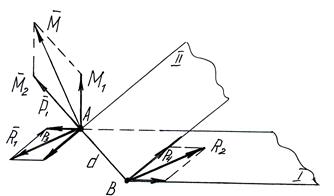Докажем это для 3 пар. Даны 2 пары сил с моментам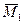и и 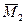, лежащие в плоскостях I и II.

АВ – прямая пересечения плоскостей I и II.

АВ=d

момент

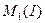
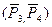момент .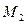

.

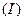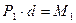
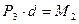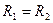
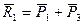
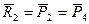пары 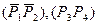заменяются одной парой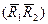

Найдем момент равнодействующий .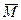

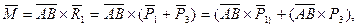
но 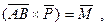а

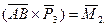
Следовательно:

Если n пар, то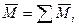

Если же пары лежат водной плоскости, то эта система пар эквивалентна паре, лежащей в той же плоскости и момент её равен алгебраической сумме моментов этих пар.