Главный вектор, главный момент.
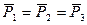 произвольно расположенные силы
произвольно расположенные силы
т. приложения 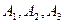 .
.
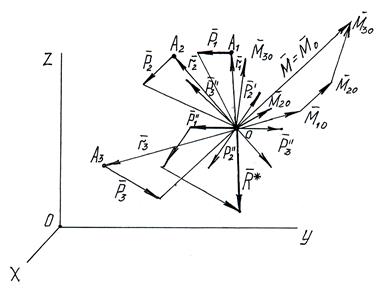
Приведём их к произвольному центру О.
Получим:
1). 3 силы 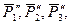 приложены в т.О;
приложены в т.О;
2). 3 приложенные пары
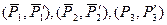 .
.
Складывая 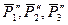 по правилу многоугольника, получим их равнодействующую
по правилу многоугольника, получим их равнодействующую 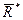 , равную их геометрической сумме.
, равную их геометрической сумме.
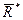
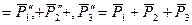
Геометрическая сумма всех сил системы называетсяглавным вектором системы сил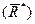 .
.
Складывая пары 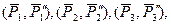 получим эквивалентную им пару. Момент каждой присоединенной пары сил равен моменту соответствующей силы относительно центра приведения О.
получим эквивалентную им пару. Момент каждой присоединенной пары сил равен моменту соответствующей силы относительно центра приведения О.
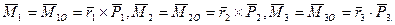
Момент эквивалентной пары равен геометрической сумме моментов присоединенных пар.
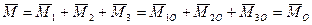
Момент 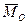 , равный геометрической сумме моментов сил данной системы относительно какой-либо точки, называется главным моментом системы сил относительно этой точки.
, равный геометрической сумме моментов сил данной системы относительно какой-либо точки, называется главным моментом системы сил относительно этой точки.
Распространяем полученные результаты на любое число сил:
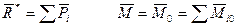
Силы, произвольно расположенные в пространстве, можно привести к одной силе, равной их главному вектору, и приложенной в центре приведения, и к паре сил, с моментом, равным главному моменту всех сил относительно центра приведения.
Выбор центра приведения не отражается на 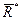 , но влияет на модуль и направление главного момента.
, но влияет на модуль и направление главного момента.
Дата добавления: 2017-02-04; просмотров: 749;
