Механика твердого тела
Момент инерции.
Моментом инерции материальной точки относительно оси вращения называется произведение массы этой точки на квадрат расстояния от оси:
Моментом инерции системы(тела) относительно оси вращения называется физическая величина, равная сумме произведений масс n и материальных точек системы на квадраты их расстояний до рассматриваемой оси.
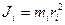
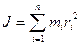
В случае непрерывного распределения масс эта сумма сводится к интегралу 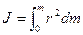 , где интегрирование производится по объему тела.
, где интегрирование производится по объему тела.
Главный момент инерции— момент инерции относительно главной оси вращения проходящей через центр масс
Момент инерции тела зависит от того, относительно какой оси оно вращается и как распределена масса тела по объему.
Моменты инерции однородных тел массой m, имеющих правильную геометрическую форму и равномерное распределение массы по объёму:
| Тело | Положение оси вращения | Момент инерции |
| Полый тонкостенный цилиндр радиуса R | Ось симметрии | 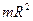
|
| Сплошной цилиндр или диск радиуса R | Ось симметрии | 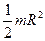
|
| Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его середину | 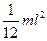
|
| Шар радиусом R | Ось проходит через центр шара | 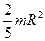
|
Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера:
Момент инерции тела J относительно произвольной оси z равен сумме момента его инерции 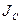 относительно параллельной оси, проходящей через центр масс С тела, и произведения массы да тела на квадрат расстояния a между осями:
относительно параллельной оси, проходящей через центр масс С тела, и произведения массы да тела на квадрат расстояния a между осями:
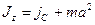
Например, момент инерции прямого тонкого стержня длиной l относительно оси, которая перпендикулярна стержню и проходит через его конец, (эта ось отстоит на l/2 от оси, проходящей через центр стержня):

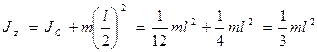
Таким образом величина момента инерции зависит от выбора оси вращения.
22.Кинетическая энергия вращения.
Абсолютно твердое тело вращается около неподвижной оси z проходящей через него. Все точки движутся с одинаковой угловой скоростью 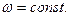 Кинетическая энергия тела:
Кинетическая энергия тела:
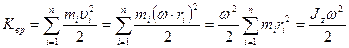
где 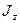 - момент инерции тела относительно оси z.
- момент инерции тела относительно оси z.
Если тело совершает поступательное и вращательное движения одновременно, то его полная кинетическая энергия равна сумме кинетических энергий:
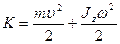
Из сопоставления формул кинетической энергии для поступательного и вращательного движений видно, что мерой инертности при вращательном движении служит момент инерции тела.
23. Момент силы.
Моментом силы 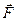 относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора
относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора 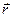 , проведенного из точки О в точку А приложения силы, на силу
, проведенного из точки О в точку А приложения силы, на силу 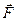 :
:
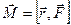
|
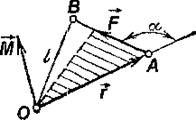
Модуль момента силы: 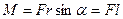 ,где
,где 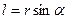 — плечо силы— кратчайшее расстояние между линией действия силы и точкой
— плечо силы— кратчайшее расстояние между линией действия силы и точкой
О; α — угол между 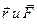 .
.
Моментом силы относительно неподвижной оси z — называется скалярная величина 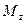 , равная проекции на эту ось вектора
, равная проекции на эту ось вектора 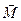 момента силы, определенного относительно произвольной точки Оданной оси z. Значение момента не зависит от выбора положения точки О на оси z.
момента силы, определенного относительно произвольной точки Оданной оси z. Значение момента не зависит от выбора положения точки О на оси z.
24.Основное уравнение динамики вращательного движения твердого
Тела.
При повороте тела под действием силы 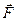 на бесконечно малый угол
на бесконечно малый угол 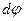 точка приложения силы А проходит путь
точка приложения силы А проходит путь 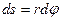 и работа равна:
и работа равна:

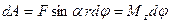
Работа вращения тела идет на увеличение его кинетической энергии:
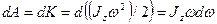
Тогда 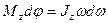 , или
, или 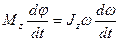 откуда
откуда
уравнение динамики вращательного движения твердого тела:
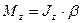
Если ось вращения совпадает с главной осью инерции, проходящей через центр масс, то имеет место векторное равенство:
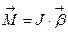
где J — главный момент инерции тела(момент инерции относительно главной оси).
25. Момент импульса и закон его сохранения.
Моментом импульса(количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:
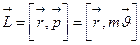
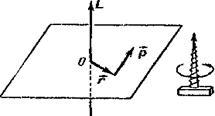
Моментом импульса относительно неподвижной оси z называется скалярная величина 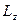 , равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Значение момента импульса
, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Значение момента импульса 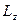 , не зависит от положения точки О на оси z.
, не зависит от положения точки О на оси z.
При вращении абсолютно твердого тела вокруг неподвижной оси каждая точка тела движется по окружности постоянного радиуса 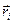 со скоростью
со скоростью 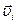 перпендикулярной радиусу. Момент импульса отдельной частицы равен
перпендикулярной радиусу. Момент импульса отдельной частицы равен 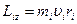 и направлен по оси в сторону, определяемую правилом правого винта (совпадает с направлением вектора угловой скорости
и направлен по оси в сторону, определяемую правилом правого винта (совпадает с направлением вектора угловой скорости 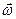 ).
).
Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:
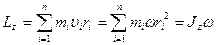
Продифференцируем по времени: 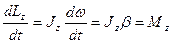
В векторной форме: 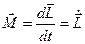 - ещё одна форма уравнения динамики вращательного движения твердого тела.
- ещё одна форма уравнения динамики вращательного движения твердого тела.
В замкнутой системе момент внешних сил 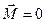
 , следовательно и
, следовательно и 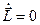 .
.
Закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени:
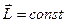
Это — фундаментальный закон природы. Он является следствием изотропности пространства: инвариантность физических законов относительно выбора направления осей координат системы отсчета.
При равномерном вращении твердого тела относительно некоторой оси z закон сохранения момента импульса 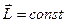 равносилен:
равносилен: 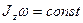 .
.
26.Сопоставим основные величины и соотношения для поступательного движения тела и для его вращения вокруг неподвижной оси.
| Поступательное движение | Вращательное движение | ||
| Масса | т | Момент инерции | J |
| Перемещение | 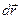
| Угловое перемещение | 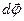
|
| Скорость | 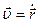
| Угловая скорость | 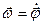
|
| Ускорение | 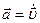
| Угловое ускорение | 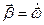
|
| Сила | 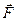
| Момент силы | 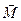
|
| Импульс | 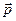
| Момент импульса | 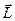
|
| Работа | 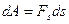
| Работа | 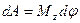
|
| Кинетическая энергия | 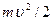
| Кинетическая энергия | 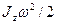
|
| Основное уравнение динамики | 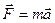
| Основное уравнение динамики | 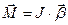
|
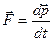
| 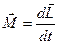
|
Дата добавления: 2016-04-22; просмотров: 2433;
