ЗАКОНЫ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ

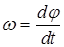Вращательное движение материальной точки характеризуется следующими величинами : углом поворота , угловой скоростью и угловым ускорением .

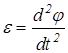При вращательном движении результат действия сил на тело определяется действующим на него моментом силы М и зависит от момента инерции J тела. Произведение момента инерции тела на его угловое ускорение численно равно результирующему моменту сил, действующих на это тело :

M= e J . (1)

Cоотношение (1) называется основным уравнением динамики вращательного движения.

Моментом силы относительно оси называется вектор, направленный вдоль оси, численно равный произведению силы на плечо, если сила действует в плоскости, перпендикулярной оси вращения.

Моментом инерции J материальной точки относительно оси вращения называется произведение массы m точки на квадрат расстояния r до оси вращения

J=mr² . (2)

Момент инерции любого тела равен сумме моментов инерции составляющих его материальных точек

J= , (3)

где N - число частиц, на которое разбито тело; m_i и r_i - масса и расстояние от точки до оси вращения.

Момент инерции тел во воащательном движении выполняет роль, аналогичную роли массы в поступательном движении. Как масса, так и момент инерции являются мерой инертности .

Для однородных тел простой формы момент инерции относительно оси симметрии может быть рассчитан аналитически. Например, момент инерции плоского диска или сплошного цилиндра относительно геометрической оси симметрии равен

J= ,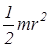

где m - масса диска или цилиндра, r - радиус диска или цилиндра.

Момент инерции шара относительно оси, совпадающей с любым из его диаметров, вычисляется так:

J= ,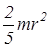

где m и r - масса и радиус шара.

Момент инерции тела относительно любой оси может быть рассчитан по теореме Штейнера, которая формулируется следующим образом : момент инерции J тела относительно произвольной оси равен сумме момента инерции J₀ этого тела относительно оси, проходящей через центр тяжести параллельно данной оси, и произведения массы тела m на квадрат расстояния d между осями :

J=J₀+md² .

(4)

Кинетическая энергия вращающегося относительно неподвижой оси тела также зависит от момента инерции его :

W_кин= .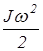

(5)

Работа при вращении твердого тела равна

А=М ,

(6)

где М - вращающий момент силы, - угол поворота под действием момента М.

Когда во время движения тела момент инерции его изменяется, основное уравнение динамики вращательного движения должно быть записано в более общей форме:

. (7)

Величина J называется моментом количества движения. Из уравнения (7) как следствие вытекает закон сохранения момента количества движения. Если суммарный момент, действующий на тело или систему тел, равен нулю, то момент количества движения этого тела или системы тел остается неизменным, т.е. если М=0, то L= const.

При сложной геометрической форме тела аналитический подсчет его момента инерции провести трудно. В этих случаях его определяют экспериментально.