ДЕФОРМАЦИИ ТВЕРДОГО ТЕЛА

Деформация тел - изменение их размеров и формы - происходит под действием сил, приложенных к данным телам.

Деформация называется упругой, если она исчезает после прекращения действия силы, и пластической, если она сохраняется и после снятия нагрузки.

Величина, равная отношению силы к площади поверхности, на которую сила действует, называется напряжением или усилием. Благодаря взаимодействию частей тела друг с другом напряжение передается во все точки тела, т.е. весь его объем оказывается в напряженном состоянии. Если сила F_n направлена по нормали (т.е. перпендикулярно) к поверхности, то напряжение называется нормальным и обозначается буквой σ:

(1)

Если сила F_t направлена по касательной к поверхности, то напряжение называется тангенциальным и обозначается буквой τ:

(2)

Все возможные виды упругих деформаций твердого тела могут быть сведены к двум основным: растяжение (или сжатие), возникающие при нормальных напряжениях, и сдвиг под действием касательных напряжений.

Деформация растяжения. Деформация растяжения возникает под действием сил F_n, направленных по нормали к той поверхности, к которой они приложены.

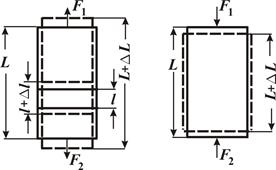
Если к концам однородного стержня постоянного сечения приложить направленные вдоль его оси силы F₁и F₂ (F₁ = F₂ =F_n), действие которых равномерно распределено по всему сечению, то длина стержня L получит положительное (при растяжении) или отрицательное (при сжатии) приращение ΔL (рис. 1). При этом каждый произвольно выбранный элемент стержня l получает приращение Δl, пропорциональное его длине, так что для всех элементов стержня отношение Δl / l оказывается одинаковым. Следовательно, в качестве величины, характеризующей деформацию стержня, можно взять его относительное удлинение:

	(3)
Рис. 1

Из (3) видно, что ε - безразмерная величина. В случае растяжения ε > 0, в случае сжатия ε < 0. Из опыта известно, что относительное удлинение при упругой деформации пропорционально силе, приходящейся на единицу площади поперечного сечения стержня:

,

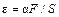(4)

где α называется коэффициентом упругости и зависит только от свойств материала стержня.

Воспользовавшись данным выше определением нормального напряжения (1), выражение (4) можно записать:

(5)

т. е. относительное удлинение пропорционально нормальному напряжению.

Для характеристики упругих свойств материала наряду с коэффициентом упругости α пользуются обратной ему величиной, которая называется модулем Юнга:

(6)

Таким образом, выражение (5) принимает вид

(7)

Отсюда следует, что модуль Юнга равен такому нормальному напряжению, при котором относительное удлинение ε было бы равно единице (т.е. приращение длины ΔL, было бы равно первоначальной длине).

С учетом (1) и (3) соотношение (7) может быть приведено к следующему виду:

(8)

где k - постоянный для данного стержня коэффициент.

Согласно выражению (8) удлинение стержня при упругой деформации пропорционально действующей на стержень силе. Это соотношение выражает закон Гука для данной деформации. Этот закон выполняется только до тех пор, пока не достигается предел упругости.

Деформация сдвига. Деформация сдвига возникает под влиянием сил F_t, касательных к той поверхности, на которую они действуют. Под влиянием этих сил происходит параллельный сдвиг одного слоя тела относительно другого. Любая прямая, проходящая вначале перпендикулярно к слоям, после их сдвига окажется повернутой на некоторый угол ψ (рис. 2).

		При малом значении угла ψ приближенно имеем 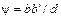, (9) где d - толщина тела, bb' -абсолютная величина сдвига верхнего слоя относительно нижнего. Угол сдвига ψ характеризует относительный сдвиг слоев, и в пределах применимости закона Гука можно написать
	Рис. 2
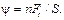
	(10)

Используя определение тангенциального напряжения (2), получаем:

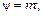
(11)

т.е. угол сдвига будет прямо пропорционален приложенному к телу усилию. Постоянная величина n, зависящая от материала тела, называется коэффициентом сдвига. Величина G, обратная коэффициенту сдвига, называется модулем сдвига

(12)

 

Если угол ψ равен одному радиану, то G = τ , т.е. в пределах упругости модуль сдвига численно равен касательному усилию, вызывающему угол сдвига, равный одному радиану.

Деформация сдвига имеет место, например, при закручивании однородного круглого стержня. Если один конец круглого стержня закрепить неподвижно, а к другому приложить вращательный момент, то одно основание стержня повернется вокруг оси стержня на некоторый угол относительно другого основания. Легко видеть, что деформация при кручении представляет собой деформацию сдвига. Действительно, если разбить стержень на элементарные коаксиальные слои, то закручивание приведет к сдвигу каждого из таких слоев по отношению к соседним с ним слоям.

Можно показать [2], произведя расчет, что угол закручивания цилиндрического стержня будет определяться следующим выражением:

(13)

где L - длина стержня, r - радиус стержня, M - момент силы, действующей на стержень, G - модуль сдвига. Обозначив величину

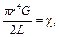
(14)

имеем

(15)

Это соотношение выражает закон Гука при кручении. Величину χ называют модулем кручения, в отличие от модуля сдвига. Она характеризует конкретный стержень и зависит от его размеров [1].

 

---

Дата добавления: 2016-04-19; просмотров: 2163;

---