ДЕФОРМАЦИИ ПРИ ИЗГИБЕ.
Графоаналитический метод определения деформации балок.
Действительные балки
 y' = 0; y = 0
y' = 0; y = 0
| Фиктивные балки

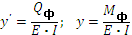
|

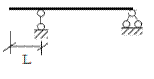
| 
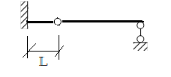
|
Порядок расчета рассмотрим на примере.
Пример 1. Определить прогиб y, и угол поворота y' в свободном конце балки.
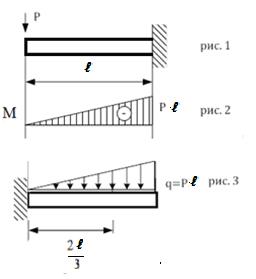
| Порядок расчета:
1. Стоят эпюру М от внешней нагрузки (см рис 2).
2. Загружают фиктивную балку нагрузкой в виде
эпюры М (рис.3)
3. Вычисляем фиктивную поперечную силу (Qф) и фиктивный момент (Мф) в том сечении фиктивной балки, где требуется определить y и y' (т.е. в защемлении фиктивной балки)
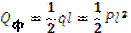
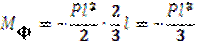 4. Прогиб и угол поворота равны:
4. Прогиб и угол поворота равны:
|

Определение деформации балок методом начальных параметров.
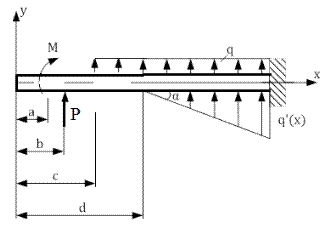
| Правило знаков: Нагрузки, действующие согласно рисунку считаются положительными. . |
Формулы метода начальных параметров:
Прогиб:
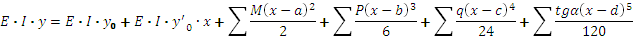
Угол поворота:
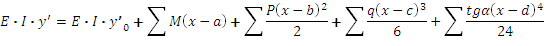
Где a, b, c, d- расстояния от начала координат до момента М, силы Р, нагрузки q, или начало неравномерно-распределенной нагрузки q(x).
y0 и y0' - это прогиб и угол поворота в начале координат.
Примечание:
1. Если распределенная нагрузка не доходит до рассматриваемого сечения, то её продлевают до конца балки (показана штриховой линией).
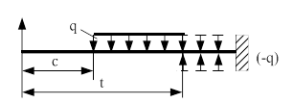
Одновременно по этим участкам прикладываем такую же нагрузку с обратным знаком. Эту нагрузку надо учесть в формуле:
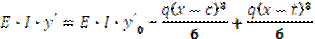
Аналогично поступают и при неравномерно распределенной нагрузке:
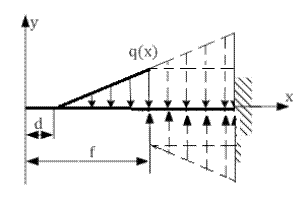
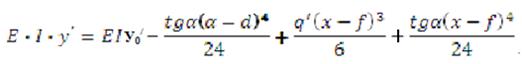
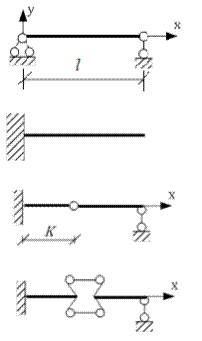
Граничные условия для балок:
|
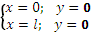 .
.
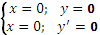
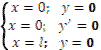
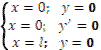
|
Определение перемещение методом Максвелла – Мора
Этот метод расчета был введен Максвеллом в 1864г. А в 1874г ввел практику расчетов Мор.
Угол поворота и прогиб балки можно определить по формуле Максвелла-Мора:
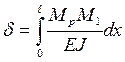
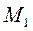 - усилие, вызванное единичной нагрузкой.
- усилие, вызванное единичной нагрузкой.
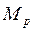 - изгибающий момент от заданной нагрузки.
- изгибающий момент от заданной нагрузки.
1) Если надо найти угол поворота, то в качестве единичной нагрузки является момент М1 =1.
2) При определении прогиба единичной нагрузкой является сосредоточенная сила Р1=1.
Примечание: если нагрузка делит балку на определенные участки, то этот интеграл делится на отдельные интегралы и суммируется
Пример 1. Определить прогиб в свободном конце балки.
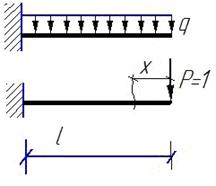
| 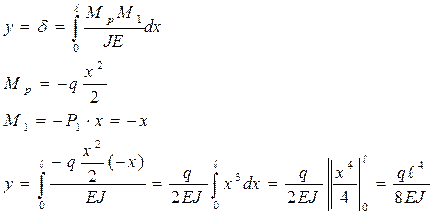 Ответ: «+» значит что направление прогибов совпадает с направлением единичной силы. Ответ: «+» значит что направление прогибов совпадает с направлением единичной силы.
|
Если элемент представляет собой брус малой кривизны, то перемещения определяем по формуле Мора.
Пример 2.Определить угол поворота свободного конца балки.
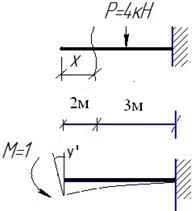
| 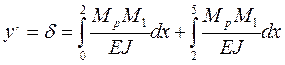 I участок
I участок 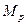 =0; =0; 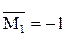 .
II участок .
II участок 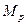 = -Р (х-2); = -Р (х-2); 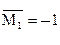 . .
|
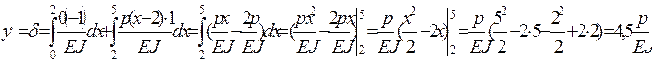
Если в расчете учитывать и поперечную силу, то пользуются формулой
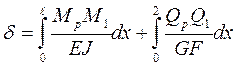
Пример 3.
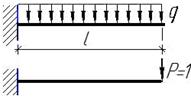
| Определить прогиб с учетом поперечной силы.
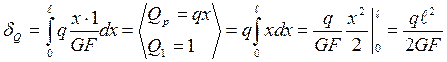 Окончательный прогиб ( см. пример №1):
Окончательный прогиб ( см. пример №1):
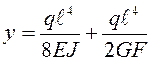
|
Примечания:
1.Расчеты показывают, что поперечная сила существенного влияния на деформации не оказывает.
2. Влияние поперечной силы учитываются только в расчете коротких балок.
| <== предыдущая лекция | | | следующая лекция ==> |
| Прямоугольное сечение. | | | Нулевая линия делит сечение на две части: на одной стороне, возникают сжимающие напряжения, а на другой растягивающие. |
Дата добавления: 2016-02-13; просмотров: 2360;
