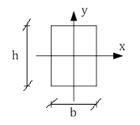
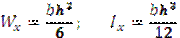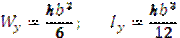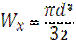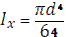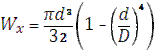Прямоугольное сечение.
|
|
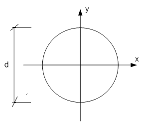
Круглое сечение.
|
|
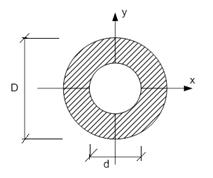
Кольцевое сечение.
|
|
Расчет балок на прочность.
Расчет по допускаемым напряжениям на прочность при изгибе.
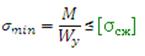
|
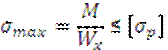
|
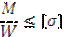
| – при симметричном сечении |
Проверка прочности по предельным состояниям.
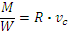
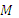 – максимальный изгибающий момент от расчетных нагрузок.
– максимальный изгибающий момент от расчетных нагрузок.
Рр=Рн×n
n – коэффициент перегрузки.
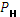 – нормативная нагрузка.
– нормативная нагрузка.
Рр – расчетная нагрузка.
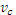 – коэффициент условия работы.
– коэффициент условия работы.
Если материал работает неодинаково на растяжение и сжатие, то прочность проверяется по формулам:
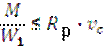
| 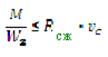
|
где Rp и Rсж – расчетное сопротивление на растяжение и сжатие
Расчет по несущей способности и учетом пластической деформации.
В предыдущих методах расчета прочность проверяется по максимальны напряжениям в верхних и нижних волокнах балки. При этом средние волокна оказываются недогруженными.
Оказывается, если нагрузку увеличивать дальше, то в крайних волокнах напряжение дойдет до предела текучести σт ( в пластичных материалах), и до предела прочности σnч ( в хрупких материалах). При дальнейшем увеличении нагрузки хрупкие материалы разрушатся, а в пластичных материалах напряжения в крайних волокнах далее не возрастают, а растут во внутренних волокнах. (см. рис.)
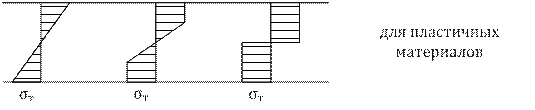
Несущая способность балки исчерпывается, когда по всему сечению напряжения достигнут σт.
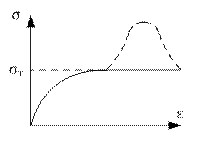
| W пл= S1+S2
W пл – пластический момент сопротивления
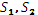 - статический момент растянутой и сжатой зон относительно нейтральной оси.
Мпред = σт × W пл - статический момент растянутой и сжатой зон относительно нейтральной оси.
Мпред = σт × W пл
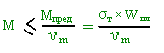 где где 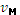 – коэффициент надежности по материалу. – коэффициент надежности по материалу.
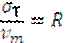 где R - расчетное сопротивление. где R - расчетное сопротивление.
| ||
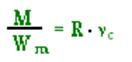
| - проверка прочности. | ||
Для прямоугольного сечения:
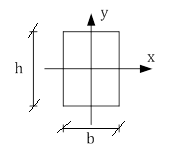
| 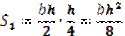
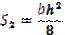 W пл=S1+S2=bh2 /4
W пл=bh2 /4 - для прямоугольного сечения.
W =bh2 /6 – обычный момент сопротивления.
W пл=1,5W
W пл=S1+S2=bh2 /4
W пл=bh2 /4 - для прямоугольного сечения.
W =bh2 /6 – обычный момент сопротивления.
W пл=1,5W
|
Примечание: для прокатных профилей (швеллер и двутавр) пластический момент Wnл=(1.1÷1,17)×W
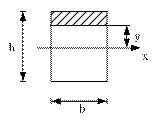
Касательные напряжения при изгибе балки прямоугольного сечения. Формула Журавcкого.
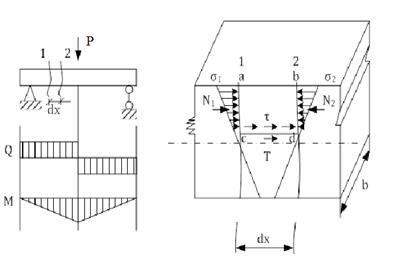
Так как момент в сечении 2 больше момента в сечении 1, то напряжение σ2>σ1=>N2>N1.
В этом случае элемент abcd должен переместиться влево. Этому перемещению препятствуют касательные напряжения τ на площадке cd.
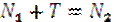 - уравнение равновесия, после преобразования которого получается формула для определения τ:
- уравнение равновесия, после преобразования которого получается формула для определения τ:  - Формула Журавского
- Формула Журавского
| где Q - поперечная сила, Sотс - статический момент отсеченной части относительно нейтральной оси, J-момент инерции всего сечения относительно нейтральной оси, b - ширина балки на уровне y. |
Распределение касательных напряжений в балках прямоугольного, круглого и двутаврового сечений.
1. Прямоугольное сечение:
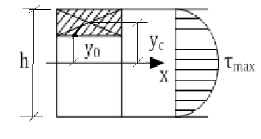
|
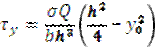 - формула для сечения на расстоянии у0 от нейтральной оси. - формула для сечения на расстоянии у0 от нейтральной оси.
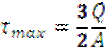
|
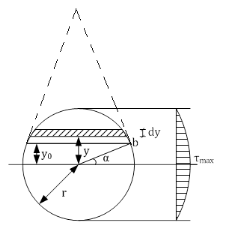
2.Круглое сечение.
|
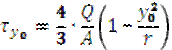 - формула для сечения на расстоянии у0 от нейтральной оси. - формула для сечения на расстоянии у0 от нейтральной оси.
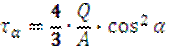 - формула для сечения под углом α. - формула для сечения под углом α.
|
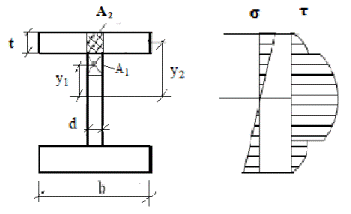
3. Двутавровое сечение.
|
Для стенки двутавра
касательные напряжения
вычисляют по формуле:
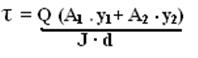
| |||
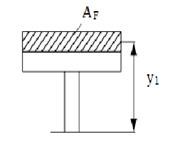
| Для полки: условно вертикальные касательные напряжения определяют по формуле:
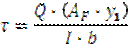
| |||
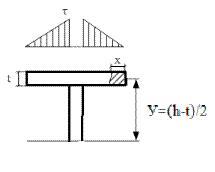
| В полках двутавров возникают касательные напряжения, направленные горизонтально:
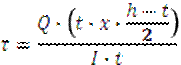
| |||
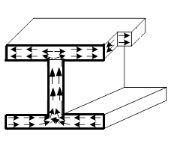
| На рисунке показан общий характер распределения τ в сечении двутавра. | |||
Главные напряжения при изгибе. Проверка прочности балок.
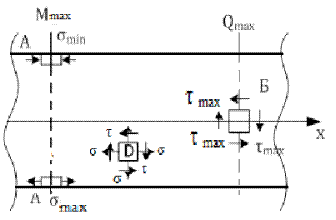
| Выделим из балки участок, на который действует максимально поперечная сила Qmax и изгибающий момент Mmax. Наиболее опасными точками являются сечение A и точка Б. Прочность проверяется по напряжениям в этих точках. На практике обычно ограничиваются проверкой сечения A: |
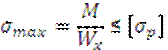
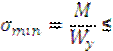 [σсж]
[σсж]
Примечание: при расчете по предельным состояниям вместо [σсж] и [σр] в формулы ставятся Rcж и Rp – расчетные сопротивления материала при сжатии и растяжении.
Если же балка короткая, то проверяют точку Б:
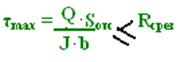 где Rсрез – расчетное сопротивление материала на срез.
где Rсрез – расчетное сопротивление материала на срез.
В точке D на элемент действует нормальные и касательные напряжения, поэтому в некоторых случаях их совместное действие вызывает опасность для прочности. В этом случае элемент D проверяют на прочность используя главные напряжения.
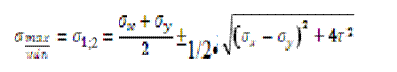
В нашем случае:  , следовательно:
, следовательно:
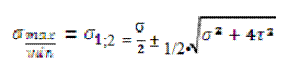
Используя σ 1 и σ2 по теории прочности проверяют элемент D.
По теории наибольших касательных напряжений имеем: σ 1 - σ2≤R
Примечание: точку D следует брать по длине балки там, где одновременно действуют большие M и Q.
По высоте балки выбираем такое место, где одновременно действуют значения σ и τ.
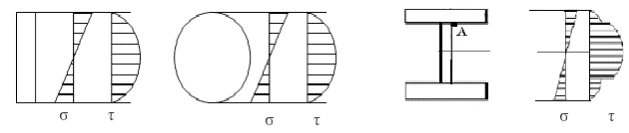
Из эпюр видно:
1. В балках прямоугольного и круглого сечения отсутствуют точки, в которых одновременно действуют большие σ и τ. Поэтому в таких балках проверка точки D не делается.
2. В балках двутаврового сечения на границе пересечения полки со стенкой (т. А) одновременно действуют большие σ и τ. Поэтому они проверяются на прочность в этой точке.
Примечание:
a) В прокатных двутаврах и швеллерах в зоне пересечения полки со стенкой сделаны плавные переходы (закругления). Стенка и полка подобраны так, что точка A оказывается в благоприятных условиях работы и проверка прочности не требуется.
b) В составных (сварных) двутавровых балках проверка точки А необходима.
Дата добавления: 2016-02-13; просмотров: 8909;