Контроль правильности построения эпюр Q и M
1) Если поперечная сила положительная Q>0, то эпюра M имеет вниз сходящую линию (см. пример 1)
2) Если Q – отрицательная (Q<0), то эпюра М на этом участке имеет восходящую линию.
3) Если Q меняет знак с «+» на «-», то эпюра М меняет также направление (М имеет Мmax в этой точке)
4) Если Q меняет знак с «-» на «+», то M имеет значение Mmin ( см. пример 2).
5) Под сосредоточенными силами на эпюре Q имеем скачок равный величине силы, а на эпюре М – перелом.
6) Под моментом на эпюре М имеем скачок на величину момента.
7) На участках нагруженных равномерно распределенной нагрузкой на эпюре Q имеем прямую наклонную линию, а на эпюре М – параболическую кривую ( см. пример 2) выгнутую в сторону действия нагрузки q.
8) На участках нагруженных неравномерно распределенной нагрузкой эпюры Q и М очерчены кривыми линиями.
Эпюры внутренних усилий для стержней ломаного и искривленного очертаний
Пример №1: Построить эпюры Q, N, M для плоской рамы.
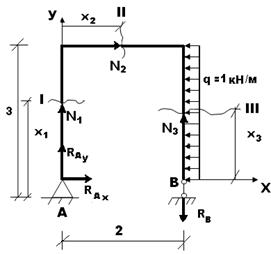
| 1) Находим опорные реакции
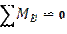
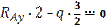
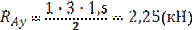
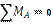
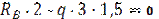
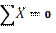
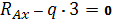
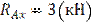
|
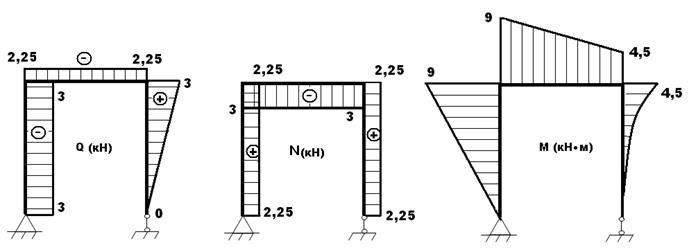
2) Построение эпюр Q, N, M.
В ломанных стержнях кроме Q и М возникают продольные силы N. Изгибающие моменты будем откладывать в сторону растянутых волокон (без указания знака)
Участок I:
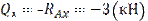
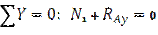
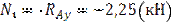
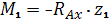
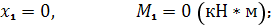
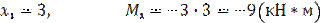
Участок II:
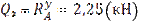
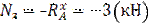
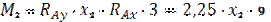
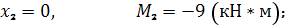
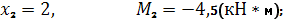
Участок III:
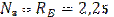
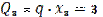





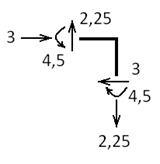
Проверка узла №1:
1) Прикладываем к узлу усилия, показанные на эпюрах.
2) Внешние моменты тоже прикладываем к узлу(если имеются).
3) Составляем уравнения равновесия узла. Если уравнения равны нулю, то узлы находятся в равновесии.
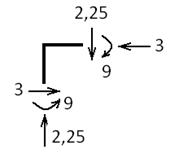 Проверка узла №2:
Проверка узла №2:
|
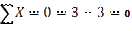
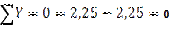
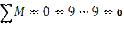 ∑Х=3-3=0
∑У=2,25-2,25=0
∑М=4,5-4,5=0
∑Х=3-3=0
∑У=2,25-2,25=0
∑М=4,5-4,5=0
|
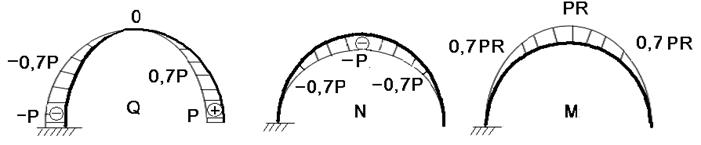
Пример №2.Построить эпюры Q, N, M для арки.
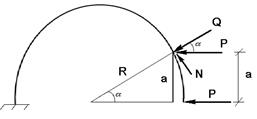
| 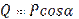
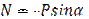
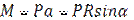 1)
1) 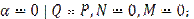 2)
2) 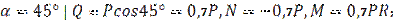 3)
3) 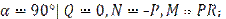 4)
4) 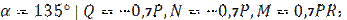
|
Определение нормальных напряжений при изгибе балки. Формула Новье.
Рассмотрим участок балки, работающей на чистый изгиб.
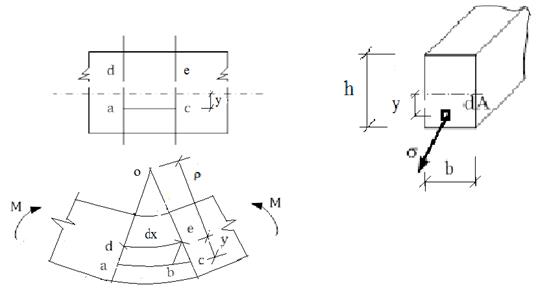
dx – начальная длина волокна, bc – удлиннение. волокна (а с)
 – радиус кривизны, 1/ρ– кривизна балки
– радиус кривизны, 1/ρ– кривизна балки
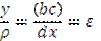 – относительное удлинение
– относительное удлинение
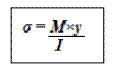
| - Формула Новье. По ней определяются нормальные напряжения в сечении балки. y – расстояние от нейтрального волокна до точки, где определяется напряжение. I – момент инерции, относительно нейтральной оси. | ||
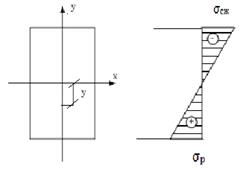
| при y = 0; σ= 0 при y = max; σ = max | ||
Понятие о моменте сопротивления.
|
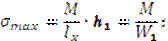
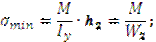
|
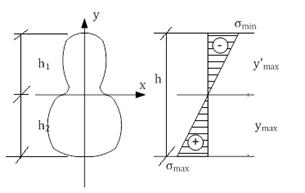
Момент сопротивления.
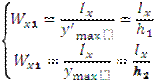 где ymax – расстояние от нейтральной оси до наиболее удаленного волокна.
где ymax – расстояние от нейтральной оси до наиболее удаленного волокна.
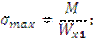
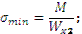
Моменты сопротивления некоторых простых фигур:
Дата добавления: 2016-02-13; просмотров: 2379;
