ИЗГИБ. ПОНЯТИЕ ОБ ИЗГИБЕ.
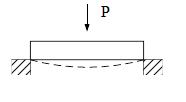
Деформация изгиба возникает под воздействием нагрузок, действующих перпендикулярных к оси стрежня, а так же пар сил, действующих в плоскости, проходящей через ось стержня.
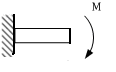
При изибе в поперечном сечении стержня возникают внутренние усилия: Q – поперечная сила, M - изгибающий момент.
Иногда в поперечном сечении стержня возникает только изгибающий момент - это чистый изгиб.
Стрежни, работающие преимущественно на изгиб называются балками.
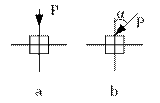
Если плоскость действия нагрузок совпадает с главной осью поперечного сечения, то такой изгиб называется прямым или плоским изгибом (см. рис. а) а если не проходит по главной оси поперечного сечения, то изгиб называется косым (см. рис. б).
Нанесем на боковой поверхности призматического стержня вертикальные линии и будем изгибать балку моментом М.
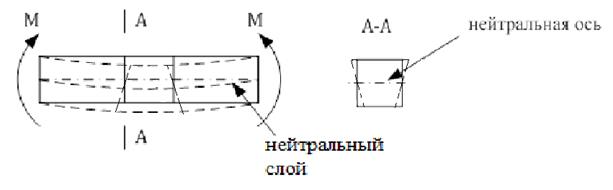
В результате деформации замечаем:
1) Плоское сечение до деформации остается плоским и после деформации (т.е. поперечное сечение не искривляется).
2) Расстояние между вертикальными линиями в верхней зоне балки уменьшается, а в нижней увеличивается, следовательно в верхней части возникает сжимающее напряжение, а в нижней растягивающие.
3) Поперечное сечение в верхней части увеличивается, а в нижней уменьшается.
Слой, где отсутствует нормальное напряжение называется нейтральным слоем, а пересечение нейтрального слоя с поперечным сечением называется нейтральной осью.
Опоры и опорные реакции.
1. Шарнирно-подвижная опора ( в ней возникает только вертикальная реакция)

2.Шарнирно-неподвижная опора.
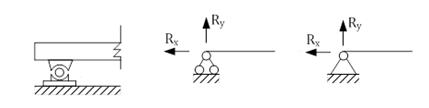
В шарнирно-подвижной опоре возникает две реакции вертикальная и горизонтальная.
Примечание: направлять реакции можно в любую сторону (вверх, вниз, вправо, влево)
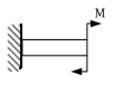
3. Жесткая заделка ( защемление)
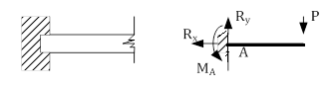
Жесткая заделка препятствует линейным и угловым перемещениям. В ней возникают три реакции ( изгибающий момент МА, вертикальная Ry и горизонтальная Rx реакции.
4.Неполное защемление (вертикальная реакция и изгибающий момент)
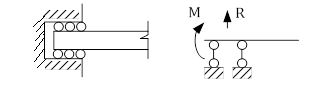
Статически определимые балки
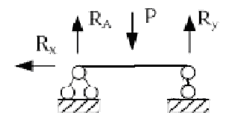 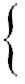 Неизвестных реакций n=3
Неизвестных реакций n=3
|
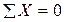
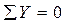 ∑Мизг=0
уравнения статики у=3
∑Мизг=0
уравнения статики у=3
|
Если число неизвестных n равно числу уравнений статики y, то система называется статически определимой. Неизвестные опорные реакции можно определить с помощью уравнений статики.
Статически неопределимые балки.
Если число неизвестных n больше числа уравнений статики, то это статически неопределимые балки.
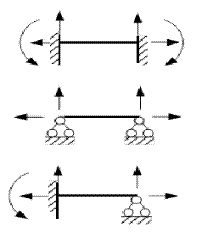
| n = 6 y = 3 л = n – y = 6 – 3 = 3 ( трижды статические неопределимая система л – число лишних связей n = 4 y = 3 л = 4 – 3 = 1 ( один раз статически неопределимая система) n = 5 y = 3 л = 5 – 3 = 2 (дважды статически неопределимая система) |
Вычисление опорных реакции.
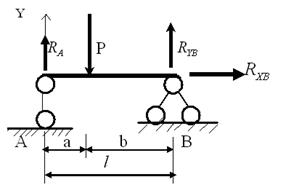
 Пример 1.Определить опорные реакции.Составим уравнения равновесия:
Пример 1.Определить опорные реакции.Составим уравнения равновесия:
|
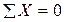 (1) (1)
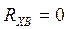
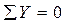 (2) (2)
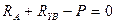
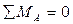 (3) (3)
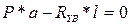
|

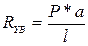 - подставим в (2):
- подставим в (2): 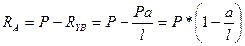 ;
;
Проверка: 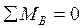 :
: 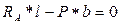 :
: 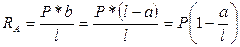
Пример 2.
 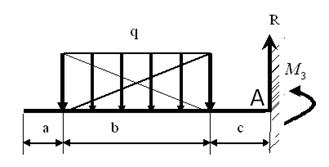
| 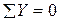
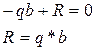 ∑МА=0
∑МА=0 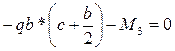 ; ;
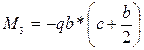 ; ;
|
Знак «-» показывает, что действительное направление реакции не совпадает с принятым.
Поперечная сила и изгибающий момент.
В поперечных сечениях балки возникает поперечная сила Q и изгибающий момент M.
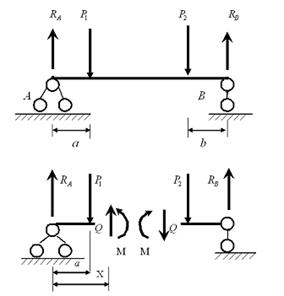
| Разрежем балку на расстоянии Х. Заменим действие отброшенной части (правой) внутренними усилиями Q и M; рассмотрим левую частьбалки. Q – поперечная сила - результирующая всех внутренних усилий алгебраически равна сумме всех сил, расположенных левее сечения. M – изгибающий моментрезультирующий момент всех внешних сил, численно равен алгебраической сумме моментов всех усилий, расположенных левее сечения. Составим уравнения равновесия для левой части: |
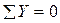 →
→ 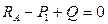 →
→ 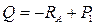
∑МсечХ=0; → 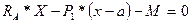 →
→ 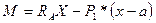 ;
;
Можно вместо левой части рассмотреть правую часть. Результат будет тот же, но с обратным знаком.
В связи с этим для того, чтобы в одном и том же сечении Q и M имели одинаковые знаки независимо от того какая часть рассматривается, примем следующее
ПРАВИЛО ЗНАКОВ(см. рисунок):
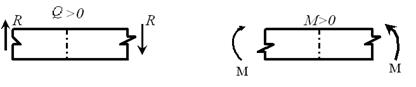
Поперечную силу будем считать положительной, если равнодействующая сила левее сечения направлена вверх, а правее сечения направлена вниз.
Изгибающий момент будет считаться положительным, если равнодействующий момент левых сил направлен по ходу часовой стрелки, а правых – против часовой стрелки.
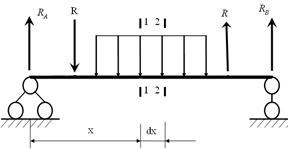
Зависимость между изгибающим моментом, поперечной силой и интенсивностью распределенной нагрузки.
|
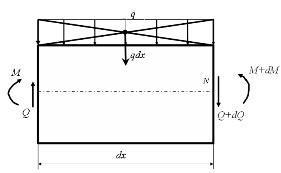
Выделим из балки участок бесконечно малой длины так чтобы по границам этого участка и по самом участке сосредоточенные силы отсутствовали.
Ввиду малости участка распределенную нагрузку 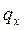 примем равномерно распределенной примем равномерно распределенной 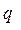 .
Составим уравнения равновесия: .
Составим уравнения равновесия: 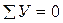 ; ;
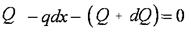
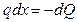 или или
|
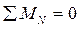 ;
; 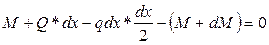 ;
; 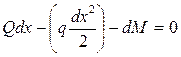
Пренебрегая бесконечно малыми величинами второго порядка, получаем: 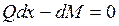 или
или
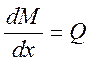
|
Продифференцировав последнее выражение по Х, получаем: 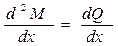 ; или
; или
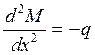
|
Построение эпюр изгибающих моментов и поперечных сил.
Внутренние усилия Q и M зависятот координаты Х, поэтому удобно иметь графики зависимости Q и M от расстояния Х, эти графики называются эпюрами поперечных сил и изгибающих моментов. Построение эпюр Q и M рассмотрим на частных примерах.
 Положительные изгибающие моменты будем откладывать в сторону растянутых волокон.
Положительные изгибающие моменты будем откладывать в сторону растянутых волокон.
| Пример 1.Построить эпюры Q и M.
1) Определяем опорные реакции: 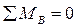 ; ;
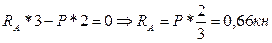 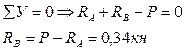 2) Разбиваем балку на участки.
Рассмотрим отдельные участки.
3) Участок 1: (рассекаем на расстоянии Х1)
2) Разбиваем балку на участки.
Рассмотрим отдельные участки.
3) Участок 1: (рассекаем на расстоянии Х1)
 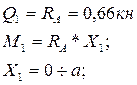
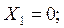 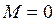
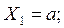 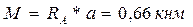 Участок 2: (рассекаем на расстоянии Х2)
Участок 2: (рассекаем на расстоянии Х2)
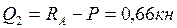
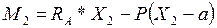
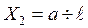
 при при 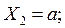 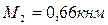 при
при 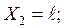 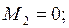 .
.
|
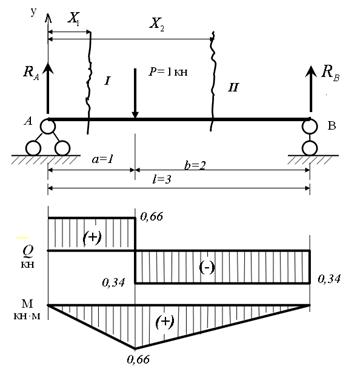
Пример 2.Построить эпюры Q и M.
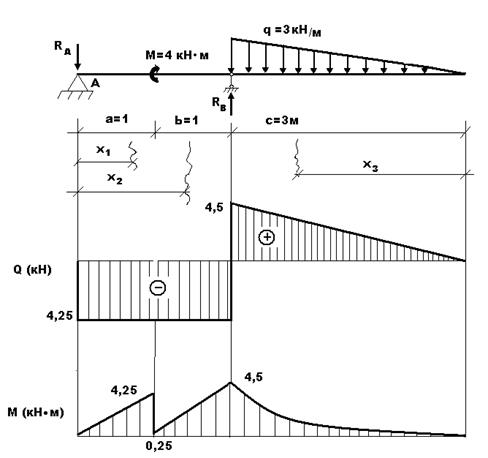
1) Определим опорные реакции:
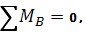
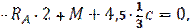
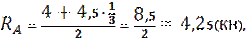
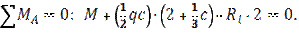
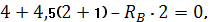
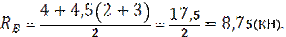
Проверка
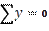
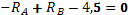 ,
,
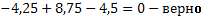
Следовательно, опорные реакции определены верно.
2) Построим эпюры Q и M:
Участок I: 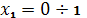
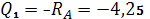
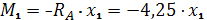
1) 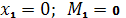
2) 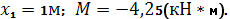
Участок II: 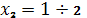
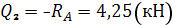
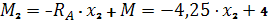
1) 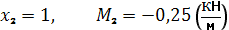
2) 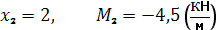
Участок III: 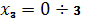
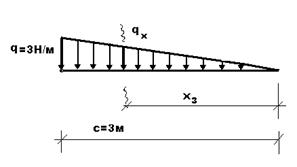
| Идем справа налево
Из подобия треугольников . находим:
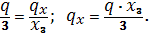
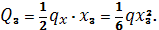
|
1) 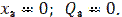
2) 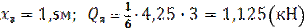
3) 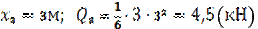
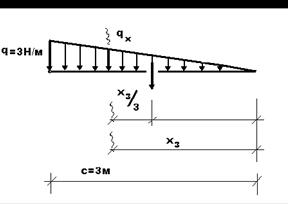
| 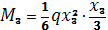 1)
1) 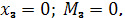 2)
2) 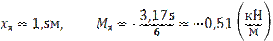 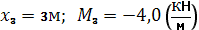
|
Контроль правильности построения эпюр Q и М
Дата добавления: 2016-02-13; просмотров: 1424;

