ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА

ЗАКОН ДИНАМИКИ ВРАЩАТЕЛЬНОГО

Вращательное движение точек твердого тела характеризуется угловым перемещением φ, угловой скоростью ω = dφ/dt и угловым ускорением β = dω/dt. При вращательном движении все точки тела имеют одинаковую угловую скорость и одинаковое угловое ускорение. Перемещение любой точки вращающегося тела за промежуток времени Δt можно измерить дугой окружности ΔS, пройденной точкой за это время. Выразим угловое перемещение точки тела Δφ в радианах и обозначим r - радиус окружности, описываемой данной точкой вокруг оси вращения, тогда

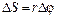
При очень малом угловом перемещении точки тела dφможно заменить малую дугу, пройденную точкой, прямолинейны отрезком dS, тогда

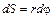
(1)

Это равенство устанавливает связь между линейным и угловым перемещением точек вращающегося тела. Линейная и угловая скорости, линейное и угловое ускорения точек вращающегося тела связаны между собой соотношениями:

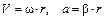
(2)

При поступательном движении перемещение, скорость и ускорение являются векторными величинами (полярные векторы). Во вращательном движении угловое перемещение, угловая скорость и угловое ускорение однозначно определяются лишь тогда, когда известно положение оси вращения в пространстве и указано направление поворота вокруг этой оси. Поэтому эти величины определяются тоже как векторы, направление которых связано с направлением вращения (аксиальные векторы).

Соотношение (2) в векторной форме имеет вид

(3)

Для определения направления вектора угловой скорости 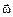удобно пользоваться правилом буравчика. Вектор угловой скорости направлен по оси вращения в сторону поступательного движения острия буравчика, когда рукоятку его вращают в направлении вращения тела. Направление вектора углового перемещения совпадает с направлением вектора угловой скорости. Если направление оси вращения остается неизменным, вектор углового ускорения 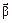при увеличении угловой скорости совпадает с ней по направлению, а при уменьшении - направлен в противоположную сторону. При изменении направления оси вращения тела вектор 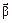не будет совпадать по направлению с вектором 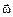. Поступательное движение твердого тела подчиняется второму закону Ньютона 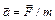, т.е. ускорение 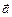зависит как от действия силы, так и от массы тела.

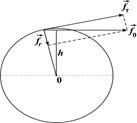
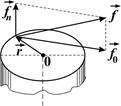
Рис. 1

Изменение скорости вращательного движения твердого тела, имеющего закрепленную ось вращения, обуславливается лежащей в плоскости, перпендикулярной к оси вращения, тангенциальной составляющей f_τсилы, действующей на тело (рис. 1). При этом угловое ускорение зависит не только от величины этой составляющей силы, но и от плеча. Плечом силы называют кратчайшее расстояние h от оси вращения до линии, вдоль которой действует сила. Поэтому в динамике вращательного движения вместо силы рассматривается момент силы относительно оси вращения.

Моментом силы 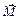относительно оси вращения называется вектор, модуль которого численно равен произведению силы на плечо . Направление вектора момента определяется по правилу буравчика. Если вместо плеча силы воспользоваться радиус-вектором точки приложения силы относительно оси вращения (рис. 1), то момент силы можно представить в виде векторного произведения:

(4)

Угловое ускорение вращающегося тела зависит не только от его массы, но и от распределения этой массы относительно оси вращения. Поэтому в динамике вращательного движения вместо массы рассматривают момент инерции тела относительно оси вращения.

Твердое тело можно представить как систему материальных точек. Скалярную величину , равную произведению массы материальной точки на квадрат расстояния её от оси вращения, называют моментом инерции материальной точки относительно данной оси. Сумму моментов инерции всех точек тела относительно оси вращения называют моментом инерции относительно оси:

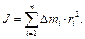
(5)

Зависимость углового ускорения тела от момента действующей на тело силы и момента инерции тела относительно неподвижной оси, вокруг которой происходит вращение, определяется основным законом динамики вращательного движения:

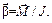
(6)