ЗАДАЧА 10. ГАЗОВЫЙ ЛАЗЕР, НАБЛЮДЕНИЕ НЕКОТОРЫХ ЯВЛЕНИЙ ИНТЕРФЕРЕНЦИИ И ДИФРАКЦИИ В ВЫСОКОКОГЕРЕНТНОМ ИЗЛУЧЕНИИ

Для источников света, традиционных в оптической области спек­тра, характерна некогерентность излучения. Поэтому для наблюдения явлений интерференции необходимо применять специ­альные методы получения когерентных пучков. Из-за немонохроматичности света не удается наблюдать интерференцию и дифракцию при боль­ших разностях хода, так как в этом случае интервал используемых длин волн Dl надо брать очень узким. Например, нельзя наблюдать ин­терференцию в толстых пластинках.

В начале 60-х годов были созданы источники света иного типа, получившие название оптических квантовых генераторов (ОКГ) или ла­зеров. В противоположность некогерентным источникам, электромагнит­ные волны, зарождающиеся в различных частях лазера, удаленных друг от друга на макроскопические расстояния, оказываются когерентными между собой. Кроме когерентности, лазерное излучение обладает ещё такими важными свойствами, как высокая степень монохроматичности и острая угловая направленность (коллимация) светового пучка.

Когерентность излучения проявляется практически во всех свой­ствах ОКГ. Замечательной чертой лазеров, тесно связанной с когерен­тностью их излучения, является способность к концентрации энергии – во времени, в спектре, в пространстве, по направлени­ям распространения. Для некоторых характерна чрезвычайно высокая степень монохроматичности излучения. Другие лазеры испускают очень короткие импульсы, продолжительностью 10^-12 с, поэтому мгновенная мощность такого излучения бывает очень высокой. Лазерный световой пучок обладает высокой степенью направленности. Это позволяет сфо­кусировать его на ничтожно малой площади и создать огромную осве­щенность.

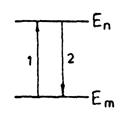Рассмотрим физические процессы, лежащие в основе работы ОКГ. Одним из необходимых условий возникновения лазерного излучения является создание так называемой инверсной заселенности уровней рабочего вещества лазера. Чтобы понять, что это значит, рассмотрим, для простоты, совокупность атомов, которые могут находиться в двух энергетических состояниях, характеризуемых энергиями E_m и E_n (рис.1). Число атомов N_m и N_n, находящихся в состоянии с заданной энергией, называется заселенностью данного уровня. Заселенности зависят от условий, внеш­них по отношению к атому. В состоянии термодинамического равновесия при температуре Т заселенности определяются принципом Больцмана

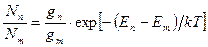
Здесь g_m и g_n – так называемый статистиче­ский вес, представляющий собой число различных квантовых состояний в данном интервале значений энергии.

В неравновесных условиях заселенность уровней определяется временем t_n нахождения атома в данном состоянии и вероятностью W_mn перехода из одного состояния в другое N_n = W_mn×t_n.

Пусть в нашем случае состояние атома с энергией E_m является невозбужденным, а с энергией E_n – возбужденным. Если атом поглотит определенную порцию энергии, то он может перейти в возбужденное состояние E_n (переход 1). При отсутствии внешних воздействий атом возвращается в исходное сотояние с меньшей энергией, испуская при этом квант света величины hn=E_n – E_m. Такой процесс называется самопроизвольным, или спонтанным, испусканием света, а соответствую­щие переходы – спонтанными (переход 2).

Оказывается, кроме спонтанного, может существовать индуцированное (вынужденное, или стимулированное) излучение. Оно состоит в радиации фотона под действием внешнего электромагнитного поля, т.е. переход типа 2 будет происходить не самопроизвольно, а под действи­ем внешних причин. Таким образом, в общем случае следует считать, что наблюдаемое излучение представляет собой сумму энергий спонтанных и индуцированных излучательных переходов. Энергии этих переходов определяются заселенностью возбужденного уровня.

Для обычных источников света большинство атомов находится в невозбужденном состоянии, т.е. N_m >> N_n, и в них, как правило, происхо­дят спонтанные переходы.

Для создания вынужденного излучения необходимо, чтобы вероят­ность спонтанных переходов E_n ® E_m была близкой к нулю. Существуют вещества, у которых атом мо­жет находиться в возбужденном состоянии достаточно долго. Энергетические уровни, соответству­ющие этим состояниям, называются метастабильными. Если мы теперь ка­ким-то путем будем переводить атомы из основного состояния в воз­бужденное, число атомов в возбужденном состояний n будет расти, а число атомов в состоянии m – уменьшаться. В конце концов, можно до­стичь такой ситуации, когда N_n > N_m.

Этот случай носит название ин­версной заселенности возбужденных уровней. Если теперь внешним элек­тромагнитным полем осуществить переход E_n ® E_m одновременно для всех атомов, то получим вынужденное излучение большой мощности, при­чем оно будет когерентным, т.к. все атомы переведены в основное со­стояние одной и той же вынуждающей силой.

В условиях термодинамического равновесия свет, проходя через вещество, поглощается по закону Бугера. При этом коэффициент поглоще­ния a(n) > 0. Однако при инверсной заселенности возбужденного уровня a становится отрицательным. В этом случае плотность потока энергии, распространяющейся в среде, будет возрастать, так как за счет индуцированного излучения в световой пучок будет добавляться больше фотонов, чем он теряет на возбуждение атомов при обратных переходах (m®n).

Среду с инверсной заселенностью энергетических уровней, обеспечивающую усиление распространяющегося излучения, называют активной. Возможность осуществления инверсной заселенности возбужденного со­стояния и позволила создать ОКГ.

Однако, наличие активной среды ещё не достаточно для возникнове­ния лазерного излучения. Чтобы его создать, эту среду помещают меж­ду двумя зеркалами типа используемых в интерферометрах Фабри-Перо (рис.2). Такая система называется активным оптическим резонатором.

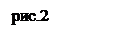
Пусть возбужденный атом, расположенный в точке A, испускает волну в результате спонтанного перехода между уровнями с инверсной заселенностью. Чем больше путь, проходимый волной в активной среде, тем больше её усиление. Для направлений, перпендикулярных к оси резонатора, усиление оказывается наименьшим. При распространении волны вдоль оси она пройдет больший путь, усилится значительнее, затем от­разится от зеркала, вновь пройдет через активную среду, усиливаясь при этом, достигнет противоположного зеркала, отразится и т.д.

Помимо усиления активной средой, существуют ряд факторов, кото­рые уменьшают амплитуду волны внутри резонатора. Это связано с тем, что коэффициент отражения зеркал меньше единицы, кроме того, для вы­вода излучения из резонатора одно из зеркал делается частично про­зрачным. При распространении излучения вдоль оси резонатора будут возникать и другие потери, вызванные дифракцией излучения, рассеяни­ем его в самой среде и т.п. Усиление волны будет происходить до тех пор, пока не установится стационарный уровень.

*В качестве активной среды ОКГ ис­пользуются твердые тела, жидкости и га­зы. Лазеры на твердых телах работают, как правило, только в импульсном режиме. Жидкостные и газовые могут работать и в непрерывном режиме.

Создание инверсной заселенности уровней (иначе говоря "накачка") осуществляется различными способами. Твер­дотельные и жидкостные лазеры "накачи­ваются оптическим путем, газовые - с помощью электрического поля.

В данной работе используется гелий-неоновый лазер непрерывно­го действия.

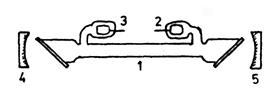Принципиальнаясхема его устройства показана на рис.3. Здесь 1 – газоразрядная стеклянная трубка диамет­ром несколько мм и длиной от десятков см до 1,5 м и более. Торцы трубки закле­ены плоскопараллельными стеклянными или кварцевыми пластинками, ориентированными под углом Брюстера к оси трубки. Для излучения, распространяющегося вдоль оси трубки и поляризованного в плоскости падения света на плас­тинки, коэффициент отражения от них равен 0. Давление гелия в труб­ке порядка 1 мм рт.ст., неона – 0,1 мм рт.ст. Трубка имеет катод 2 и цилиндрический пустотелый анод 3, между которыми накладывается напряжение 1 – 2,5 кВ. Разрядная трубка помещается между зеркалами 4 и 5. Зеркала, обычно сферические, делаются с многослойными диэлек­трическими покрытиями, имеющими высокие значения коэффициента отра­жения и почти не обладающими поглощением света. Пропускание одного зеркала – около 2%, другого – менее 1%. Если лазер включить, то при правильной ориентации через оба зеркала распространяются хорошо коллимированные интенсивные пучки монохроматического (красного) света с длиной волны 632,8 нм. Ответственными за это излучение яв­ляются атомы неона. Гелий-неоновый лазер может генерировать и линию l = 1150 нм, но для её получения торцевые окна газоразрядной труб­ки и зеркала резонатора надо подбирать для инфракрасной области спектра.

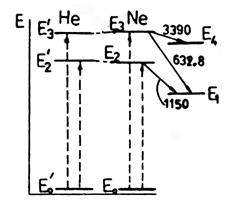Рассмотрим процессы, которые обеспечивают инверсную заселен­ность уровней неона. На рис.4 приведена схема уровней He и Ne, кото­рые обусловливают возникновение лазерного излучения. Другие уровни не показаны.

Излучению с l = 632,8 и 1150 нм соответствуют переходы E₃ ® E₁ и E₂ ® E₁. Атомы неона возбуждаются газовым разрядом и при определен­ных режимах работы этот процесс оказывается достаточным для обра­зования инверсной заселенности уровней E₁ и E₂. Но уровни E₃, E₁ и E₃, E₄, переходы между которыми отвечают l = 632,8 и l = 3390 нм,заселены не инверсно. Положение меняется, если в разрядную трубку ввести гелий. He обладает двумя метастабильными состояниями E₃' и E₂'. Эти состояния возбуждаются при столкновении с электронами. Ввиду большой длительности их суще­ствования концентрация метастабильных атомов гелия в разряде очень велика. Энергии E₃' и E₂' очень близки к E₃ и E₂ неона, что благоприятно для передачи энергии возбуждения от гелия к неону при их стол­кновениях (пунктирные горизонтальные стрелки). В результате концентрация атомов Ne, находящихся на уровнях E₃, E₂ резко увеличивается и возникает инверсная заселенность уровней E₂, E₁, а разность заселенностей уровней E₂, E₁ увеличивается в несколько раз.

В данной работе гелий-неоновый лазер используется в качестве высококогерентного источника излучения для наблюдения некоторых явлений интерференции и дифракции.

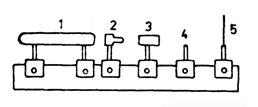Описание установки. Установка (рис.5) состоит из оптической скамьи, на которой установлены лазер 1, микрообъектив 2, столик 3 для расположения на нем различных приспособлений, рейтер 4 для за­крепления в нем в специальном держателе стеклянной пластинки и экран 5.

Упражнение 1. Определение длины волны излучения лазера с помощью дифракционной решетки. Направленность и пространственная когерентность излучения ла­зера позволяет применять ла­зерный световой пучок в ря­де измерений без предвари­тельной его коллимации. Ис­пользуем это свойство лазер­ного луча в опытах с дифрак­ционной решеткой. Для этого в установке убирают микрообъектив 2, на столик 3 ставят дифракционную решетку перпендикуляр­но световому лучу. Выполняют это таким образом. Поворачивая столик с решеткой, приводят световой блик, отраженный назад к лазеру от плоскости решетки, точно на середину выходного окна лазера.

После этого переходят к наблюдению и измерениям дифракционной картины на экране. Поскольку излучение лазера монохроматично, то на экране спектр будет представлять собой набор красных точек положи­тельных и отрицательных порядков, повторяющих сечение первичного пучка света. Установив экран перпендикулярно оси светового пучка, замеряют расстояние между нулевым и последующими максимумами раз­ных порядков. Измерения заключаются в многократных определениях расстояний Dx_m между дифракционными максимумами, соответственно, ±1-го, ±2-го, ±3-го и т.д. порядков, вплоть до наиболее далеких, укладывающихся на экране.

Очевидно, , где L – расстояние от плоскости дифракци­онной решетки до плоскости экрана, j_m – угол дифракции m-го поряд­ка. Пользуясь соотношением 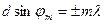, где d – период решетки, находят значение l из каждого измерения. Вычислит среднее значе­ние A и определяют погрешность измерений.

Упражнение 2. Наблюдение дифракции света на одной и двух щелях. Вместо дифракционной решетки устанавливают пластинку, на которой имеются одна и две, близко расположенные, узкие щели. Перемещают столик и вводят луч в одну щель. В этом случае на экране видна характерная дифракционная картина от одной щели. В центре нее выделяется своей интенсивностью широкий дифракционный максимум нулевого по­рядка. Максимумы более высоких порядков менее интенсивны. После этого вводят в луч две щели. При такой последовательно­сти действий становится сразу очевидным, что нового вносит в картину на экране интерференционный эффект двух световых пучков. Об­ласть расположения на экране дифракционных максимумов всех поряд­ков теперь изрезывается целой системой светлых и темных интерфе­ренционных полос. Эффект особенно заметен на ярком дифракционном максимуме нулевого порядка. Эта система интерференционных полос представляет собой искомое явление. Наблюдаемый эффект служит убе­дительным доказательством пространственной когерентности лазерно­го излучения.

В данном упражнении необходимо определить ширину щелей и рассто­яние между ними. Ширина отдельной щели может быть найдена из условий, связывающих углы фраунгоферовой дифракции на щели с её ши­риной. Для дифракционного минимума в этом случае , где т = ±1, ±2 и т.д., b – ширина щели, j_m – углы дифракции. Углы дифракции, соответствующие максимумам интенсивности, начиная с ±1 порядка, определяются из условий:

; ;

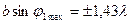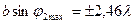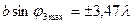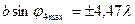; , и т.д.

Измерив на экране линейные удвоенные симметричные смещения Dx_i минимумов и максимумов света от середины максимума нулевого порядка, находят 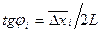( 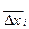– среднее значение) так, как это делалось в упражнении 1, и подставляя sinj_i в приведенные выше формулы, находят значение ширины щели b.

Определение расстояния d между двумя близкими щелями делают по интерференционной картине, расположенной в пределах дифракцион­ного максимума нулевого порядка. В этом случае для темных полос вы­полняется условие 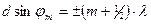. Ввиду расположения наблюдае­мых интерференционных полос в пределах лишь дифракционного макси­мума нулевого порядка можно положить sinj = j. Тогда, если 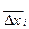– сред­нее расстояние между темными интерференционными полосами на экра­не, можно записать 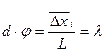или 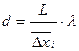. Найдя 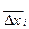и L, вычисляют расстояние между щелями d.

Упражнение 3. Фраунгоферова дифракция на малых круглых частицах. Чтобы углы дифракции на мелких частицах были значительны, раз­мер частиц должен быть малым. Но дифракционная картина от одной та­кой частицы будет очень слаба. Для наблюдения ярко выраженного эф­фекта можно поместить на пути светового луча множество хаотично расположенных одинаковых частиц. В данном случае в качестве таких частиц используется ликоподий (споры растения плауна), который по­мещается между двумя прижатыми друг к другу стеклянными пластинами. Ликоподий устанавливают на столике вместо дифракционной решетки. Проходя через частицы, лазерный луч на экране образует систему кон­центрических темных и светлых дифракционных колец, окружающих свет­лый круг. Поскольку в установке после стеклян­ных пластин с частицами ликоподия, вызвавшими дифракцию света, не установлен объектив и используется непосредственно уда­ленный экран, дифракционные кольца получаются широкими. Угловые радиусы тёмных колец подчиняются условиям:

; ; ,

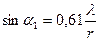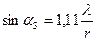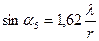где r – радиус частиц.

Для угловых размеров светлых колец

; ;

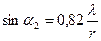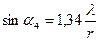Нумерация колец начата с первого темного кольца, окружающего центральный светлый круг.

Для определения радиуса частиц находят из опыта значения углов a. Очевидно, что 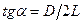, где D – линейный размер соответству­ющего дифракционного кольца на экране, L – расстояние от стеклян­ных пластин с ликоподием до экрана. Таким образом, измерив D и L, находят r.

Упражнение 4. Интерференция при больших разностях хода. Высокая степень монохроматичности излучения лазера позволяет осуществить наблюдение интерференционных полос равного наклона при большой разности хода и определить соответствующие им порядки ин­терференции.

Для наблюдения интерференционных полос равного наклона используется световой пучок с большой угловой апертурой, освещающий плоскопараллельный слой прозрачного вещества. Схема опыта показана на рис.6. Микрообъектив I собирает па­раллельный световой пучок лазера в фокусе F. Расходящийся из F световой конус достигает плоскопараллельного диска 3. Отраженные от перед­ней и задней поверхностей диска свето­вые волны дают интерференционную кар­тину в виде концентрических колец на экране 2. Интерференционное условие максимума отраженного света для угла падения i запишется:

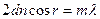(1)

где d – толщина пластинки, n – её показатель преломления, m – искомый порядок интерференции. Угол падения света - связан с уг­лом его преломления в пластинке r соотношением sini/sinr = n. При малости этих углов можно записать i/r = п. На опыте можно изме­рить радиусы R_m = FA нескольких интерференционных колец и рассто­яние L = FО. Тогда

(2)

Зная т, можно найти r_m. После этого, применив формулу (1) к нескольким измерениям, можно, исключив d, вычислить m_max, т.е. максимальный порядок интерференции в условиях опыта.

Измерения выполняются следующим образом. Помещают в установке (рис.6) микрообъектив с надетым на него экраном 2 и центрируют его на пути луча. На некотором расстоянии L ставят стеклянный диск перпендикулярно лучу. Включают лазер и путем юстировки диска доби­ваются того, чтобы наблюдающиеся на экране интерференционные кольца располагались концентрически относительно микрообъектива. Затем из­меряют радиусы темных интерференционных колец R и расстояние L.

Перед измерениями следует, прежде всего, перенумеровать (K_x = 0, 1, 2, 3, ...) интерференционные полосы. Нулевой номер приписывается, например, первому видимому на экране темному кольцу вблизи отверстия в экране. Следующие номера идут в возрастающей по­следовательности. Правильная нумерация колец имеет решающее значе­ние при последующей обработке результатов.

На опыте измеряются не радиусы, а диаметры колец с помощью перпендикулярных лекал, нанесенных на поверхность экрана. Из средне­го значения длин двух диаметров находят среднее значение радиусов темных интерференционных колец R_k. Зная R_k и L, по формуле (2) наводят значения углов i для всех промеренных полос.

Дальше результаты измерений обрабатывают следующим образом. Исходя из малости i и r,можно записать

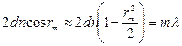
Отсюда, с учетом, что m_max = 2dn/l получим

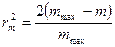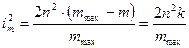или , (3)

где K = m_max – m. Величина 2dn/l не обязательно будет целым числом. Другими словами, в центре интерференционной картины, где r = 0, не обязательно будет темное пятно. Однако при больших значениях m в условиях задачи можно пренебречь его дробной долей.

Из (3) видно, что 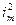является линейной функцией K. Однако истин­ного значения K мы не знаем. Поэтому поступаем следующим образом. Припишем номер 0 произвольному видимому на экране кольцу. Пусть номера последующих колец в порядке увеличения их радиусов – K_X. Тогда для любого кольца с условным номером K_X истинное значение K = K₀ + K_X,где K₀ – число неучтенных темных интерференционных полос между центром интерференционной картины и условным нулевым кольцом. С учетом этого выражение (3) перепишется так:

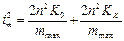(4)

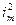оказывается линейной функцией K_{X .} График 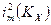будет выглядеть, как показано на рис. 7. Как видно из графика, путем экстраполяции можно из него найти K₀. Из графика также ясно, что тангенс угла наклона этой зависимости дает возможность найти m_max:

.

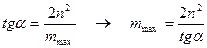Таким образом, по экспериментальным данным строим зависимость 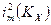. По ней определяем K₀ и m_max. Зная K₀, оцениваем истинные значения порядков интерференции m = m_max ×K₀ – K_X всех промеренных интерференционных колец. При вычисления использовать n = 1,5.

Литература: 1, 2.