ЗАДАЧА 9. ОПРЕДЕЛЕНИЕ ВЫСОКИХ ТЕМПЕРАТУР С ПОМОЩЬЮ ОПТИЧЕСКОГО ПИРОМЕТРА

Измерение высоких температур с достаточной степенью точности – это важная проблема, с которой довольно часто приходится сталкивать­ся в современной науке и технике. Решение её невозможно с помощью обычных прямых методов измерения температуры. Действительно, все эти методы основаны на том, что какое-либо тело с хорошо изучен­ными физическими свойствами приводится в непосредственный контакт с нагретым веществом, и о температуре вещества судят по изменению состояния указанного тела, например, по изменению объема жидкости в термометре. Однако, при высоких и сверхвысоких температурах не толь­ко существенно меняются физические свойства всех известных нам тел, но происходят качественные изменения (химические) этих тел, и выбор материалов, пригодных для прямого измерения, становится невозможным. Кроме того, не каждый исследуемый высокотемпературный объект доступен для непосредственного измерения температуры. К таким объектам относятся космические тела.

Следовательно, прямые методы измерения в случае высоких темпе­ратур приходится заменять косвенными, позволяющими определять сте­пень нагретости тела, не вступая в непосредственный контакт с ним. Основой этих косвенных методов является возможность исследования на расстоянии излучения, испускаемого нагретым телом.

Тепловым излучением называется непрерывный спектр электромаг­нитной энергии, который всякое нагретое тело излучает в окружающее пространство.

Совокупность методов измерения температуры, основанных на ис­следовании свойств теплового излучения, носит название оптической пирометрии.

Рассмотрим основные законы теплового излучения. Выберем в каче­стве характеристики теплового излучения величину энергии Ф, т.е. ко­личество энергии, излучаемой телом в единицу времени. Наблюдения по­казали, что тела, хорошо излучающие энергию, одновременно хорошо по­глощают её. Кроме того, было установлено, что количество излучаемой и поглощаемой телом энергии существенно зависит от двух параметров: температуры тела и длины (частоты) излучаемых или поглощаемых электромагнитных волн.

Таким образом, поток энергии является функцией температуры Т и частоты излучения n и поэтому будем в дальнейшем обозначать его через Ф_n,Т.

Назовем излучательной способностью тела e_n,Т отношение светово­го потока, излучаемого единицей поверхности тела при данной темпе­ратуре в спектральном интервале от n до n + dn, к ширине этого спектрального интервала

(1)

Введем также понятие поглощательной способности тела A_n,Т, оп­ределив её как отношение поглощаемого единицей поверхности тела светового потока dФ'_n,Т падающему потоку dФ_n,Т при температуре Т и частоте n

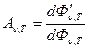(2)

Величина A_n,Т, по определению, представляет собой правильную дробь, которая может принимать, в зависимости от природы тел, все значения от нуля до единицы. Минимальное значение A_n,Т (нуль) имеет тело, полностью отражающее весь падающий на него поток энергии (абсо­лютно отражающее тело). Максимальным значением A_n,Т (единица) обла­дает тело, которое полностью поглощает всю падающую на него лучис­тую энергию (абсолютно черное тело). В действительности в природе не существует ни абсолютно черных, ни абсолютно отражающих тел, они представляют собой некоторую физическую идеализацию. Однако, как будет видно из дальнейшего, понятие об абсолютно черном теле имеет большое теоретическое значение и играет в теории теплового излуче­ния важнейшую роль. Эту роль оно приобрело с момента открытия Кирх­гофом в 1859 году основного закона теплового излучения.

Закон Кирхгофа гласит: отношение излучательной способности к поглощательной не зависит от природы тела и представляет собой универсальную для всех тел функцию частоты излучения и температу­ры.

Если излучательные способности физических тел обозначить через e⁽¹⁾_n,Т, e⁽²⁾_n,Т, e⁽³⁾_n,Т, …, а поглощательные соответственно через A⁽¹⁾_n,Т, A⁽²⁾_n,Т, A⁽³⁾_n,Т, …, то закон Кирхгофа можно выразить следующим матема­тическим выражением

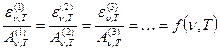, (3)

где f(n, T) – некоторая функция частоты излучения и температуры. Пусть среди рассматриваемых тел имеется абсолютно черное. Тогда знамена­тель одной из дробей в выражении (3) обращается в единицу, и это выражение может быть переписано таким образом:

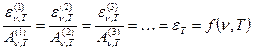, (3)

где e_T – излучательная способность абсолютно черного тела. Из вы­ражения (4) становится ясным физический смысл функции f(n, T) и закон Кирхгофа может быть сформулирован в следующем виде: излучательные и поглощательные способности могут быть различными для разных тел, однако отношения их являются постоянными для всех тел и равны излучательной способности абсолютно черного тела.

Хотя абсолютно черных тел не существует, наиболее близкими к ним по своим свойствам являются сажа и платиновая чернь. Можно также построить искусственное черное тело, взяв, например, сферическую по­лость, окрашенную изнутри в черный цвет, и проделав в ней очень ме­ленькое отверстие, диаметр которого не превышает 0,1 диаметра полости. Свет, падающий в полость сферы через отверстие, при падении на стенку будет частично поглощаться ею, и частично отражаться. Благодаря многократным отражениям луча света и малости отверстия лучистая энергия практически вся будет оставаться в полости сферы, т.е. в конце световые лучи окажутся полностью поглощенными.

Из закона Кирхгофа следует, что излучательная способность абсо­лютно черного тела является наивысшей. Излучательная способность любого другого тела всегда меньше. Очевидно также, что для того, что­бы характеризовать тепловое излучение любого тела, необходимо знать явный вид зависимости от частоты излучения и температуры излучательной способности абсолютно черного тела. Эта общая задача была решена только через сорок с лишним лет после того, как она была поставлена Кирхгофом. Однако в ходе её решения удалось установить ряд частных закономерностей, которым подчиняется излучение абсо­лютно черного тела.

Стефан экспериментально в 1879 году и Больцман теоретически на основе термодинамики в 1884 году установили, что суммарная энергия всего спектра электромагнитных волн, излучаемых о единицы поверхности абсолютно черного тела в единицу времени, пропорциональна четвертой степени его абсолютной температуры:

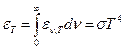, (5)

где s = 5,71×10^-12 Вт/см²град⁴.

Вин в 1983 году, также пользуясь термодинамическими методами, теоретически решил вопрос о распределении энергии в спектре излу­чения абсолютно черного тела. Он установил, что длина волны l_max, на которую приходится максимум излучательной способности, закономерно меняет­ся от абсолютной температуры тела, а имен­но, с повышением температуры абсолютно черного тела максимум его излучательной способности смещается в сторону более коротких длин волн (более высоких час­тот) (рис.1). Это – закон смещения Вина. Математически закон Вина записывается следующим образом

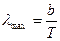, где b = 2886 микрон×град. (6)

Расчет показывает, что при практически достижимых Т максимум излучательной спо­собности абсолютно черного тела лежит в инфракрасной области спектра: при Т = 3000К l_max = 920 нм. Лишь при Т = 5000К l_max = 577 нм. Вином установ­лен ещё один закон излучения, гласящий, что максимальная излучательная способность e_lmax абсолютно черного тела возрастает пропорционально пятой степени абсолютной температуры:

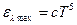(7)

Основные закономерности теплового излучения абсолютно черного тела, указанные выше, были получены на основе классической термодинамики. Однако явный вид зависимости e(n, T), отвечающий эксперимен­ту, удалось найти только исходя из квантовых представлений о приро­де электромагнитного излучения. В 1900 году Планк вывел общую фор­мулу, согласно которой

(8)

Можно показать, что все установленные ранее термодинамические законы излучения абсолютно черного тела легко выводятся из форму­лы Планка.

Метод измерение яркостной температуры. Приборы, служащие для измерения температуры, в основе работы ко­торых лежат законы теплового излучения, называются оптическими пирометрами. Наиболее распространенный способ оптического определения температуры основывается на сравнении излучения нагретого тела в одном определенном спектральном участке l с излучением черного тела той же длины волны. Сравнение это с наибольшим удобством осу­ществляется при помощи пирометра с исчезающей нитью, схема принци­пиального устройства которого показана на рис.2. В фокусе объектива О помещается электрическая лампа L с нитью, пря­мой либо изогнутой в форме дуги. Окуляр Ок позволяет на­блюдать одновременно сред­нюю часть нити и изображе­ние поверхности исследуемо­го источника, проектируемого при помощи объектива О в плоскость нити. Красное стекло F, помещенное между окуляром и глазом, пропускает свет в области l = 660 нм. Лампа питается током от батареи B, который регулируется реостатом R. Ток питания определяется с помощью амперметра А. (Обычно амперметр А и реостат монтируются в корпусе пирометра, причем R изготовля­ется в виде кольца.) При измерении температуры регулируют ток в ни­ти до тех пор, пока последняя не исчезает на фоне изображения ис­следуемого источника. При этом яркости излучения нити и исследуемо­го источника для l = 660 нм совпадают и, следовательно, для данной l совпадают и их излучательные способности. Амперметр пирометра предварительно градуируют по температуре при помощи наблюдения черного тела, нагретого до различных значений Т. Таким образом, по показаниям амперметра мы можем судить, какой температуре черного тела Т соответствует излучение наблюдаемого источника. Если бы ис­точник был также черным телом, то найденная Т была бы его истинной температурой. В противном случае найденная температура характеризу­ет температуру Т черного тела, имеющего для l = 660 нм ту же яркость, что и излучающее тело при условиях наблюдения. Поэтому Т носит наз­вание яркостной температуры исследуемого источника. (Будем обозна­чать яркостную температуру через Т_Я, а истинную, – или термодинами­ческую, – через Т_И) Если изучаемое тело не абсолютно черное, то всегда Т_Я < Т_И. Это связано с тем, что любое тело излучает меньше, чем абсолютно черное при той же температуре. Следовательно, произвольное тело, имеющее в данный момент одинаковую яркость (для определенной l) с некоторым черным телом, имеет наверняка термодинамическую температуру выше температуры черного тела, т.е. выше той яркостной температуры, которая определяется с помощью нити пирометра, прокали­брованной по излучению абсолютно черного тела.

Различие между Т_И и Т_Я может быть значительным. Например, для вольфрама вблизи температуры 1000°C яркостная температура на 44° ниже термодинамической, а при 3000°C – уже на 327°. Связь между Т_Я и Т_И для данного тела устанавливается соотношением

(9)

Величина e_l,Т индивидуальна для каждого материала.

С₁ = hc/k = 1.438 см×град., где h - постоянная Планка, с – скорость света, k – постоянная Больцмана. Учитывая, что значение Т_Я близко к значению Т_И, формулу (9) можно переписать так

, (10)

где DТ означает всегда положительную поправку к измеренной с по­мощью пирометра яркостной температуре Т_Я. Тогда

Т_И = Т_Я + DТ (11)

В данной работе используется пирометр, измерительный прибор которого содержит две шкалы температур - верхнюю и нижнюю. Верхняя шкала позволяет проводить измерения в пределах от 880°С до 1400°С, нижняя - в пределах 1200 ¸ 2000°С. Температуру нити пирометра нель­зя повышать выше 1400°С. Чтобы уравнять яркости свечения нити пиро­метрической лампы и исследуемого тела при Т > 1400°С, между нитью и объективом вводится специальный фильтр, ослабляющий излучение тела в определенное число раз. В этом случае после выравнивания яркостей отсчет температуры проводится по верхней шкале. Фильтр вводится с помощью специальной головки, расположенной сверху на тубусе, в ко­тором закреплен объектив пирометра.

В работе ставится задача научиться пользоваться оптическим пирометром, определить температуру исследуемого источника при различных потребляемых мощностях, а также проверить закон смещения Вина.

Источником излучения служит лампа накаливания с вольфрамовой лентой. (Для вольфрама e_l,Т = 0,45 при l » 660 нм). Лампа питается через ЛАТР. В её цепь включены амперметр и вольтметр для определе­ния потребляемой мощности. Установка содержит также монохроматор с приемником излучения и гальванометром, которые служат для проверки закона смещения Вина. В качестве приемника излучения исполь­зуется кремниевый фотодиод.

Измерения выполняются в следующем порядке.

1. Готовят пирометр к измерениям. Для этого поворачивают коль­цо реостата влево до отказа и замыкают цепь накала нити. Наблюдая в окуляр, плавным вращением реостата доводят нить до красного ка­ления и продольным перемещением тубуса окуляра добиваются отчет­ливого изображения нити в поле зрения.

2. Включают исследуемую лампу, подают на неё напряжение 3 ¸ 4 вольта. Наводят на неё пирометр и путем продольного перемещения тубуса объектива добиваются её четкого изображения в поле зрения.

3. Меняя напряжение на лампе в интервале 1,5 ¸ 5,5 В через 0,5 В, при каждом значении потребляемой мощности определяют яркос­тную температуру источника. (Для нахождения мощности одновременно измеряют ток в цепи лампы.)

4. Выключают цепь питания пирометра, предварительно повернув кольцевой реостат влево до отказа. Лампу устанавливают так, чтобы её излучение попадало через линзу на входную щель монохроматора и измеряют спектры излучения при двух значениях напряжения на лампе V₁ = 2 В и V₂ = 5,5 В. После этого выключает всю измерительную установку.

Обработку результатов измерений проводят следующим образом.

1. Приводят полученные значения яркостной температуры к абсо­лютной шкале температур.

2. Пользуясь формулами (10) и (11), находят истинные темпера­туры нити лампы. Для расчётов принимают l = 660 нм, e_l,Т = 0,45.

3. Вычисляют с точностью до 0,1 Вт мощность, подводимую к нити исследуемой лампы, для каждого значения термодинамической температуры, и строят график зависимости расходуемой в лампе мощности от Т_И ее нити.

4. Строят спектры излучения, полученные для двух разных темпе­ратур, и определяют их взаимное смещение.

5. Известно, что для черного тела полная энергия излучения

(12)

Для нечерного тела значение Е определяется выражением

(13)

При этом величины B и n оказываются различными для различных температурных интервалов. Но ВТⁿ всегда меньше sT⁴. Проведенные измерения позволяют найти n в изученном интервале температур следующим образом. При высокой температуре подводимая к исследуемой спирали лампы мощность W почти полностью расходуется на излучение, т.е.

.

Отсюда

(14)

Построив эту зависимость в координатах lgТ_И – lgW, найдемn, как тангенс угла наклона полученного графика к оси абсцисс.

Литература: 1, 2, 3.