Поступательное движение механической системы

В этом случае все точки системы движутся с одинаковыми скоростями (свойства поступательного движения тела). Поэтому, выражение (14.75) можно преобразовать, вынеся за знак суммы постоянные величины:

или:

где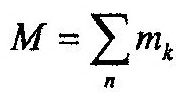

– масса механической системы.

Таким образом, кинетическая энергия механической системы при ее поступательном

Движении равна половине произведения массы системы на квадрат ее скорости.

Вращательное движение механической системы

Рассмотрим тело (рис. 14.14), совершающее вращательное движение относительно вертикальной оси z. Представим это тело как механическую систему точек. Найдем для него формулу кинетической энергии, используя выражение (14.75), получим:

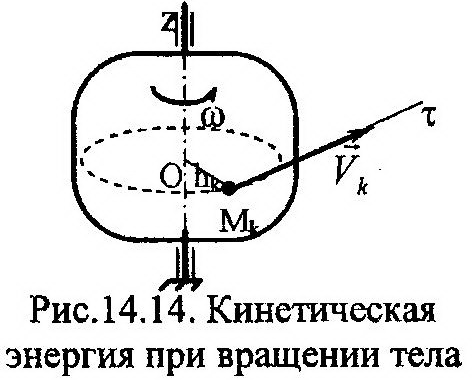
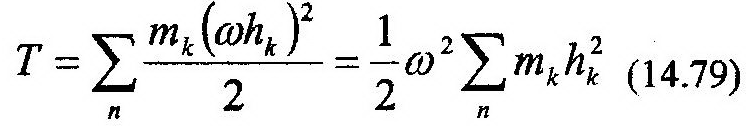или:

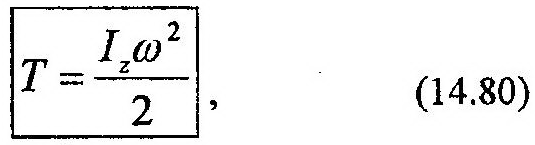
где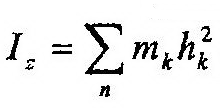

– момент инерции тела относительно оси z.

Кинетическая энергия механической системы при ее вращательном движении равна половине произведения ее момента инерции, взятого относительно оси вращения, на квадрат угловой скорости.

Сравнивая формулы (14.78) и (14.80), нетрудно заметить, что между ними имеет место прямая аналогия. Действительно, в обоих случаях величина кинетической энергии определяется как половина произведения меры инертности тела (масса или момент инерции) на квадрат ее скорости.