Работа внутренних сил твердого тела
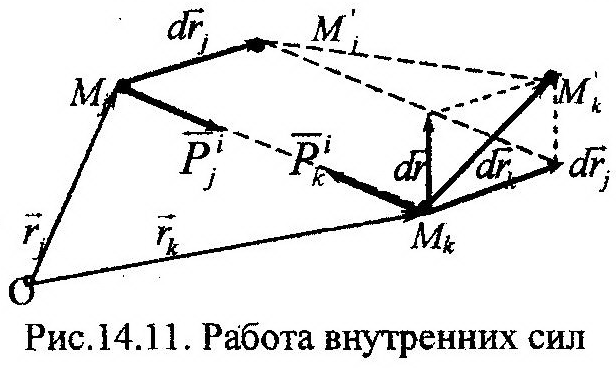
Представим твердое тело как совокупность материальных точек, определенным образом связанных друг с другом. Зададим телу элементарное перемещение в пространстве. При этом все его точки совершат собственные элементарные перемещения. Рассмотрим две произвольные точки : j и k (рис. 14.11), положение которых определяют радиусы-векторы rj и rk. Элементарные перемещения этих точек будут drj и drk. Силы взаимодействия меж-ду точками любой пары, согласно III закону динамики, равны по модулю и противопо-ложны по направлению, т.е.:
Произвольное элементарное перемещение всего тела можно представить как геометрическая сумма поступательного и сферического перемещений. Тогда элементарное перемещение точки k будет равно:
| 
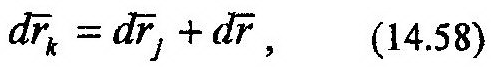где drj – элементарное перемещение точки k, соответ-ствующее поступательной составляющей перемещения всего тела;
dr – элементарное перемещение точки k, соответ-ствующее сферической составляющей перемещения всего тела.
|
Определим величину суммы работ внутренних сил взаимодействия указанных на рисунке точек. Воспользуемся для этого выражением (14.50), получим:
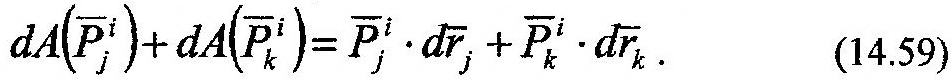
Произведем небольшие преобразования последнего слагаемого (14.59), учитывая (14.57) и (14.58), получим:
| Поскольку |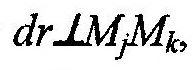 
| , постольку |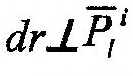 
| и |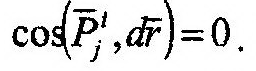 
| Тогда сумма элементар- |
ных работ, указанных на рис. 14.11, внутренних сил будет равна нулю:
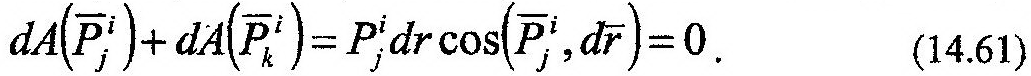
Так как каждой внутренней силе найдется такая же по величине, но противоположная по направлению другая внутренняя сила, то сумма элементарных работ всех внутренних сил твердого тела будет равна нулю, т.е.:
Аналогичный результат можно получить при определении суммы работ внутренних сил твердого тела, совершаемых на конечном перемещении. Действительно, работа силы на конечном перемещении можно представить как предел суммы элементарных работ.
| Поэтому: | 
|
или: сумма работ внутренних сил твердого тела на любом его перемещении равна ну-
Лю.
Дата добавления: 2016-04-19; просмотров: 597;