Можных перемещений.
Например, для свободной точки можно указать три независимых возможных перемещения (все три – линейные), а для свободного тела – шесть (три – линейные и три –
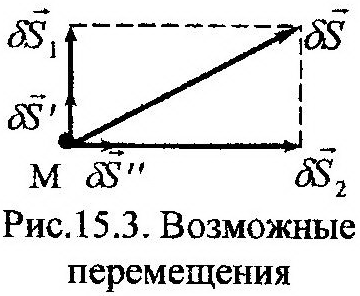
угловые). Все остальные возможные перемещения представ-ляют собой результат геометрического суммирования независи-мых перемещений. На рис. 15.3 приведен такой пример. Воз-можное перемещение мочки М, δS, можно представить как геометрическую сумму двух независимых перемещений δS’ и δS’’, модули которых изменены следующим образом:
 где k1, k2 – скалярные коэффициенты.
где k1, k2 – скалярные коэффициенты.
|
|
Введем понятие идеальной связи, реакция которой нормальна возможному перемеще-
| нию. Примером идеальной связи может служить гладкая наклон-ная поверхность, коэффициент трения которой равен нулю. В этом случае тело под действием силы тяжести может пе-ремещаться только по самой поверхности, и его возможное перемещение, δS, будет ориентировано нормально реакции поверхности, N (рис. 15.4). | 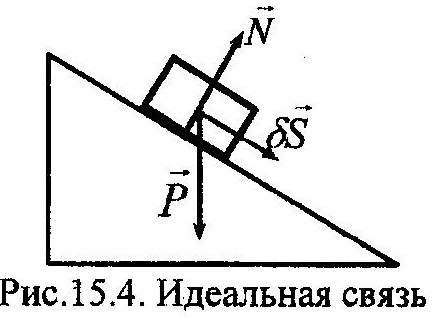
|
Введем понятие виртуальной работы, δА, как элементарной работы, совершаемой силой на возможном перемещении.
Обозначим виртуальную работу активной силы, δАа, и δАr.
Рассмотрим систему n материальных точек (рис. 15.5), которая под действием всех прило-женных к ней сил и связей находится в равновесии. Все связи системы будем считать идеальными. Тогда сумма виртуальных работ реакций этих связей будет:

Поскольку система находится в равновесии, постольку между главными векторами всех активных сил и сил реакций, приложенных к каждой точке, будет иметь место следующее соотношение:

Отсюда следует, что на любом возможном перемещении δSk сумма работ этих сил будет равна нулю, т.е.:

Аналогичные равенства могут быть записаны для любой точки механической системы. Сложив почленно все n уравнений вида (15.15), получим:
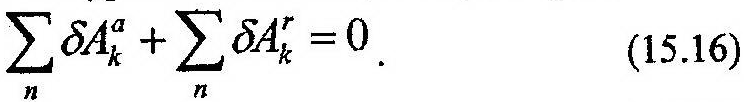
Если на систему будут наложены идеальные связи, то, с учетом (15.13), получим:

или:
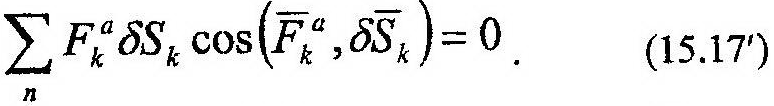
В аналитической форме выражение (15.17) будет иметь следующий вид:

где δxk, δyk, δzk – проекции возможного перемещения δSk на координатные оси.
| Таким образом, мы показали, что если система с идеаль-ными связями находится в равновесии, то имеет место ра-венство (15.17). Справедливо и обратное утверждение. Отсюда вытекает следующий принцип возможных перемещение (принцип Лагранжа): для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма виртуальных работ всех действующих на систему активных сил при любом возможном перемещении была равна нулю. | 
|
Дата добавления: 2016-04-19; просмотров: 644;
