ЛЕКЦИЯ 17. Общее уравнение динамики

Рассмотренные выше два принципа позволяют создать универсальный метод решения задач динамики механических систем. Действительно, принцип Даламбера при-

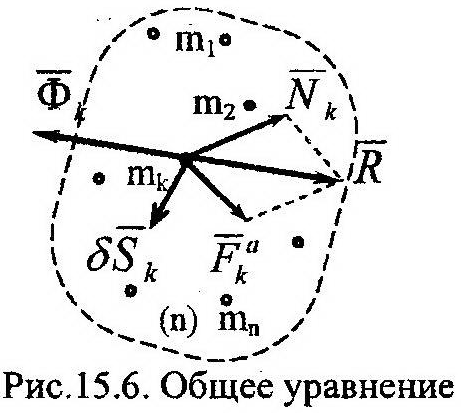
водит систему в равновесное состояние, а принцип Лагранжа предлагает общий метод решения задач статики. Рассмотрим систему n материальных точек (рис. 15.6), на которую наложены идеальные связи. Если ко всем точкам системы, кроме фактически действующих на них активных, Fa, и сил реакций, N, приложить силы инерции, Ф, то система придет в равновесное состояние и к ней можно будет применить принцип возможных перемещений. В результате получим:
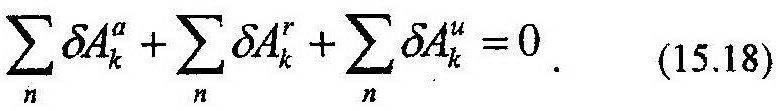
Учитывая, что на систему наложены идеальные связи, т.е.:		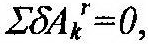выражение (15.18)

принимает следующий вид:

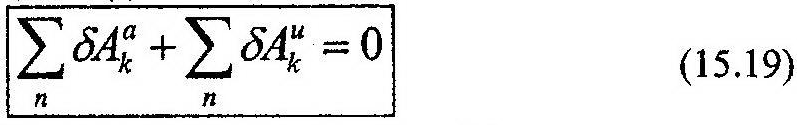
Это выражение и есть общее уравнение динамики. Из него вытекает принцип Лагранжа-Даламбера: при движении механической системы с идеальными связями в каждый момент времени сумма виртуальных работ всех приложенных активных и сил инерции на любом возможном перемещении системы будет равна нулю.

В аналитической форме уравнение (15.19) имеет следующий вид:

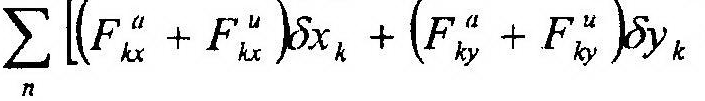
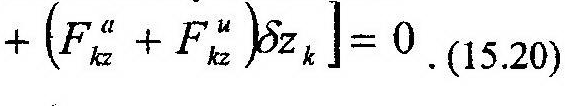
Уравнения (15.19) и (15.20) позволяют решать задачи динамики механических систем как материальных точек, так и тел.