Механической системы

Рассмотрим механическую систему, состоящую из n материальных точек (рис. 13.2). Для вывода данной теоремы воспользуемся системой дифференциальных уравнений (13.6). Сложим почленно эти уравнения, получим:

Последняя сумма в (14.19) равна нулю по 1-му свойству внутренних сил. Левую же часть можно преобразовать следующим образом:

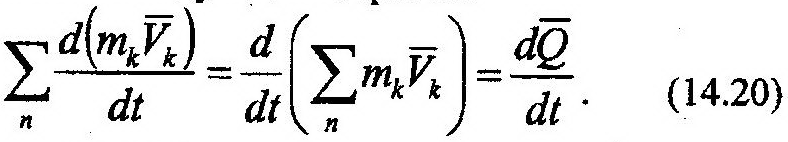
Учитывая (14.20), перепишем (14.19) в виде:

что и представляет собой векторную форму записи теоремы об изменении количества движения механической системы в дифференциальной форме, т.е.: производная по времени от количества движения механической системы равна геометрической сумме всех внешних сил, действующих на эту систему.

В скалярной форме эта теорема может быть записана в проекциях на координатные оси:

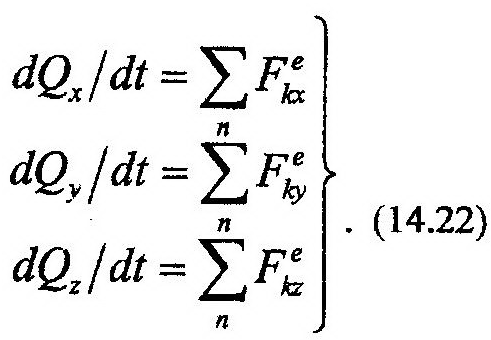
В конечном виде выражение теоремы можно получить как из выражения (14.21), так и из (14.22). Для этого необходимо разделить переменные и проинтегрировать эти выражения, получим:

или

 

где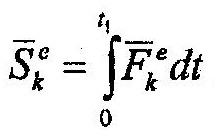

–импульс внешней k-й силы.

 

Саму теорему на основе (14.24) можно формулировать следующим образом:

Изменение количества движения механической системы за некоторый промежуток времени равно геометрической сумме импульсов внешних сил, действующих на систему, за тот же промежуток времени.

В скалярной форме выражение (14.24) можно получит, спроектировав его на координатные оси:

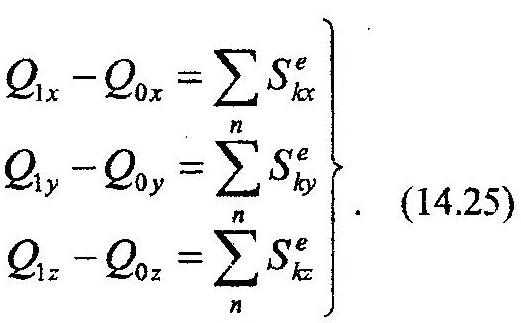
Преимуществом данной теоремы является то, что при ее использовании можно не учитывать внутренние силы, т.к они не способны изменить количество движения всей механической системы.

Частным случаем теоремы является закон сохранения количества движения механической системы,который может иметь место, когда:

1.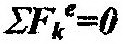

, тогда, согласно (14.21), имеем:

т.е. количество движения ме-

ханической системы не меняется со временем, когда геометрическая сумма внешних сил равна нулю.

2.

но, например,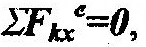

тогда, согласно (14.22) имеем: Qx=const – закон

сохранения имеет место относительно одной оси.