Ный центр на протяжении всего движения точки.
Наглядным примером такой силы является притяжение Солнцем любой планеты, в какой бы точке свой траектории она не находилась. При этом линия действия силы все время будет проходить через Солнце. Рассмотрим эту задачу в общем виде. Пусть на точку М действует центральная сила F, линия действия которой пересекает центр О (рис. 14.5). По-
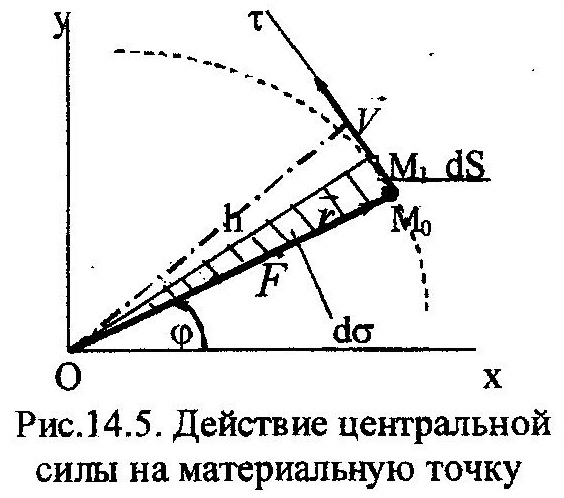
| ложение точки определяет радиус-вектор r. Правая часть выражения (14.32) равна нулю, поскольку данная сила создать момент относительно точки О не может. Поэтому:
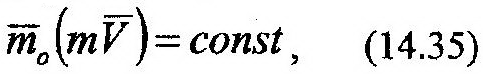 или
или
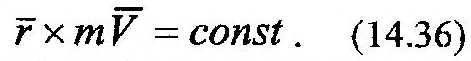 Полученный результат позволяет сделать следующие выводы. Поскольку вектор-момент количества движения точки не меняет свое направление в пространстве, по-
Полученный результат позволяет сделать следующие выводы. Поскольку вектор-момент количества движения точки не меняет свое направление в пространстве, по-
|
стольку два вектора, стоящие в левой части выражения (14.36) все время остаются в одной и той же плоскости (хОу – рис. 14.5). Это означает, что траектория точки будет являться плоской кривой. Постоянство модуля вектора-момента количества движения точки приводит к следующему:

| На рис. 14.5 видно, что | 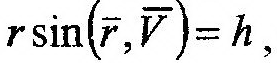
| тогда (14.37) можно переписать как: |
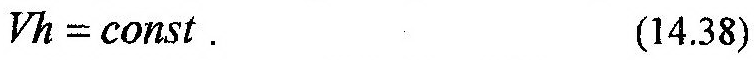
Учитывая, что скорость точки V=ds/dt, а dS*h=2dσ (где dσ – элементарная площадь сектора, заштрихованного на рис. 14.5), получим:

где dσ/dt – секторная скорость.
Подводя итоги рассмотренной задачи, можно сделать общий вывод о том, что:
Дата добавления: 2016-04-19; просмотров: 728;
