Ную геометрической сумме количеств движения всех точек данной системы,
| т.е.: | 
|
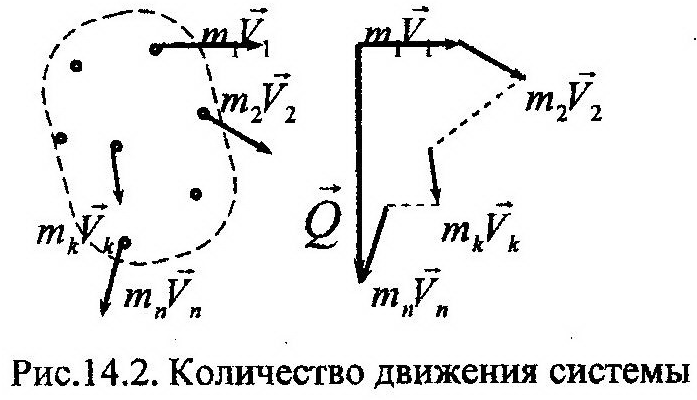
На рис. 14.2 показана система n материальных точек, каждая из которых имеет свою величину количества движения, mkVk. Построив из этих векторов многоугольник, можно найти вектор суммы, Q, который и является вектором количества движения механической системы. Ясно, что вектор суммы может принимать любые значения и быть равным нулю. Выражение (14.14) отражает сущность данной характеристики движения механической системы, но не может быть рекомендовано для ее определения. Действительно, если механическая система представляет собой совокупность большого числа точек, то процесс определения Q окажется весьма трудоемким. Найдем другую формулу этой величины. Для этого воспользуемся векторным выражением (13.3), определяющим положение центра масс механической системы. Умножим обе части этой формулы на массу системы, М, получим:

| Возьмем первую производную от обеих частей этого выражения. При этом учтем, что производная от суммы равна сумме производных, а масса точки и системы, как постоянные величины, могут быть вынесены за знак производной:
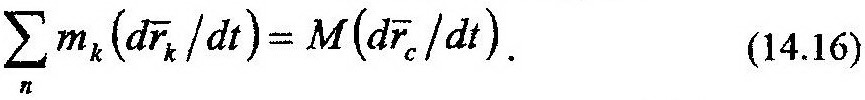
|
Производные от радиусов-векторов являются скоростями k-й точки и центра масс, поэтому выражение (14.16) перепишем в следующем виде:

Учитывая равенство правой части (14.14) и левой части (14.17), получим формулу для определения количества движения системы:

т.е.: количество движения механической системы равно произведению ее массы на
скорость центра масс.
Преимущество формулы (14.18) над выражением (14.14) очевидно, т.к. в (14.18) для определения Q требуется знать скорость только одной точки – центра масс. Интересно заметить, что в случае покоя этой точки, не зависимо от значений скоростей других точек системы, количество движения механической системы будет равно нулю. Таким образом,
количество движения – это характеристика поступательной составляющей движе-
Дата добавления: 2016-04-19; просмотров: 651;
