Движение центра масс механической системы
Найдем уравнение, описывающее движение характерной точки механической системы – ее центра масс. Для этого сложим почленно обе части уравнений (13.6), получим:
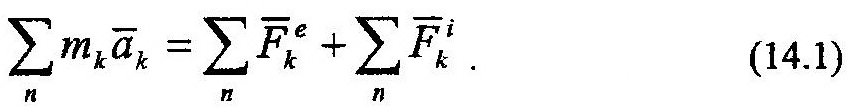
Преобразуем левую часть уравнения (14.1) с помощью выражения (13.3), определяющего положение центра масс системы.
Из (13.3) имеем:

Возьмем вторую производную от обеих частей (14.2), получим:
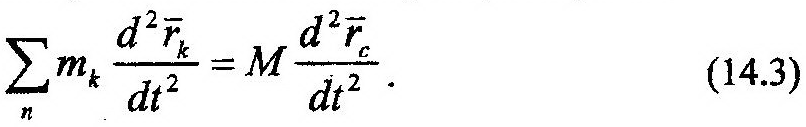
Учтем, что вторые производные от радиусов-векторов являются ускорениями соответствующих точек механической системы. Тогда выражение (14.3) перепишем в виде:

Учитывая, что левая часть (14.1) равна правой части (14.4), а также используя свойство 1 внутренних сил системы, получим уравнение движения центра масс:

Уравнение (14.5) выражает теорему о движении центра масс механической системы: произведение массы механической системы на ускорение ее центра равно геометрии-ческой сумме всех внешних сил, действующих на систему.
Механический смысл данной теоремывиден в следующей формулировке: центр масс механической системы движется как материальная точка, имеющая массу всей системы и подверженная воздействию всех внешних сил, приложенных к самой системе.
Кроме векторной формы записи теоремы можно для решения задач использовать скалярную. Для этого выражение (14.5) следует спроектировать на координатные оси. Получим:
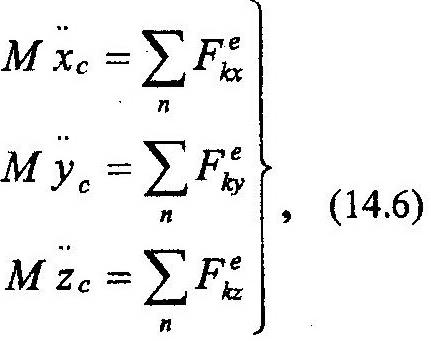
| где | 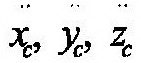
| – проекции ускорения центра масс на координатные оси. |
Практическое значение теоремы о движении центра масс состоит в следующем:
1. Теорема дает теоретическое обоснование методам динамики точки. Из (14.5) видно, что
результаты решения задачи о движении тела, представленного в виде материальной точки, относятся к конкретной точке тела – центру масс.
2. Решение задач на основе выражений (14.5) и (14.6) позволяет исключить из рассмотре-
ния внутренние силы системы. Это означает, что действие внутренних сил не влияет на движение центра масс механической системы.
Частным случаем записи выражений (14.5) или (14.6) является равенство нулю их правых частей. В этих случаях имеет место
Дата добавления: 2016-04-19; просмотров: 1294;
