Теорема об изменении кинетического момента
Для вывода теоремы об изменении кинетического момента механической системы воспользуемся выражением (14.33), отражающим изменение момента количества движения точки. Механическую систему представим как совокупность n материальных точек (рис. 14.2). При этом классифицируем все силы на внешние и внутренние. Для произвольной k-й точки правая часть выражения (14.33) примет следующий вид:
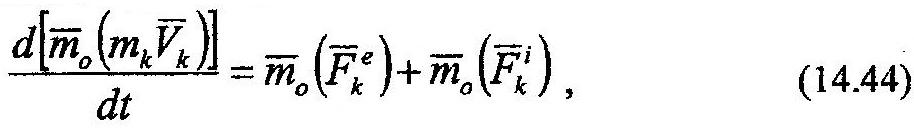
| где | 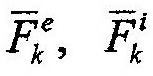
| – равнодействующие внешних и внутренних сил, приложенных к данной точке. |
Для каждой точки механической системы можно составить выражение (14.44), где индекс k примет свое значение, соответствующее номеру точки (k=1…n). Таким образом получим систему, состоящую из n дифференциальных уравнений вида (14.44). Сложим почленно эти уравнения, получим:
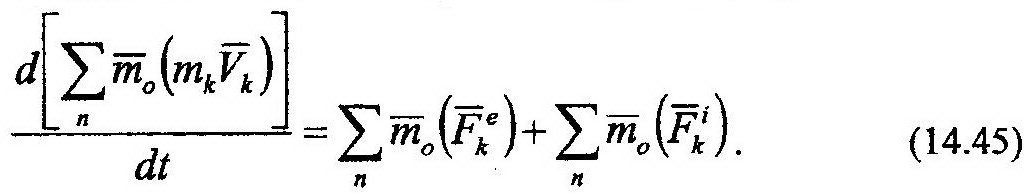
Согласно второму свойству внутренних сил механической системы последнее слагаемое (14.45) равно нулю, а в левой части, под знаком дифференциала, имеем выражение кинетического момента (14.40). С учетом этого выражение (14.45) можно переписать в виде:
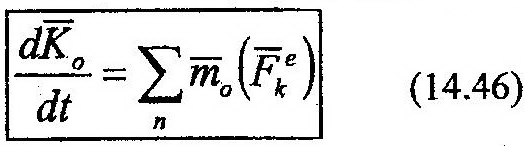
что и отражает теорему об изменении кинетического момента механической системы, а именно: производная по времени от кинетического момента механической системы, определенного относительно произвольного неподвижного центра, равна геометрической сумме моментов всех внешних сил относительно того же центра.
Проектируя (14.46) на координатные оси, получим выражение теоремы в скалярной форме записи. Например, на ось х:
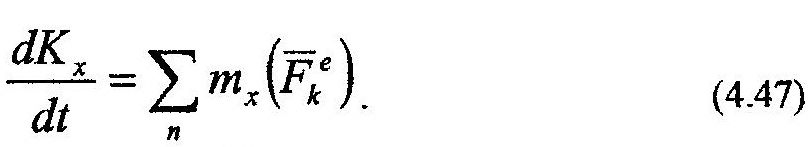
Практическая ценность этих выражений заключается в том, что при их использовании нет необходимости учитывать внутренние силы системы.
Частным случаем доказанной теоремы является закон сохранения кинетического момента механической системы, который может иметь место, когда:
| 1. | 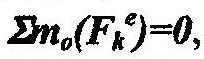
| , тогда K0=const, т.е. кинетический момент системы не изменяется со вре- |
менем ни по величине, ни по направлению.
| 2. | 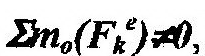
| но сумма проекций внешних сил на какую-либо из осей равна нулю, на- | ||
| пример, | 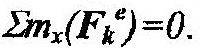
| Тогда: Kх=const, т.е. кинетический момент системы сохраня- | ||
ет свое значение относительно данной оси.
Дата добавления: 2016-04-19; просмотров: 894;
