Момент равнодействующей плоской ССС относительно любого центра, лежащего в той же плоскости, равен алгебраической сумме моментов слагаемых сил относительно того же центра.
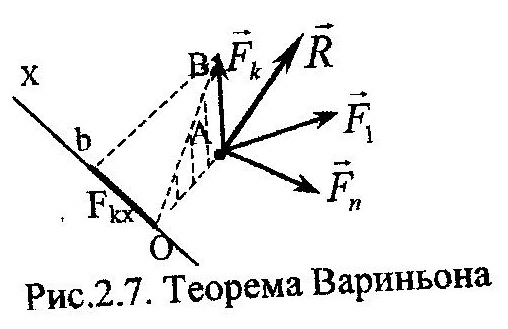
| Рассмотрим ССС (F1…Fn), линии действия которых пересекаются в точке А. Воспользуемся следствием 2-й аксиомы и приложим их в этой точке (рис. 2.7). Пусть сила R является равнодействующей данной системы сил, т.е.:

|
Соединим точку А с центром О и проведем ось Ох перпендикулярно отрезку ОА. Положительное направление оси зададим таким образом, чтобы знаки проекции любой силы на эту ось и ее момента относительно точки О совпадали. На основании свойства 3 момента силы, можно записать для произвольной силы Fk следующее:

но, с другой стороны, удвоенная площадь ΔОАВ может быть определена как:
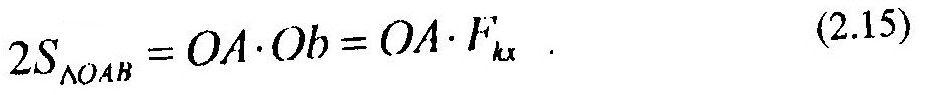
Следовательно,

Спроектируем обе части (2.13) на ось х и умножим их на постоянную величину ОА, получим:
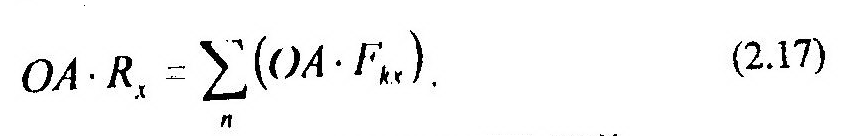
Сравнивая обе части (2.17) с (2.16), приходим к выводу, что:
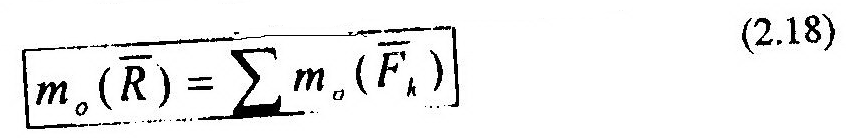
что и требовалось доказать.
Формула (2.18) является математическим выражением теоремы Вариньона.
Следует заметить, что данную теорему можно использовать не только к системе сил, но и к любой системе векторов, о чем мы убедимся в следующих разделах.
Пара сил
Дата добавления: 2016-04-19; просмотров: 639;
