Центра, лежащего в ее плоскости действия, не зависит от положения центра и равна моменту пары.

Пусть дана пара сил (F, F’)и произвольно выбранный центр О. Расстояние от центра до линий действия сил и плечо пары показано на рис. 3.4. Определим сумму моментов сил пары относительно точки О: 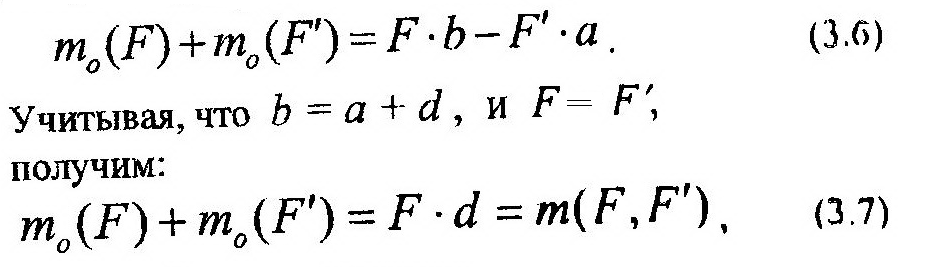что и требовалось доказать.

Момент силы относительно центра как вектор

При рассмотрении плоской системы сил плоскость действия момента определена заранее. В случае же пространственной системы сил плоскость действия каждого момента необходимо определить геометрически, что приведет к дополнительным графическим построениям. Избежать это можно представляя момент как вектор Мо (рис. 5.1). Правило представления вектора-момента: момент силы относительно центра изображается векторомМо,

Приложенным к центру О и направленным нормально плоскости, задаваемой вектором силы F и центром О, в ту сторону, откуда видится вращение вектора силы относительно центра против хода часовой стрелки.

В векторной записи момент силы можно определить по формуле:

где r – радиус-вектор точки приложения силы (рис. 5.1);

x, y, z – координаты этой же точки.